В слое пористой среды движение жидкости описывается уравнением Дарси [1] и уравнением неразрывности, а в свободном слое - уравнением Эйлера, а также уравнением неразрывности. Записываются граничные условия на поверхностях раздела: на свободной поверхности жидкости, на поверхности раздела жидкость - пористая среда, а также на твердом дне, ограничивающем пористую среду, и боковых поверхностях сосуда.
Система координат выбирается так, что ось Oz направлена вертикально вверх против вектора ускорения свободного падения, а оси Ox и Oy лежат на плоской поверхности раздела жидкости и пористой среды и направлены вдоль двух боковых поверхностей сосуда.
Математическая модель рассматриваемой задачи состоит из дифференциальных уравнений в частных производных второго порядка и кинематических и динамических условий на поверхностях раздела для нахождения неизвестных функций, которые ищутся в виде стоячих затухающих волн:
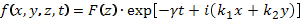 , где
, где ![]() .
.
Приведен анализ полученного решения. Подробно рассматриваются различные частные случаи. В предельном случае неограниченной поверхности жидкости, полученные результаты переходят в результаты работы [2].
Автор благодарит профессора Н. Г. Тактарова за руководство работой.
СПИСОК ЛИТЕРАТУРЫ:
- Гершуни Г. З., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости. - М.: Наука, 1972. - 392 с.
- Столяров И. В., Тактаров Н. Г. Распространение поверхностных волн в слое жидкости на пористом основании // Изв. АН СССР, МЖГ. - 1987. - №5. С. 183-186.
Библиографическая ссылка
Миронова С.М. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СТОЯЧИХ ВОЛН В СЛОЕ ЖИДКОСТИ НА ПОРИСТОМ ОСНОВАНИИ В СОСУДЕ, ИМЕЮЩЕМ ФОРМУ ПАРАЛЛЕЛЕПИПЕДА // Современные наукоемкие технологии. 2010. № 4. С. 61-62;URL: https://top-technologies.ru/ru/article/view?id=24640 (дата обращения: 05.03.2026).



