Чтобы определить зависимость частоты света v от скорости v, рассмотрим распространение света от двух источников, один из которых S движется по направлению к приемнику со скоростью v, а другой S0 покоится. Одинаковые источники излучают свет одинаковой частоты v0 (рис. 1). Свет относительно источников распространяется с одинаковой скоростью с, поэтому и длина излучаемой волны λ будет одинакова.
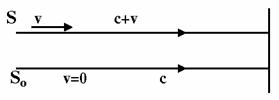
Рис. 1
Для приемника света периоды колебаний в световой волне от движущегося и покоящегося источников будут равны соответственно:
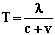
и
.
Периоды есть величины обратные частотам колебаний
и
.
Подставляем эти значения Т и Т0 в полученные равенства и делим почленно
и
;
;
(после сокращения на λ).
Для случая, когда источник света удаляется от приемника, следует знак перед v заменить на противоположный и получим:
.
Отметим, что c+v и с это скорости света соответственно относительно приемника и источника света.
Рассмотрим случай, когда источник света движется перпендикулярно направлению на приемник. Учитывая, что свет связан с источником, распространяется относительно его со скоростью с и сносится с ним со скоростью v, чтобы он попал на приемник, его надо направить под некоторым углом α так, что
(рис. 2). В этом случае составляющая скорости света, совпадающая с направлением на приемник А будет 
, составляющая v на это направление равна 0.
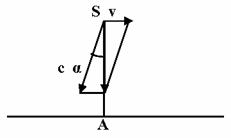
Рис. 2
Чтобы не повторять предыдущие рассуждения, воспользуемся формулой
,
c+v заменим на 
, а скорость с относительно источника останется неизменной. В результате получаем
,
что соответствует результату, полученному в опытах Айвса.
Ранее мы использовали понятие светонесущей среды, которая имеется у атомов источника света, но атом источника может быть и атомом приемника света. Можно считать, что и приемник света имеет светонесущую среду, которая распространяется неограниченно и в которой свет распространяется со скоростью равной с=3∙108 м/с.
Не исключена возможность того, что этой средой приемник перехватывает свет на некотором расстоянии от осязаемого приемника света. Применим это для объяснения эффекта Доплера (рис. 3).
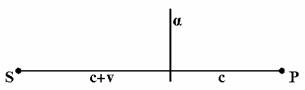
Рис. 3
Пусть S - источник света, Р - приемник, α - граница раздела светонесущих сред. Источник и приемник сближаются со скоростью v. Тогда для приемника свет от S до α будет иметь скорость c+v, а от α до Р скорость будет с. Источник испускает свет, длина волны которого и частота соответственно равны λ0 и ν0 , а скорость с, поэтому имеем
.
Для приемника λ0 пройдет границу α за время
.
Пройдя границу каждый элемент волны будет иметь скорость относительно приемника с и пройдет расстояние
.
Выражаем λ и λ0 через частоты ν и ν0
отсюда
.
Получили, что при сближении источника и приемника света
,
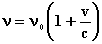а при удалении
Для поперечного эффекта Доплера скорость света относительно приемника равна , время прохождения длины λ0 через границу α
,
а длина волны после прохождения границы будет
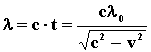
Аналогично предыдущему случаю получаем
Если факт перехвата света светонесущей средой приемника имеет место, то положение границы раздела светонесущих сред источника и приемника света может быть обнаружен в опытах с движущимся источником света.
СПИСОК ЛИТЕРАТУРЫ
- Зисман Г.А., Тодес О.М. Курс общей физики т.3, 1972 г., «Наука».
- Воронцов-Вельяминов Б.А. Астрономия 10, 1983 г., «Просвещение».
Библиографическая ссылка
Дегтярева Е.Р., Юшкевич Р.С., Куликова И.Ю. ЭФФЕКТ ДОПЛЕРА // Современные наукоемкие технологии. – 2010. – № 4. – С. 34-37;URL: https://top-technologies.ru/ru/article/view?id=24626 (дата обращения: 21.11.2024).