Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

Балданова Д.М. Балданов М.М. Танганов Б.Б.

Показывается возможность получения уравнения Шредингера в различных условиях в координатах Эйлера.

Статья в формате PDF

133 KB

уравнение Шредингера

координаты Эйлера

оператор Гамильтона

волновая функция

equation of Shredinger

coordinates of Eiler

operator of Gamilton

wave function

,

где q (x,y,z)- координата; ψ - волновая функция;  - импульс, в котором S есть функция действия; E - энергия.

Далее им приведено уравнение в виде:

.  (1)

Это уравнение сам Э. Шредингер называет [1, С.626] эйлеровским дифференциальным уравнением. Никаких комментариев и ссылок по этому поводу он не приводит. Введение Э. Шредингером в уравнение (1) вместо постоянной К величины 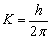 позволило получить уравнение вида:

.   (2)

В таком виде уравнение (2) называют стационарным уравнением Шредингера.

Как видно, основой приведенного уравнения (1) является волновая функция

ψ (t,p,g),

где t,p,g можно назвать координатами Эйлера: t - время или временной масштаб события, q(x,y.z) - пространственный масштаб и p(p_x,p_y,p_z) - импульс или энергетический эффект, сопровождающий данное явление.

В настоящем сообщении рассматривается возможность получения различных вариантов уравнения Шредингера в зависимости от бесконечно малого изменения волновой функции ψ(t,p,g) в форме ее дифференциала:

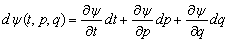.  (3)

Откуда следует, что

.     (4)

Из курса механики известно, что:

 - скорость;

 - сила,

где Н - функция Гамильтона, равная , в которой U - потенциальная энергия. Учитывая данные выражения, уравнение (4) можно записать в виде:

.  (5)

Также из курса механики известно выражение, которое представляет собой классическую скобку Пуассона:

,

Следовательно, выражение (5) можно представить в упрощенном виде:

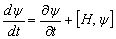.    (6)

Если волновая функция ψ не зависит явно от времени, т.е. 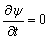, в этом случае, дальнейшее упрощение выражения (6) приводит к виду:

.  (7)

Введение же в приведенное выражение (7) оператора Гамильтона  вместо функции Гамильтона H дает возможность получения упрощенного уравнения Шредингера в виде:

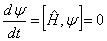, (8)

а это есть, по-существу, стационарное уравнение Шредингера.

Как показано, оператор Гамильтона H^ определяется операторами импульса p^ и U(q^). Следовательно, возникает необходимость установления видов p^ и q^. Обычно, во многих изданиях по квантовой механике эти величины постулируются, т.е. даются без выводов и доказательств. Для решения данной задачи можно использовать для волновой функции ψ(t,p,g), так называемые Фурье - преобразования [2, С.630-631]:

; (9)

.  (10)

Дифференциалы левых и правых частей уравнений (9) и (10) позволяет устранить непростые интегралы в правых частях данных равенств:

;  (11)

.   (12)

Дифференцирование уравнения (11) по импульсу p и уравнения (12) по координате q приводит к следующим равенствам:

;(13)

.  (14)

Полученные выражения с учетом уравнений (11) и (12) можно представить в упрощенных формах:

;(15)

.  (16)

Отсюда следует, что

; (17)

.   (18)

Далее, в правую часть выражений (17) и (18) введем обозначения q = q^ и p = p^ соответственно. Это и есть искомые операторы импульса и координаты, которые называют эрмитовыми [4, C.42, 63]:

; (19)

.  (20)

Следовательно, оператор Гамильтона в уравнении (8) имеет вид:

.  (21)

Отсюда вытекает условие эрмитовости [4, C.42, 63]:

. (22)

Данное выражение показывает, что результат дифференцирования функций по двум различным переменным не зависит от порядка дифференцирования, или иначе функции φ и ψ коммутативны [3, C.67, 73]:

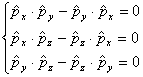.  (23)

Тогда как координата и соответствующая ей составляющая импульса не коммутируют в отличие от выражения (23):

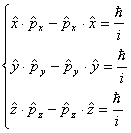.  (24)

Так же, значение оператора Гамильтона H^ позволяет перейти к так называемым перестановочным соотношениям Иордана-Борна. Так, согласно Дираку [1, C.617], разность гейзенберговских произведений двух квантовых величин х и у равна скобке Пуассона этих величин, умноженной на :

                                    (25)

Теперь, если же волновая функция ψ зависит явно от времени, т.е. , то получаем нестационарное уравнение Шредингера:

.   (26)

Далее использование скобки Пуассона из перестановочного соотношения Иордана-Борна (25) в полученном уравнении позволяет получить выражение (26) в виде:

.   (27)

Согласно Дираку [5. С.37], поскольку уравнение (27) содержит два неизвестных, то оно не имеет решения даже для атома водорода. В последующие годы при изучении уравнения (27) физики нашли способ решения в виде двух задач:

1. Первая колебательная задача состоит в постулировании содержания волновой функции ψ и использовании матрицы силовых полей, дающих экспериментально энергии;
2. Вторая задача состоит в постулировании энергии и дальнейшем нахождении функции ψ.

Использование в первой колебательной задаче волновой функции Слейтера-Зинера и потенциалов ионизаций атомов ионов позволило нам теоретически рассчитать ионные радиусы элементов в хорошем соответствии с эмпирически и полуэмпирическими значениями радиусов ионов по Полингу, Гольдшмидту Белову-Бокию, Мелвину-Хьюзу и Ингольду [6].

СПИСОК ЛИТЕРАТУРЫ

1. Успехи физических наук. - М.: Наука. - 1977. - Т. 122. - Вып. 4. - С. 561-623, 625, 574, 611, 621.
2. Блохинцев Д.И. Основы квантовой механики. - М.: Наука. - 1976. - 664 с.
3. Шпольский Э.В. Атомная физика: учебное пособие. - М.: Наука. - 1984. - Т. 2. - 440 с.
4. Ландау Л.Д., Лифшиц Е.М. Квантовая механика (нерелятивистская теория). - М.: Наука. - 1989. - Т.3 - 768 с.
5. Дирак П.А.М. Пути физики / Под. Ред. Г. Хора, Дж. Шепанского. - М.: Энергоатомиздат. - 1983. - 88 с.
6. Балданов М.М., Балданова Д.М., Жигжитова С.Б., Танганов Б.Б. Константа экранирования Слейтора-Зинера и радиусы одноатомных ионов // Известия вузов. Физика.- 2006.- Т. 49. - №3.- С.59-67.

Библиографическая ссылка