У каждого алгоритма есть свои преимущества и недостатки. Поэтому важно выбрать тот алгоритм, который лучше всего подходит для решения конкретной задачи.
Задачу поиска можно сформулиро-вать так: найти один или несколько элементов в множестве, причем искомые элементы должны обладать определенным свойством. Это свойство может быть абсолютным или относительным. Относительное свойство характеризует элемент по отношению к другим элементам: например, минимальный элемент в множестве чисел. Пример задачи поиска элемента с абсолютным свойством: найти в конечном множестве занумерованных элементов элемент с номером 13, если такой существует.
Таким образом, в задаче поиска имеются следующие шаги [2]:
1) вычисление свойства элемента; часто это - просто получение «значения» элемента, ключа элемента и т. д.;
2) сравнение свойства элемента с эталонным свойством (для абсолютных свойств) или сравнение свойств двух элементов (для относительных свойств);
3) перебор элементов множества, т. е. прохождение по элементам множества.
Первые два шага относительно просты. Вся суть различных методов поиска сосредоточена в методах перебора, в стратегии поиска и здесь возникает ряд вопросов [2]:
- Как сделать так, чтобы проверять не все элементы?
- Если же задача требует неоднократного прохода по всем элементам множества, то как уменьшить количество проходов?
Ответы на эти вопросы зависят от структуры данных, в которой хранится множество элементов. Накладывая незначительные ограничения на структуру исходных данных, можно получить множество разнообразных стратегий поиска различной степени эффективности.
Последовательный поиск
Поиск нужной записи в неотсортированном списке сводится к просмотру всего списка до того, как запись будет найдена. "Начать с начала и продолжать, пока не будет найден искомый ключ, затем остановиться" [1] -это простейший из алгоритмов поиска. Этот алгоритм не очень эффективен, однако он работает на произвольном списке.
Перед алгоритмом поиска стоит важная задача определения местонахож-дения ключа, поэтому он возвращает индекс записи, содержащей нужный ключ. Если поиск завершился неудачей (ключевое значение не найдено), то алгоритм поиска обычно возвращает значение индекса, превышающее верхнюю границу массива.
Здесь и далее предполагается, что массив А состоит из записей, и его описание и задание произведено вне процедуры (массив является глобальным по отношению к процедуре). Единственное, что требуется знать о типе записей - это то, что в состав записи входит поле key - ключ, по которому и производится поиск. Записи идут в массиве последовательно и между ними нет промежутков. Номера записей идут от 1 до n - полного числа записей. Это позволит нам возвращать 0 в случае, если целевой элемент отсутствует в списке. Для простоты мы предполагаем, что ключевые значения не повторяются.
Процедура SequentialSearch выпол-няет последовательный поиск элемента z в массиве A[1..n].
SequentialSearch(A, z, n)
(1) for i ←1 to n
(2) do if z = A[i].key
(3) then return i
(4) return 0
Анализ наихудшего случая. У алгоритма последовательного поиска два наихудших случая. В первом случае целевой элемент стоит в списке последним. Во втором его вовсе нет в списке. В обоих случаях алгоритм выполнит n сравнений, где n - число элементов в списке.
Анализ среднего случая. Целевое значение может занимать одно из n возможных положений. Будем предполагать, что все эти положения равновероятны, т. е. вероятность встретить каждое из них равна 
. Следовательно, для нахождения i‑го элемента A[i] требуется i сравнений. В результате для сложности в среднем случае мы получаем равенство
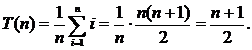
Если целевое значение может не оказаться в списке, то количество возможностей возрастает до n + 1. при отсутствии элемента в списке его поиск требует n сравнений. Если предположить, что все n + 1 возможностей равновероятны, то получим
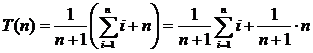
Получается, что возможность отсутствия элемента в списке увеличивает сложность среднего случая на 
, но по сравнению с длиной списка, которая может быть очень велика, эта величина пренебрежимо мала.
Рассмотрим общий случай, когда вероятность встретить искомый элемент в списке равна pi , где pi ≥ 0 и 
В этом случае средняя сложность (математическое ожидание) поиска элемента будет равна 
Хорошим приближением распределения частот к действительности является закон Зипфа: 
для i = 1, 2, ..., n. [n‑е наиболее употребительное в тексте на естественном языке слово встречается с частотой, приблизительно обратно пропорциональной n.] Нормирующая константа выбирается так, что Пусть элементы массива A упорядочены согласно указанным частотам, тогда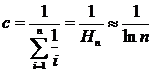 
и среднее время успешного поиска составит
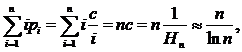что намного меньше 
. Это говорит о том, что даже простой последовательный поиск требует выбора разумной структуры данных множества, который бы повышал эффективность работы алгоритма.
Алгоритм последовательного поиска данных одинаково эффективно выполня-ется при размещении множества a1, a2,..., an на смежной или связной памяти. Сложность алгоритма линейна - O(n).
Логарифмический поиск
Логарифмический (бинарный или метод делением пополам) поиск данных применим к сортированному множеству элементов a1 < a2 < ... < an, размещение которого выполнено на смежной памяти. Суть данного метода заключается в следующем: поиск начинается со среднего элемента. При сравнении целевого значения со средним элементом отсортированного списка возможен один из трех результатов: значения равны, целевое значение меньше элемента списка, либо целевое значение больше элемента списка. В первом, и наилучшем, случае поиск завершен. В остальных двух случаях мы можем отбросить половину списка. Действительно, когда целевое значение меньше среднего элемента, мы знаем, что если оно имеется в списке, то находится перед этим средним элементом. Если целевое значение больше среднего элемента, мы знаем, что если оно имеется в списке, то находится после этого среднего элемента. Этого достаточно, чтобы мы могли одним сравнением отбросить половину списка.
Итак, результат сравнения позволяет определить, в какой половине списка продолжить поиск, применяя к ней ту же процедуру.
Процедура BinarySearch выполняет бинарный поиск элемента z в отсортированном массиве A[1..n].
BinarySearch(A, z, n)
(1) p←1
(2) r←n
(3) while p ≤ r do
(4) q← [(p+r)/2]
(5) if A[q].key = z
(6) then return q
(7) else if A[q].key < z
(8) then p←q+1
(9) else r←q-1
(10) return 0
Анализ наихудшего случая. Поскольку алгоритм всякий раз делит список пополам, будем предполагать при анализе, что n = 2k ‑ 1 для некоторого k. Ясно, что на некотором проходе цикл имеет дело со списком из 2j ‑ 1 элементов. Последняя итерация цикла производится, когда размер оставшейся части становится равным 1, а это происходит при j = 1 (так как 21 ‑ 1 = 1). Это означает, что при n = 2k ‑ 1 число проходов не превышает k. Следовательно, в наихудшем случае число проходов равно k = log2(n+1).
Анализ среднего случая. Рассмотрим два случая. В первом случае целевое значение наверняка содержится в списке, а во втором его может там и не быть. В первом случае у целевого значения n возможных положений. Будем считать, что все они равновероятны. Представим данные a1 < a2 < ... < an в виде бинарного дерева сравнений, которое отвечает бинарному поиску. Бинарное дерево называется деревом сравнений, если для любой его вершины выполняется условие:
{Вершины левого поддерева} < {Вершина корня} < {Вершины правого поддерева}
Если рассматривать бинарное дерево сравнений, то для элементов в узлах уровня i требуется i сравнений. Так как на уровне i имеется 2i‑1 узел, и при n = 2k ‑ 1 в дереве k уровней, то полное число сравнений для всех возможных случаев можно подсчитать, просумми-ровав произведение числа узлов на каждом уровне на число сравнений на этом уровне.
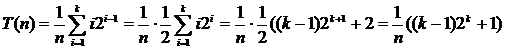
Подставляя 2k = n + 1, получим
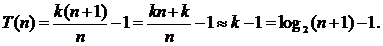
Во втором случае число возможных положений элемента в списке по-прежнему равно n, однако на этот раз есть еще n + 1 возможностей для целевого значения не из списка. Число возможностей равно n + 1, поскольку целевое значение может быть меньше первого элемента в списке, больше первого, но меньше второго, больше второго, но меньше третьего, и так далее, вплоть до возможности того, что целевое значение больше n‑го элемента. В каждом из этих случаев отсутствие элемента в списке обнаруживается после k сравнений. Всего в вычислении участвует 2n + 1 возможностей.
.
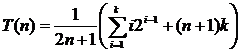Аналогично получаем, что
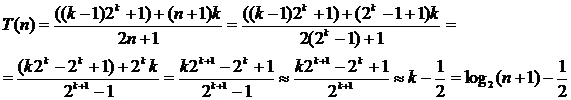
Значит, сложность поиска является логарифмической O(log2n).
Рассмотренный метод бинарного поиска предназначен главным образом для сортированных элементов a1 < a2 < ... < an на смежной памяти фиксированного размера. Если же размерность вектора динамически меняется, то экономия от использования бинарного поиска не покроет затрат на поддержание упорядо-ченного расположения a1 < a2 < ... < an.
СПИСОК ЛИТЕРАТУРЫ:
- Кнут, Д. Искусство программирования. Т. 3. Сортировка и поиск. - М.: Издательский дом «Вильямс», 2003.
- Королев, Л. Н. Информатика. Введение в компьютерные науки / Л. Н. Королев, А. И. Миков. - М.: Высш. шк., 2003.
Библиографическая ссылка
Ахтамова С.С. АЛГОРИТМЫ ПОИСКА ДАННЫХ // Современные наукоемкие технологии. – 2007. – № 3. – С. 11-14;URL: https://top-technologies.ru/ru/article/view?id=24620 (дата обращения: 21.11.2024).