Кривые линии постоянных чисел Маха для области свободного расширения сходятся в кромке сопла и почти прямолинейны на участке от кромки сопла до участка поворота в сторону оси сопла. Влияние спутного потока сказывается лишь на граничной линии, внутри области свободного расширения влияние спутного потока сказывается мало.
Для полного решения задачи по такой схеме достаточно задать распределение чисел Маха вдоль оси течения х и указать уравнение кривой, представляющей собой геометрическое место точек излома линии постоянных чисел М.
Так как в области течения разряжения типа центрированной волны имеется течение, аналогичное течению Прандтля - Майера в плоском случае, то линию излома можно определить как граничную характеристику второго семейства, отделяющую эту область от области расширения.
Ввиду того, что в области свободного расширения поток можно считать приближенно одноразмерным, то уравнение этой граничной характеристики определится по уравнению.
![]() , где
, где ![]() .
.
В случае равномерного распределения параметров в выходном сечении сопла эта линия должна проходить через точку r = 0, x = y.
В таком случае вдоль этой характеристики условие для определения x запишется так:
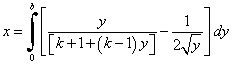
Интегрируя последнее уравнение, получим уравнение для определения зависимости М от х вдоль линии r =1.
Библиографическая ссылка
Исаев Ю.М., Николаев А.Г., Джабраилов Т.А. РАСЧЕТ ПОТОКА В ОБЛАСТИ СВОБОДНОГО РАСШИРЕНИЯ // Современные наукоемкие технологии. 2010. № 2. С. 43-43;URL: https://top-technologies.ru/ru/article/view?id=24444 (дата обращения: 13.03.2026).



