Задача рационального программно-целевого управления сложными техническими системами чрезвычайно актуальна для сельского хозяйства. Подтверждением этому является следующее: если по первой части научно-технического прогресса, связанного с созданием технических систем, в лучшем случае, можно добиться результатов, которые на десятки процентов (по потребительским свойствам) превосходят аналог, то за счет неэффективного управления мы теряем гораздо больше. Любая техническая система может быть использована с плюсом или с нулевым результатом, а эти два события отличаются друг от друга в бесконечное число раз.
Более того, в большинстве технологий, которые используются с отрицательным результатом, до сих пор отрицательный результат перекрывается дешевой рабочей силой, природной рентой и бюджетными дотациями. Переход из ситуации выработки управленческих решений в условиях неопределенности в условия выработки решений с вероятностным риском является, по нашему мнению, единственным.
Повышение эффективности производственных процессов растениеводства возможно двумя путями: совершенствованием методов и средств экспериментирования; развитием соответствующих идей и концепций. Первый подход связан с описанием изучаемого объекта, второй - с попыткой объяснения его сущности. Для осуществления второго подхода необходимо соотнести описание реакции производственной системы в целом с описаниями других явлений, которые свойственны более низким уровням этой организационной иерархии: общая модель производственного процесса, локальная модель (структурное подразделение), динамическая модель машинно-тракторного агрегата.
На основании общей модели производственного процесса:
,
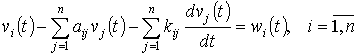где vi - производственный i-продукт; vj - производственный j-продукт; kij - коэффициент удельных капиталовложений; wi - интенсивность потребления, возможна оптимизация производственных процессов растениеводства в среднемноголетних условиях их функционирования (оптимизация стратегии), но адаптация этой модели к изменяющимся погодно-производственным ситуациям требует более детального математического описания.
Локальная модель производственного процесса:
,
где x - множество переменных состояния производственного процесса; u - множество всех значений управления производственным процессом; τ - множество погодно-производственных ситуаций (возмущений), определяет алгоритм поиска при наличии помех, позволяет оптимально достигать главной конечной цели производства (максимума прибыли) на каждом этапе функционирования системы с соблюдением множества ограничений (информационных, вычислительных и др.).
Адаптированная к складывающимся погодным ситуациям одномассная динамическая модель машинно-тракторного агрегата, полученная приведением сил и масс из уравнения движения в форме интеграла энергии:
,
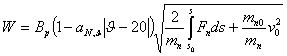где W - часовая производительность агрегата; Bp - рабочая ширина захвата агрегата; a N,u - коэффициент, характеризующий относительное уменьшение максимальной тяговой мощности трактора при изменении влажности почвы (вследствие изменения сопротивления) против нормативной на 1%; u - влажность почвы;mn - приведенная масса агрегата; s - значение обобщенной координаты агрегата; Fn - значение приведенной силы агрегата; v - модуль скорости точки приведения агрегата, позволяет учитывать изменение влажности почвы при установлении производительностей полевых механизированных работ.
Оптимизация механизированных производственных процессов по условиям функционирования в растениеводстве сводится к решению задачи вида
где Q - экстремизируемые функционалы; Θ - условия функционирования производственной системы; A - структура производственного процесса; X - исследуемые технико-технологические параметры; fi(X) - ограничения.
Цель поставленной задачи определяют критерии оптимизации и структура ограничений. Два контура оптимизации соответствуют двум видам оптимизации - параметрической (по X) и структурной (по A).
Структурная оптимизация состоит из трех этапов.
1 - составление таблиц испытаний. Выбирают N пробных точек α1,...,αN, равномерно расположенных в подмножестве А. В каждой из точек αi вычисляются все локальные критерии QV(αi). По каждому критерию составляется таблица испытаний, в которой значения 
расположены в порядке возрастания 
, где 
- номера соответствующих пробных точек (номера испытаний для каждого значения v).
2 - выбор критериальных ограничений. Рассматривая поочередно каждую из таблиц, при этом необходимо назначить ограничения QV** Исследователь заинтересован в уменьшении этих значений, но если выбирать все QV** слишком малыми, то множество допустимых точек Е может оказаться пустым. Анализ таблиц испытаний проводится для обоснованного выбора решающего критерия Q(α), так как позволяет учесть не только предварительные указания о роли отдельных критериев QV(α), но и их действительные возможности.
3 - проверка разрешимости задачи. Фиксируют какой-либо из критериев, например Qv1(α), и рассматривают соответствующую ему таблицу. Путем перебора имеющихся значений Qv(α) при всех значениях v нетрудно проверить, есть ли среди точек αi1,..., αis хотя бы одна такая, для которой справедливы одновременно все неравенства 
. Если такая точка есть, то множество Е непусто, и задача разрешима. В противном случае следует вернуться ко второму этапу и ослабить ограничение . Если такой шаг крайне нежелателен, то можно вернуться к первому этапу и увеличить число пробных точек, чтобы повторить второй этап с таблицами испытаний большего объема.
Анализ таблиц испытаний позволяет обнаружить несущественные критерии, значения которых мало меняются; выявить зависимые или, наоборот, противоречивые критерии; определить влияние параметрических ограничений на интегральный критерий; выделить несущественные по отношению к какому-либо критерию параметры; выделить паретовское множество решений, определить оптимальные параметры. К наиболее важным результатам анализа таблиц испытаний следует отнести получение допустимого множества моделей и определение ресурсных возможностей моделей по всем локальным критериям качества. Такой подход впервые позволяет вводить в рассмотрение столько локальных критериев, сколько необходимо.
Параметрическая оптимизация реализуется в виде поисковой системы, в которой недостаток априорной информации восполняется за счет текущей, получаемой в виде реакций объекта на искусственно вводимые поисковые воздействия. Некоторые поисковые воздействия вычисляются на основе совокупности прогнозируемых величин, т.е. рассматривается функционал на прогнозируемом движении объекта.
Алгоритм параметрической оптимизации имеет вид
где k - шаг управления; D - окрестность виброрежима; sgn - слоговый символ, означает - знаковая функция; p - символ дифференцирования по времени; C - область значений вектора состояния;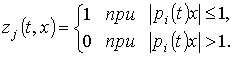 
Его реализация имеет модульную структуру, причем в каждом модуле происходит лишь линейное и релейное преобразование сигналов.
Таким образом, становится реальной возможность обоснования постановки задачи многокритериальной оптимизации - одновременно учитывать множество противоречивых критериев, что привело к созданию качественно нового метода проектирования производственных процессов в растениеводстве.
Библиографическая ссылка
Важенин А.Н., Арютов Б.А. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕХАНИЗИРОВАННЫХ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ ПО УСЛОВИЯМ ИХ ФУНКЦИОНИРОВАНИЯ В РАСТЕНИЕВОДСТВЕ // Современные наукоемкие технологии. – 2010. – № 2. – С. 39-41;URL: https://top-technologies.ru/ru/article/view?id=24441 (дата обращения: 21.11.2024).