Несмотря на то, что решение вопроса о методике расчета величины этого напряжения представляется вполне очевидным, некоторое время назад в ходе обсуждения общей методики проектирования многофазных ЭМС переменного тока вокруг названного вопроса возникла дискуссия.
В связи с этим авторы данной работы сочли необходимым изложить ниже самым подробным образом ход своих рассуждений по рассматриваемому вопросу (даже рискуя местами повторить общеизвестные истины и привести излишне подробные математические выкладки).
Подойдем к рассмотрению затронутой темы последовательно. Начнем с того, как определяется действующее значение переменного напряжения, имеющего синусоидальную форму. Общеизвестно (см., например, [1]), что действующее значение Uд переменного напряжения u любой формы вычисляется в соответствии со следующей формулой (в случае постоянного напряжения действующее значение этого напряжения равно его величине):
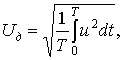 (1)
(1)
где (в случае переменного напряжения, имеющего синусоидальную форму)
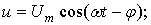 (2)
(2)
Um, ω ,φ - соответственно амплитуда, угловая частота и начальная фаза переменного (синусоидального) напряжения u;
![]() (3)
(3)
T- период; t - время.
В дальнейшем (чтобы максимально упростить изложение вопроса) будем рассматривать случай, когда φ = 0.
На основании (2) определим для этого случая величину u2:
![]() (4)
(4)
Поскольку ![]() (где в рассматриваемом случае
(где в рассматриваемом случае ![]() ), то выражение (4) преобразуется к виду
), то выражение (4) преобразуется к виду
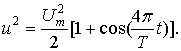 (5)
(5)
Теперь определим значение интеграла 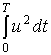 с учетом (5):
с учетом (5):
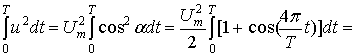
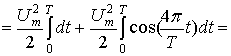
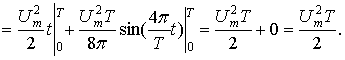 (6)
(6)
После подстановки (6) в (1) получаем:
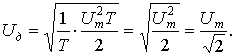 (7)
(7)
Очевидно, что равенство (7) справедливо и при φ ≠ 0
На следующем этапе определим действующее значение периодического несинусоидального напряжения, выражение для которого можно представить в виде следующего гармонического ряда (т.е. ряда Фурье):
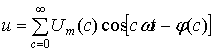 , (8)
, (8)
где ω определяется по формуле (3);
c - номер (порядок) гармоники напряжения u;Um(c) ,φ (c) - соответственно амплитуда и фаза c-ой гармоники напряжения u.
Из выражения (1) следует, что квадрат действующего значения такого напряжения может быть определен по следующей формуле:
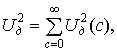 (9)
(9)
где Uд- действующее значение напряжения u;Uд(c) - действующее значение c-ой гармоники напряжения u;
![]() (10)
(10)
С учетом (9) и (10) выражение для величины Uд принимает вид
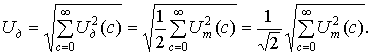 (11)
(11)
Для проверки справедливости выражения (11) рассмотрим случай, когда u = u(t) представляет собой меандр (рис. 1), т.е. когда
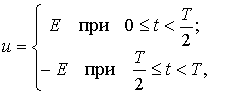 (12)
(12)
где E=const при t=var.
Подставив (12) в (1), получаем следующее:
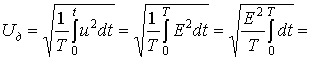 (13)
(13)
С другой стороны, функция (12) может быть представлена в виде гармонического ряда (8), в котором c=2k-1 (где k=1,2,3,... ) и
![]() (14)
(14)
После подстановки (14) в (11) получаем:
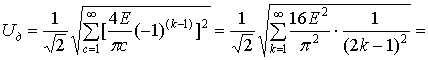
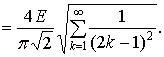 (15)
(15)
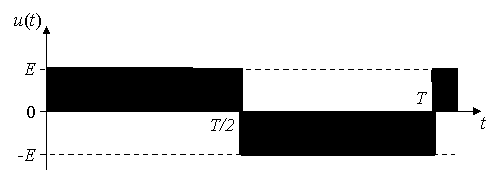
Рис. 1. Форма напряжения u(t)
Известно (см., например, [4]), что сумма сходящегося ряда 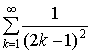 равна следующему:
равна следующему:
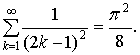 (16)
(16)
После подстановки (16) в (15) окончательно получаем:
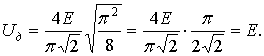 (17)
(17)
Выражения (17) и (13) адекватны. Отсюда можно сделать вывод о том, что выражение (11) справедливо.
После того, как на соответствующем этапе проектирования соответствующей электромеханической системы (например, инверторного электропривода переменного тока - как синхронного, так и асинхронного) было определено действующее значение выходного фазного напряжения преобразователя частоты (оно же - фазное напряжение статора электродвигателя, в случае проектирования электропривода), можем перейти к определению величины напряжения на входе автономного инвертора напряжения (АИН), входящего в состав преобразователя частоты со звеном постоянного тока и являющегося одним из основных элементов системы привода.
Известно (см., например, [2, 3, 5]), что фазное напряжение i-ой фазы ms-фазного АИН (где ![]() ) связано с величиной Uu входного напряжения АИН следующим образом:
) связано с величиной Uu входного напряжения АИН следующим образом:
![]() , (18)
, (18)
где ui - фазное напряжение i-ой фазы АИН; fi - коммутационная функция i-ой фазы АИН (иначе говоря, - коммутационная функция i-ой точки подключения нагрузки к АИН).
Напряжение ui может быть представлено в виде гармонического ряда, аналогичного ряду (8):
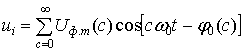 , (19)
, (19)
где ω0- угловая частота основной гармоники выходного (фазного) напряжения АИН; U ф.т. (с) - амплитуда с-ой гармоники напряжения ui, φ0 - фаза (иначе говоря, - начальная фаза) c-ой гармоники напряжения ui.
Коммутационная функция fi также может быть представлена в виде соответствующего ряда Фурье:
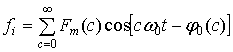 , (20)
, (20)
где Fт(c) - амплитуда c-ой гармоники коммутационной функции fi.
При этом величины U ф.т. (c) и Fт (с) связаны между собой следующим образом:
![]() . (21)
. (21)
С учетом этих обозначений действующее значение выходного (фазного) напряжения АИН на основании (10) и (11) может быть выражено следующим образом:
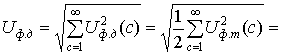
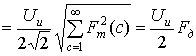 , (22)
, (22)
где Fд- «действующее» (если использовать терминологию, аналогичную той, что применяется для фазного напряжения) значение коммутационной функции fi;
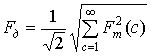 . (23)
. (23)
Из (22) следует, что действующее значение выходного (фазного) напряжения АИН и величина напряжения на входе (т.е. во входной цепи) АИН связаны следующим соотношением:
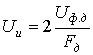 . (24)
. (24)
Одним из наиболее широко распространенных и наиболее просто реализуемых алгоритмов управления вентильными элементами АИН является так называемое 180-градусное управление. При алгоритме управления ключами АИН каждая фазная обмотка статора электродвигателя первую половину периода выходного напряжения инвертора подключена к положительному «полюсу» звена постоянного тока, расположенного на входе АИН, а вторую половину названного периода она подключена к отрицательному «полюсу» этого звена. При этом fi описывается выражением, аналогичным выражению (12),
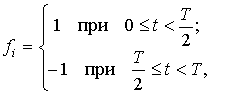 (25)
(25)
а график функции fi=fi(t) имеет вид меандра, аналогичного тому, что показан на рис 1 (см. рис. 2), а Fд =1. Следовательно, при 180-градусном управлении вентилями АИН имеет место соотношение:
![]() . (26)
. (26)
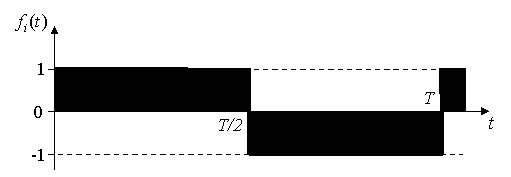
Рис. 2. График коммутационной функции при 180-градусном управлении вентильными элементами АИН
Отсюда, в частности следует, что если U ф.д = 220 В, то при 180-градусном управлении вентильными элементами АИН Uu = 440 В.
Таким образом, в ходе выполнения данной работы была получена формула (24), описывающая соотношение между действующим значением выходного (фазного) напряжения АИН и напряжением на входе этого инвертора. Эта формула, в частности, может быть использована для определения напряжения, которое должно быть обеспечено во входной цепи АИН, при любом алгоритме управления вентильными элементами инвертора.
СПИСОК ЛИТЕРАТУРЫ
- Бессонов Л.А. Теоретические основы электротехники. - М.: Высшая школа, 1967. - 776 с.
- Бражников А.В. Многофазный инверторный электропривод с различным исполнением ротора асинхронного двигателя // Диссертация канд. техн. наук, защищена 26.06.1985 г., № ГР 01830052658. - Красноярск, 1985. - 210 с.
- Бражников А.В. и др. Модель обобщенного электромеханического преобразователя энергии // Сборник научных трудов Всероссийской научной конференции «Молодежь и наука - третье тысячелетие». - Красноярск: Издательство КРО НС «Интеграция», 2007. - С. 405-414.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1984. - 832 с.
- Кочетков В.П., Бражников А.В., Дубровский И.Л. Теория электропривода. - Красноярск: Издательство КрПИ, 1991. - 140 с.
Библиографическая ссылка
Бражников А.В., Бабин В.А., Гилёв А.В., Белозеров И.Р. РАСЧЕТ НАПРЯЖЕНИЯ НА ВХОДЕ МНОГОФАЗНОГО АВТОНОМНОГО ИНВЕРТОРА НАПРЯЖЕНИЯ // Современные наукоемкие технологии. 2010. № 1. С. 9-15;URL: https://top-technologies.ru/ru/article/view?id=24358 (дата обращения: 05.03.2026).



