Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Подопригора В.Г.

Статья в формате PDF

140 KB

Нанообъекты были известны и ранее (например, коллоиды), но в последнее время произошло выделение таких понятий, как наноструктура, нанокластер и связанных с ними явлений в отдельную область исследований. Это произошло, главным образом, в результате значительного прогресса в получении и исследовании нанообъектов, возникновении новых наноматериалов, нанотехнологий и наноустройств [1].

Выделяются две основные характеристические черты нанокластеров, отличающих их как от атомов, так и от массивных твердых тел - это наличие поверхности и квантовые ограничения коллективных процессов, связанных с фононами, электронами, плазмонами, магнонами и т.д. Появление реальной поверхности для кластера не имеет четкой границы, зависит от применяемого метода и соответствует, по-видимому, минимальному размеру кластера около 1 нм. Максимальный размер наночастицы, при котором с помощью современных методов различимо влияние поверхности на их свойства, составляет около 100 нм. Для наблюдения квантовых ограничений минимальный размер не лимитирован, а максимальный - связан с длиной волны носителей и также должен быть менее 100 нм. Эта верхняя граница нанообласти соответствует минимальным элементам в больших интегральных схемах (БИС), широко применяемым в полупроводниковой и компьютерной технике. Интересно, что многие вирусы имеют размер 10 нм. А 1 нм. почти точно соответствует характерному размеру белковых молекул (в частности, радиус двойной спирали молекул ДНК равен именно 1 нм.).

Большой интерес исследователей вызывают молекулярные анизотропные системы (молекулярные кристаллы из больших и малых молекул, их поверхности, тонкие планки нанометровых размеров, адсорбированные монослои, пленки Лэнгмюр - Блоджетт, жидкие кристаллы на поверхности твердого тела и т.д.), в которых молекулы связаны между собой слабыми вандерваальсовыми силами. Характерным является значительный отклик свойств и структуры этих систем на малые внешние воздействия (например, электрического и магнитного полей), что позволяет создавать на их основе разнообразные активные элементы оптоэлектроники, квантовой электроники, лазерной техники, работающих в наноразмерной области.

Простое изменение поля, температуры, замещение одного атома на другой в молекуле вещества - могут в корне изменить свойства структуры (например, превратить изолятор в сверхпроводник), что позволяет осуществлять целенаправленный синтез новых материалов с заранее заданными свойствами.

Целью настоящей работы явилось изучение влияния поверхностных эффектов при определении динамических и электрооптических свойств нанокластеров и молекулярных систем, которые, по меньшей мере, в одном направлении имеют нанометровые размеры.

Молекулярная динамика, электрооптика и колебательная спектроскопия являются эффективными методами изучения физических свойств нанокластеров, монослоев и тонких пленок. Для извлечения достоверной информации из спектров неупругого рассеяния нейтронов, оптических и микроволновых спектров необходимо корректно решить полную динамическую задачу для этих систем.

Для этого необходимо вычислить силовые постоянные, пропорциональные вторым производным от потенциальной энергии U кристалла по трансляционным и ориентационным смещениям молекул в положении равновесия. Решение задачи существенно упрощается при наличии аналитического выражения для U. В работе использована модель атом - атомных потенциалов, предложенная А.Н. Китайгородским, дополненная введением в потенциал членов, отвечающих за мультипольное и трехчастичное взаимодействие частиц. [2]

Динамика сверхтонкой пленки рассчитывалась в модели пластины, в которой элементарная ячейка имеет 6lN степеней свободы, где l - число слоев, N - число неэквивалентных молекул в каждом слое. Далее, диагонализируя полную динамическую матрицу силовых постоянных, находятся все собственные частоты и собственные векторы колебаний системы.

В качестве объектов были выбраны "чистые" поверхности молекулярных кристаллов антрацена и β-парадихлорбензола, адсорбированные слои этана на графите (в 2-х модификациях), а также система "жидкий кристалл 7 цианобифинила - кристаллическая подложка (кварц, триглициносульфат).

В таблице 1 приведены значения частот решеточных колебаний объемной структуры и поверхности кристалла β-парадихлорбензола (1 молекула в элементарной ячейке)

Таблица 1

Видно, что частоты поверхностных колебаний уменьшаются по сравнению с объемом от 5 до 50%. Формы собственных колебаний становятся смешанными, а не чисто ориентационными, как в объемном кристалле. Решена динамическая задача и для этана, адсорбированного на графите. Для этой системы экспериментально установлена структура и энергетический спектр фононов. Были рассчитаны дисперсионные зависимости частот, плотность фотонных состояний, сечения неупругого рассеяния нейтронов, удовлетворительно совпадающие с экспериментом. Зная дисперсионные зависимости частот в различных направлениях зоны Бриллюэна и плотность состояний фононов, получены все компоненты тензора A амплитуд молекул этана на графите (фаза S₃):

(Квадраты трансляционных смещений имеют размерность , либрационных - рад ², смешанных -  рад).

Диагонализовав тензор A, получим средние квадраты трансляционных и ориентационных смещений молекул около осей инерции. Они равны: 0,091, 0,170, 0,008  и 0,011, 0,049, 0,008 рад ², что соответствует средним трансляционным амплитудам 0,22  и средним углам качания молекул на поверхности 8°. Это в несколько раз больше значений амплитуд, найденных для молекул в кристаллическом объеме.

В молекулярных упорядоченных средах макроскопическую восприимчивость, характеризующую взаимодействие света с веществом, можно найти, исходя лишь из структуры и электронных характеристик молекул. Так, линейная диэлектрическая восприимчивость, определяющая всю линейную кристаллооптику, определяется, как [2]

,                                                    (2)

где эффективная поляризуемость m-й молекулы, V- объем элементарной ячейки, w -частота возбуждающего света, тензор коэффициентов локального поля, связывающий компоненты макроскопического поля и поля, действующего на m-ю молекулу элементарной ячейки. Для решетки, образованной Z молекулами, тензор локального поля имеет вид:

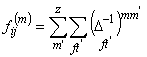
где блочная матрица размерности 3Zx3Z, под матрицы которой определяются уравнением:

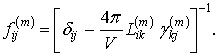                                                    (3)

В формуле (3) δ_ij - символ Кронекера, L^(m) - анизотропный структурный фактор (Лорентца), описывающий распределение диполей в плоскости кристаллической решетки. Компоненты данного тензора рассчитываются модифицированным методом Эвальда для плоских структур [2] по атомным подрешеткам с последующим усреднением на молекулу.

Эффективная поляризуемость молекулы в кристаллической среде определяется путем прибавления к поляризуемости α свободной молекулы добавок, возникающих из-за межмолекулярных дисперсионных взаимодействий [2]:

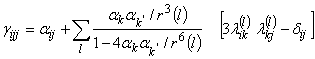                                    (4)

Здесь α_k и α^_ki- поляризуемости отдельных атомов, принадлежащих разным молекулам и образующих связь с номером l, r(l) - расстояние между ними, элементы матрицы направляющих косинусов l-й связи, переводящей компоненты поляризуемости в прямоугольную систему координат. Ряд (4) сходится, если число суммируемых атомов достигает 25-30 тысяч. (При изменении радиуса суммирования с 4 до 4,5 нм. значения компонент тензора добавок ( 2-й член в 3) изменяются не более чем на 2 %). Если молекула имеет постоянный дипольный момент, то в эффективную поляризуемость добавляется член, пропорциональный нелинейной поляризуемости.

Для примера в таблице 2 приведены поляризуемость α для свободной молекулы и эффективная поляризуемость γ для молекулы этана, адсорбированного на графите (S₃ фаза).

Таблица 2

Изучение процессов формирования на кристаллических поверхностях атомов или молекул другого вещества позволит вплотную приблизиться к проблеме конструирования так называемых "квантовых точек", которые могут удерживать 1 или несколько электронов. Это уже сейчас позволило создавать одноэлектронные транзисторы, запоминающие устройства с крайне малым энергопотреблением и размером около 100 нм., причем сама "ловушка" электронов имеет диаметр около 10 нм. [3].

Исследование характерных особенностей веществ на расстояниях порядка нанометров создает новые возможности для создания технологических приемов, связанных с физикой, химией, электроникой, материаловедением и многими другими областями науки. Развитие новых методик и получение новых материалов приведет к революционным изменениям в информационных технологиях, производстве конструкционных материалов, конструировании сверхточных устройств, изготовлении фармацевтических препаратов.

СПИСОК ЛИТЕРАТУРЫ:

1. Белая книга по нанотехнологиям. - М., И. ЛКИ, - 2007.
2. Ботович А.Н., Подопригора В.Г., Шабанев В.Ф. Комбинационное рассеяние света в молекулярных кристаллах. Новосибирск. Наука. - 1999.
3. Кобаяси Н. Введение в нанотехнологию. - М., Бином. - 2008.

Библиографическая ссылка