Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

M. M

В настоящее время имеются методы обработки и проведение анализа результатов многофакторного эксперимента. Однако увидеть одновременно влияние сочетания всех участвующих в эксперименте независимых переменных факторов на параметр оптимизации, когда он находится в заданной области значений, не представляется возможным. Нами предлагается номограммный метод анализа результатов многофакторного эксперимента, представленного в виде уравнения регрессии, адекватно описывающего функцию отклика. С помощью номограммы определяются допустимые пределы колебаний всех независимых переменных факторов участвующих в эксперименте, обеспечивающих нахождение параметра оптимизации не только в экстремальной точке, но и в области заданных значений.

Статья в формате PDF

1004 KB

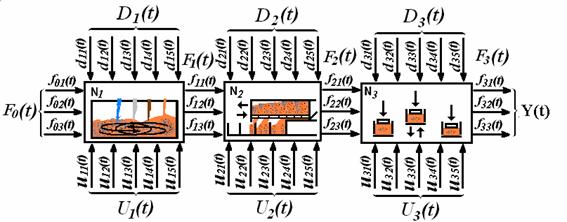
Рис. 1. Блок-схема последовательных состояний БТС - модели технологического процесса изготовления кормовых брикетов из кормовых смесей. D_i - независимы переменные факторы; F_i - внешние факторы воздействующие на процесс; U_i - факторы управления системой; Y_i - последовательное состояние параметра оптимизации биотехногенной системы ; N_i - последовательное состояние биотехногенной системы.

Например, технологический процесс изготовления кормовых брикетов включает смешивание компонентов кормовой смеси (N₁), заполнение матрицы кормовой смесью (N₂) и прессование кормовых брикетов (N₃), рис. 1. Наиболее значимыми независимыми и управляемыми факторами экспериментатор выбрал x₁ - массу инерционной решетки в загрузочном ящике, x₂ - время виброуплотнения кормовой смеси в матрице, x₃ - скорость загрузочного ящика. Функция отклика системы Y(t) в данном случае определяет коэффициент вариации массы кормового брикета.

В общем виде математическая модель функционирования БТС представляет собой полином, который разлагается по методу Бокса-Уильсона в степенной ряд вида:

Y=b₀ + b₁x₁ + b₂x₂ +...+ b_nx_n + b_1,1 x²₁+ b_2,2 x²₂+...+ b_n,n x²_n+b _1,2x _1x2+

 b_1,3x₁x₃ +b_1nx₁x_n+b_2,3x₂x₃+...+b_2,nx₂x_n+b_(n-1),nx_n-1x_n+...     (1)

где: Y - параметр оптимизации состояния биотехногенной системы;b₀,b₁...b_(n-1)n  - коэффициенты регрессии;x₁,x₂,...,x_n  - независимые переменные факторы, определяющие условия функционирования биотехногенной системы, такие как внешние и внутренние воздействия на систему, а также факторы управления системой.

Уравнение (1) называют уравнением регрессии, оно адекватно функции отклика биотехногенной системы Y = f (x₁,x₂,..,x_n) и описывает многовекторную область значений параметра оптимизации системы. Исследуют эту область методом трехмерных ее сечений. Эти сечения представляют собой поверхности, уравнения которых получают из уравнения регрессии (1) путем последовательной фиксации на нулевом кодированном уровне всех факторов, кроме двух исследуемых. [2,3]

Коэффициенты регрессии в уравнении (1) определяют методом вариационно-статистической обработки результатов многофакторного эксперимента. Планирование многофакторного эксперимента предусматривает кодирования и варьирования независимых переменных факторов на трех основных уровнях: -1; 0; +1, а также, при необходимости, на верхнем и нижнем звездных уровнях ± 1,215

Например, для проведения многофакторного эксперимента по оптимизации конструктивных и технологических режимов работы вибропресса ПТ-11 при изготовлении кормовых брикетов кодирование интервалы варьирования независимых переменных факторов имеет ниже приведенный вид, таблица 1.

Таблица 1. Кодирование интервалы варьирования независимых переменных факторов

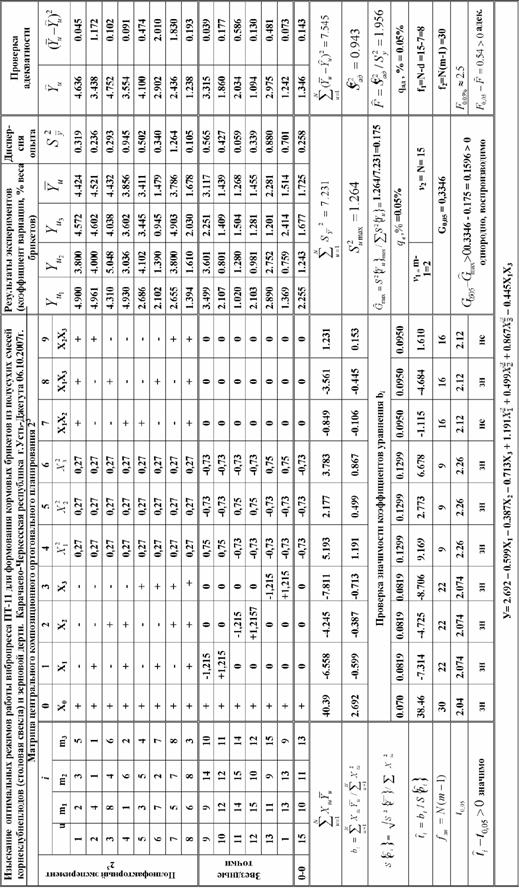
Для проведения многофакторного эксперимента выбирается соответствующая матрица, разрабатывается алгоритм проведения эксперимента. Для центрального композиционного ортогонального плана типа 2³ алгоритм имеет вид, таблица 2. В таблице 2 отображены результаты вариационно-статистической обработки экспериментальных данных, а также уравнение регрессии.

Когда разрабатывались методы исследования уравнения регрессии, еще не было современной вычислительной оргтехники, выполняющей многочисленные операций за короткий промежуток времени. Поэтому в старых методиках предусматриваются оценки коэффициентов регрессии по уровню их значимости (критерий Стьюдента), что находится в рамках 95% доверительного интервала и позволяет исключать из выведенного уравнения регрессии члены с малозначимыми (до 5%) коэффициентами регрессии. Такие упрощения приводят к исключению из анализа некоторых независимых переменных факторов или их сочетания, что упрощает и ускоряет расчеты, но при этом не учитываются их влияния на параметр оптимизации (как пример смотри таблицу №2 сочетания х₁х₂; и х₂х₃). В итоге исследователи получают результаты и делают выводы с неизвестной ошибкой в приделах ±2,5% при нахождении экстремальной точки оптимизируемого параметра.

При нынешней оргтехнике и ее программном обеспечении появилась возможность оставлять в полученном уравнении регрессии все его члены, несмотря на значимость их коэффициентов, это повышает точность полученных результатов, а на продолжительность времени проведения статистических расчетов результатов многофакторного эксперимента, который заметного влияния не оказывает.

Уравнение регрессии в таблице 2 составлено с учетом значимости коэффициентов регрессии по критерию Стьюдента, и имеет вид (2):

У= 2.692 - 0.599Х₁ - 0.387Х₂ - 0.713Х₃ + 1.191X²₁  + 0.499X²₂  + 0.867X²₃  - 0.445Х₁Х₃ (2)

Уравнение регрессии этого же многофакторного эксперимента по формованию кормовых брикетов на вибропрессе ПТ-11 но без учета значимости коэффициента регрессии по критерию Стьюдента имеет вид (3).

(3)

Известны два метода анализа уравнения регрессии, адекватно описывающего функцию отклика (БТС) - аналитический и графический.

Аналитический метод анализа приемлем для функций отклика, частные производные которых по любому фактору можно приравнять к нулю, то есть они неразрывны, монотонны и имеют экстремальные точки. Преимущество аналитического метода анализа перед графическим методом состоит в том, что он позволяет учитывать члены уравнения регрессии с тремя, четырьмя и более сочетаниями факторов. Если исследователь уверен, что все частные производные функции отклика отвечают этим требованиям, то составляется система уравнений из частных производных уравнения регрессии по каждому независимому фактору. Решение системы уравнений, иногда очень громоздкое, позволяет найти значения переменных факторов, при которых параметр оптимизации имеет экстремальное значение.

Определение допускаемых пределов колебаний факторов, при которых параметр оптимизации находится в области заданных значений, практический не решается аналитическим методом.

Таблица 2. Результаты многофакторных экспериментов и их обработка при изыскании оптимальных режимов работы вибропресса ПТ-11 при формовании кормовых брикетов из полусухих смесей корнеплодов (столовая свекла) и зерновой дерти

Графический метод анализа уравнения регрессии - универсальный, к тому же для него разработаны специальные компьютерные программы, к примеру, программа «Matlab-6.0», функционирующая в средах Word 97/2000/2007. Программа позволяет визуализировать уравнение регрессии, в котором переменными остаются только два из всех факторов и их сочетаний, остальные факторы уравнения фиксируются на нулевом, кодированном уровне. Очевидно, при этом методе исследований, члены уравнения регрессии с тремя и более сочетаниями факторов приравниваются к нулю. Поэтому, ориентируясь на графический метод анализа уравнения регрессии, можно заранее составлять его без членов уравнения, содержащих сочетания факторов более двух. Исключение из уравнения регрессии членов с сочетаниями факторов более двух, естественно, приведет к снижению точности полученных результатов.

Одним из достоинств, программы «Matlab-6.0»является то, что она визуализирует уравнение регрессии, представляет поверхность отклика в аксонометрии, а также в проекциях на координатные плоскости. Кроме того, она позволяет, строит проекцию контурных линий поверхности отклика в координатах факторов x_ix_j, обозначающих парные сочетания независимых переменных факторов в уравнении регрессии (рис. 2; 3; 4).

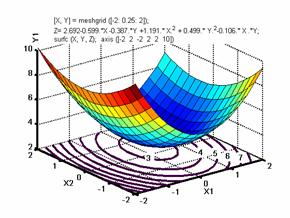
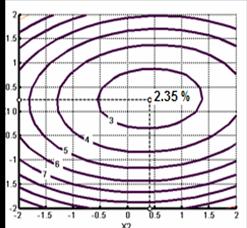
Рис. 2. Поверхность отклика значений коэффициентов вариации масс кормовых брикетов Y₁ в зависимости от массы инерционной сводоразрушающей решетки в мерном ящике (Х₁) и времени вибрации при заполнении ячеек матрицы смесью (Х₂); контурные линии вариации массы кормовых брикетов от взаимодействующих факторов (Х₁) и (Х₂).

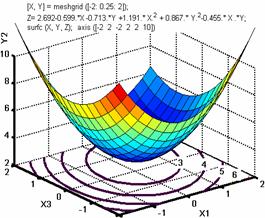
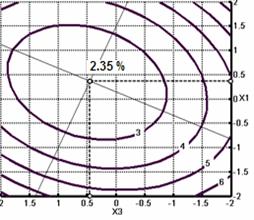
Рис. 3. Поверхность отклика значений коэффициентов вариации масс кормовых брикетов Y₁ в зависимости от массы инерционной сводоразрушающей решетки в мерном ящике (Х₁) и поступательной скорости мерного ящика (Х₃); контурные линии вариации массы кормовых брикетов от взаимодействующих факторов (Х₁) и (Х₃).

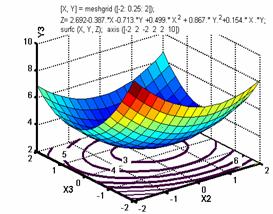
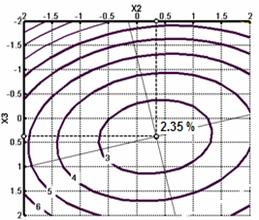
Рис. 4. Поверхность отклика значений коэффициентов вариации масс кормовых брикетов Y₁ в зависимости от времени вибрации при заполнении ячеек матрицы смесью (Х₂); и поступательной скорости мерного ящика (Х₃); контурные линии вариации массы кормовых брикетов от взаимодействующих факторов (Х₂) и (Х₃).

Однако увидеть одновременно влияние сочетания всех участвующих в эксперименте независимых переменных факторов на параметр оптимизации, когда он находится в заданной области значений, не представляется возможным. Уравнение регрессии многофакторного эксперимента вида 2³ содержит только три парных сочетания независимых переменных факторов - х₁х₂; х₁х₃; х₂х₃, (рис 2; 3; 4); вида 2⁴ содержит шесть таких парных сочетаний независимых переменных факторов - х₁х₂; х₁х₃; х₁х₄; х₂х₃; х₂х₄; х₃х₄,; вида 2⁵ содержит 10 парных сочетаний независимых переменных факторов - х₁х₂; х₁х₃; х₁х₄; х₁х₅; х₂х₃; х₂х₄; х₂х₅; х₃х₄; х₃х₅; х₄х₅. В уравнении регрессии на параметр оптимизации Y влияют как отдельные сочетания взаимодействующих факторов, так и вся их совокупность. В настоящее время задачу определения значений пределов колебаний независимых переменных факторов, обеспечивающих нахождения параметра оптимизации в заданной области, его значений, решают без учета совокупного влияния парных сочетаний факторов. Это затрудняет применение на практике полученных результатов и их корректировку для заданного уровня оптимизируемого параметра, а также отсутствует методика визуализации и проведения анализа одновременно взаимодействующих переменных факторов.

Нами предлагается номограммный метод анализа результатов многофакторного эксперимента, представленного в виде уравнения регрессии, адекватно описывающего функцию отклика БТС. С помощью номограммы определяются допустимые пределы колебаний всех независимых переменных факторов участвующих в эксперименте, обеспечивающих нахождение параметра оптимизации не только в экстремальной точке, но и в области заданных значений.

Номограммный метод анализа уравнения регрессии учитывает результаты парных взаимодействий факторов на допускаемые пределы колебаний этих факторов, при которых параметр оптимизации не выходит за пределы области заданных значений.

Этот метод анализа дает возможность увидеть одновременно влияние на параметр оптимизации всех участвующих в уравнении регрессии независимых переменных факторов- х₁; х₂; х₃ то есть, как они действуют на реальный технологический процесс.

Становится возможным определение влияния изменения предела колебания каждого из переменных факторов на величину параметра оптимизации.

Использование номограммного метода анализа дает возможность осознанно изменять пределы отклонения каждого из исследуемых факторов в многофакторном эксперименте с учетом возможностей биотехногенной системы для получения заданной области значений параметра оптимизации.

Предложенный номограммный метод анализа результатов многофакторного эксперимента повышает точность нахождения параметра оптимизации.

Разработаны схемы построения номограмм для анализа результатов многофакторных экспериментов с различным числом независимых переменных факторов, рис.5.

В этих схемах главные ординаты и абсциссы выделены жирными линиями и на них отложены раскодированные значения переменных факторов в натуральных единицах измерений. Квадратами в этих координатах обозначены графические изображения решений уравнения регрессии, которые представляют собой проекции контурных линий поверхности отклика на горизонтальную плоскость и в зависимости от сочетания двух переменных факторов, действующих в многофакторном эксперименте, они отложены на своих координатных осях в кодированном масштабе. Метками в виде кружочков на координатных осях отмечены место нахождения пределов колебаний переменных факторов, при которых обеспечивается область заданного значения параметра оптимизации. Тонкими пунктирными линиями обозначены направления проецирования на координатные оси области заданного значения параметра оптимизации, изображенных на частных визуализированных уравнениях регрессии.

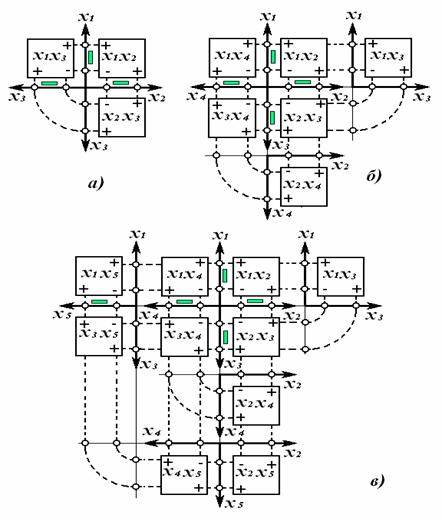
Рис. 5. Схемы построения номограмм для анализа результатов многофакторных экспериментов с алгоритмами планирования а) ПФЭ типа 2³; б) ПФЭ типа 2⁴; в) ПФЭ типа 2⁵.

Пример номограммного метода анализа результатов многофакторного эксперимента 2³ показан на рис.6. Уравнение регрессии (3), является результатом вариационно-статистической обработки данных многофакторного эксперимента типа 2³ и адекватно описывает функцию отклика БТС. Многофакторный эксперимент проведен автором с целью отыскания оптимальных технологических режимов работы вибропресса ПТ-11 производства ОАО «Завод «Красная Пресня» для формования кормовых брикетов из смесей корнеплодов и зерновой дерти.[1] Алгоритм проведения опытов и расчеты представлены в
таблице 2.

Для построения номограммы необходимо, чтобы визуализация частных уравнений регрессии программой «Matlab-6» выполнялась в одном масштабе, то есть содержание команды axis должно быть общим и постоянным для всех решений в графическом виде. Монтаж номограммы необходимо вести с соблюдением кодовых направлений (+), и (-), а также сопряжением кодированных факторных осей по вертикали и горизонтали. Соответствующее положение визуализации обеспечивается программой «Matlab-6».

За допускаемый предел колебаний какого-либо из исследуемых факторов следует принимать минимальную проекцию из всех проекций заданной области значений параметра оптимизации на ось этого же фактора. На главных координатных осях стрелками указаны проекции - пределы колебаний факторов, обеспечивающих нахождение в заданной области значений параметра оптимизации.

Анализируемое уравнение регрессии является результатом вариационно-статистической обработки многофакторного эксперимента типа 2³ поэтому номограмму для анализа результатов эксперимента будем строить по схеме а), рис. 5.

Воспользовавшись компьютерной программой «Matlab-6.0» и программой «Paint», построим номограмму, (рис. 6), для анализа и исследования уравнения регрессии (3).

В качестве примера поставим задачу, определить при каких допускаемых пределах колебаний переменных факторов Х₁, Х₂, Х₃ многофакторного эксперимента параметр оптимизации (коэффициент вариации массы кормовых брикетов прессуемых на вибропрессе ПТ-11) не превышает 3%.

Из рисунка 6 выбираем область значений параметра, оптимизации, ограниченной контурной линией с цифрой 3%, и имеющей наименьшую длину проекции на координатные оси. Наименьшими проекции на координатные оси оказались проекции контурной линии 3%, в квадранте Х₁Х₂ (правый верхний квадрант). Принимаем этот квадрант за начало отсчета и проецируем ее контуры на соответствующие контурные линии с цифрой 3 в квадрантах Х₁Х₃ и Х₂Х₃. Проецирующие линии отсекают на координатных осях отрезки (отмеченные стрелками с обеих сторон), соответствующие допускаемым пределам колебаний факторов, при которых коэффициент вариации массы кормовых брикетов не превышает заданные 3 %.

Например:

Коэффициент вариации не более 3 % обеспечивается при значениях факторов: Х₁ - масса инерционной решетки находиться в пределе М = 8...14 кг; Х₂ - время вибрации при заполнении матрицы t =0,86...1,26 с; Х₃ - скорость движения мерного ящика v =1,45..2,12 м/с. В нашем примере возможная ошибка:

по фактору Х₁ = ;

по фактору Х₂ =

по фактору Х₃ =

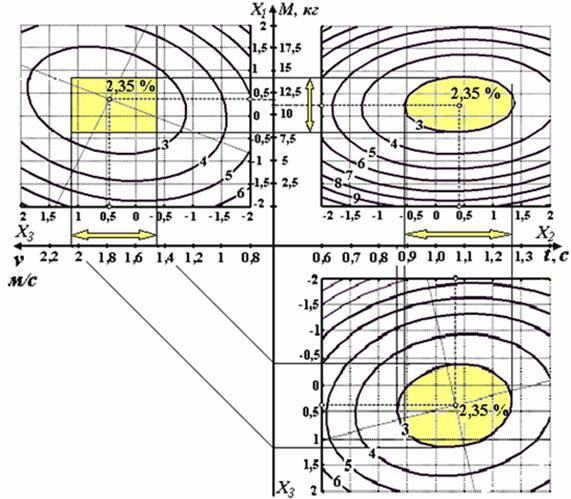
Рис. 6. Номограмма для анализа и определения допускаемых пределов колебаний факторов Х₁, Х₂, Х₃, обеспечивающих нахождение коэффициента вариации массы кормовых брикетов в заданной области - не более 3%

Из проведанного анализа результатов многофакторного эксперимента видно, что нам удалось избежать ошибки при определении допускаемых колебаний фактора Х₁ на 47,8%, а фактора Х₃ - на 35,5%.

Чем значимее коэффициент при исследуемом факторе уравнения регрессии, тем больше может быть ошибка пределов колебаний этого фактора, обеспечивающего нахождение параметра оптимизации в заданной области значения.

Повторно проведенные контрольные опыты на производственной базе ООО «Агрофирмы «Джаше» с целью проверки результатов полученных с использованием номограммного метода анализа результатов МФЭ подтвердили сходимость результатов с достоверностью 95%.

Коэффициент вариации массы формованных кормовых брикетов на вибропрессе ПТ-11 на режиме с показателями факторов Х₁ = 11±3кг; Х₂= 1,1±0,2с; Х₃= 1,79±0,34м/с; не превышает 3%.

Выводы

Номограммный метод анализа предназначен для визуального исследования результатов многофакторного эксперимента, для определения допускаемых пределов колебаний независимых переменных факторов, обеспечивающих нахождение параметра оптимизации БТС в заданной области значений.

СПИСОК ЛИТЕРАТУРЫ:

1. Джашеев К.А.-М Корм брикетируется на строительном оборудовании // Сельский механизатор, 2008, № 2.
2. Джашеева З.А.-М «Мука растительная из плодов расторопши пятнистой» как антиоксидант в молочном жире.
   // Современные наукоемкие технологии 2008, №3.
3. Митков А.Л., Кардашевский С.В. Статистические методы в сельхозмашиностроении. // М., Изд. «Машиностроение» 1978.-360с.

Библиографическая ссылка