Пассивные интегральные компоненты (пленочные резисторы, аттенюаторы, поглощающие нагрузки, конденсаторы, индуктивности, фильтры и пр.) предназначены для монтажа в полосковые конструкции, поэтому их параметры и частотные характеристики на СВЧ определяют в полосковых направляющих структурах с заданной геометрией поперечного сечения и известных параметрах подложки. Разнообразие вариантов установки в полосковые конструкции (поверхностный монтаж перевернутым кристаллом, в разрыв полосковой линии или в зазор между платами и др.) требует построения универсальных моделей RLC компонентов, позволяющих прогнозировать частотные характеристики с учетом способов монтажа. Несмотря на широкое развитие средств автоматизированного проектирования в библиотеках моделей электронных компонентов, в том числе и зарубежных, отсутствует информация о навесных RLC структурах. Отсутствует и метрологическая нормативная база для измерений параметров электронных компонентов в полосковых направляющих системах. Цель настоящей публикации состоит в привлечении внимания широкого круга специалистов: метрологов, разработчиков ВЧ и СВЧ аппаратуры к решению обсуждаемой проблемы.
Конструкции, модели, параметры
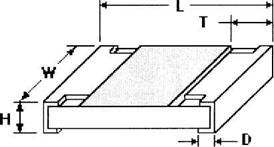
Навесные пассивные электронные компоненты конструктивно выполняются в виде чипов на изоляционной подложке (поликор, нитрид алюминия и пр.) с торцевыми охватывающими контактами для поверхностного монтажа. Резистивные, изоляционные и проводниковые пленки прямоугольной или более сложной формы формируют на поверхности подложки методами тонкопленочной технологии. Габаритные размеры компонентов соответствует стандартным международным типоразмерам 0805 (3,2x1,6 мм), 1206 (2х1,25 мм), 0603 (1,6x0,8 мм) и 0402 (1x0,5 мм). Торцевые контакты располагают на противоположных сторонах, а поверхностные - на трех, либо четырех сторонах подложки (рис.1). Резистивные компоненты, выполняющие функции мощных поглощающих нагрузок, устанавливают на металлических основаниях. Одна контактная площадка имеет ленточный вывод для подключения к полосковой линии, а вторая - соединяется с нижним слоем металлизации торцевым контактом.
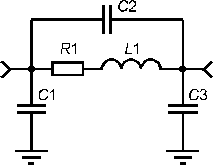
Схемная модель чип-резистора, состоящая из резистора, индуктивности и трех емкостей приведена на рис. 2. Численные значения индуктивности и емкостей сложным образом связаны с геометрией резистивного слоя, контактных площадок, толщиной и диэлектрическими проницаемостями пластин, на которых сформированы резистор и полосковая
линия.
Схемные модели чип-резисторов и индуктивностей с топологией типа меандр могут содержать помимо сосредоточенных элементов отрезки длинных линий. Следует подчеркнуть, что наиболее сложной для моделирования является область монтажа компонента в полосковую линию передачи. Поэтому задачу восстановления параметров схемных моделей необходимо решать с помощью процедуры измерений.
|
|
|
|
Рис. 1. Конструкция чип-резистора для планарного монтажа |
Рис. 2. Cхемная модель чип-резистора
|
Аппаратура, измерения и обработка данных
Электромагнитные характеристики навесных пассивных электронных компонентов определяют по результатам измерений векторными анализаторами цепей волновых параметров рассеяния [S-параметров] контактных устройств с коаксиальными соединителями [1]. Контактные устройства (рис. 3) состоят из коаксиально-полосковых переходов и полосковых линий. Измеряемые компоненты устанавливают между торцами двух полосковых линий, в разрыве полоскового проводника, либо на торце одной полосковой линии при измерении параметров резистивных поглощающих нагрузок. Для восстановления S-параметров компонента относительно его физических границ используют различные приемы исключения влияния окружающих цепей (коаксиально-полосковых переходов, полосковых линий и др.), основанные на преобразованиях Фурье и фильтрации типа «временное» или «спектральное окно», либо матричных способах вынесения [2-4].

Рис. 3. Контактное устройство
Однако, в отличие от измерений в 50-омном стандартном коаксиальном канале, S-параметры компонента восстанавливают относительно волнового сопротивления Zв полосковой линии передачи, в которую он был установлен. Это волновое сопротивление имеет частотно-зависимую величину и зачастую неизвестно, что создает значительные трудности для восстановления численных значений параметров схемных моделей и при монтаже компонентов в полосковые конструкции с другой геометрией поперечного сечения и с другим материалом подложки.
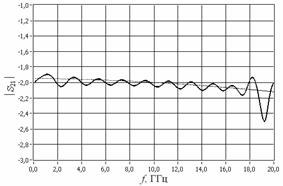
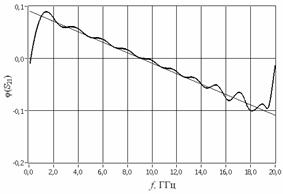
При фильтрации данных измерений методом «спектрального окна» электронные компоненты устанавливают в разрыве достаточно длинной полосковой линии и измеряют коэффициент отражения или передачи контактного устройства в широкой полосе частот. Исходный массив результатов измерений подвергают прямому комплексному преобразованию Фурье. В амплитудном спектре данных (рис. 4) с помощью фильтра типа «спектральное окно» выделяют участок, несущий информацию о комплексном коэффициенте отражения S11 или передачи S12 компонента, аналогичные операции выполняют с данными измерений контактного устройства с полосковой линией и короткозамыкателем в качестве эталона отражения вместо измеряемого объекта. После деления выделенных спектров друг на друга и обратного преобразования Фурье полученного результата восстанавливают искомую частотную зависимость параметра рассеяния относительно физических границ электронного компонента. Недостаток такой процедуры обработки данных состоит в появлении волнообразной погрешности, обусловленной эффектом Гиббса (рис. 5а, б).
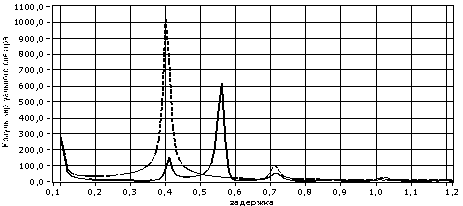
Рис. 4. Амплитудный спектр коэффициента отражения контактного устройства
|
a) |
б) |
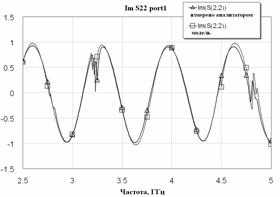
Рис. 5. Восстановленные а) модуль и б) фаза коэффициента передачи аттенюатора (волнообразные функции)
Обработка результатов измерений с помощью процедуры матричного вынесения предполагает определений параметров виртуальных цепей погрешности, окружающих измеряемый электронный компонент. Для определения волновых матриц рассеяния или передачи виртуальных цепей и эффективной диэлектрической проницаемости полосковой линии к коаксиально-полосковым переходам подключают отражающие отрезки полосковых линий разной длины и проходную линию.
По результатам измерений контактного устройства с полосковыми линиями определяют искомые параметры волновых матриц виртуальных цепей погрешности на всех частотах. Используют матричную процедуру исключения окружающих цепей из результатов измерения контактного устройства с электронным компонентом. Недостаток матричного восстановления волновых параметров рассеяния электронных компонентов состоит в том, что эффективное устранение окружающих цепей возможно не во всем непрерывном диапазоне частот, а в отдельных частотных окнах. Границы частотных окон определяются длинами отрезков полосковых линий (рис. 6).
Численные значения параметров схемных моделей электронных компонентов могут быть получены методами параметрической оптимизации целевой функции, построенной на основе S-параметров, восстановленных фильтрацией окнами или матричным вынесением окружающих цепей. Достоверность и точность результатов будет зависеть от того, как и с какой точностью восстановлена зависимость волнового сопротивления полосковой линии от частоты электромагнитных колебаний. Альтернативным способом решения задачи, свободным от этого недостатка, является идентификация параметров моделей компонентов вместе с параметрами модели контактного устройства, в котором они измерялись. Идентификация параметров модели может быть проведена и путем фильтрации пространственных гармоник, возникающих при использовании достаточно протяженных полосковых линий передачи, в которые устанавливаются электронные компоненты. Такое решение не требует восстановления полной модели контактного устройства, а также параметров полосковой линии передачи, в том числе и ее волнового сопротивления.
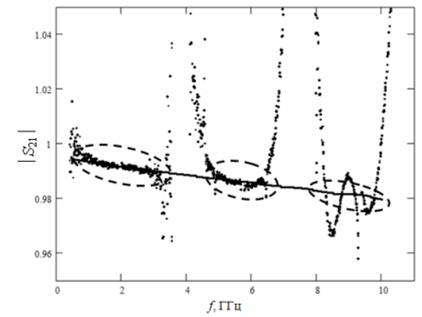
Рис. 6. Частотная зависимость модуля коэффициента передачи полосковой линии (изображена точками)
Массивы измеренных данных содержат скрытую информацию об электромагнитных характеристиках компонента, коаксиально-полосковых переходов, волновом сопротивлении полосковой линии передачи, величине ее эффективной диэлектрической проницаемости, коэффициенте затухания волны, обусловленном как потерями в проводнике и подложке, так и излучением в окружающую среду. Все эти величины являются либо числами, либо относительно медленными гладкими функциями частоты по сравнению с результатами измерений S-параметров контактного устройства, что обусловлено использованием достаточно длинных полосковых линий.
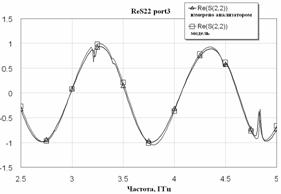
Поэтому оптимально подобранная математическая модель коаксиально-полосковых переходов, эффективные модели полосковых, в том числе и связанных линий, из библиотек САПР позволяют с весьма высокой точностью воспроизвести методами идентификации результаты измерений контактного устройства в достаточно широких окнах частотного диапазона. Результаты измерений векторным анализатором цепей реальной и мнимой частей коэффициента отражения на входе контактного устройства в частотном окне 0,4 ÷ 5ГГц и результаты моделирования этих измерений показаны на рис. 7а, б.
Высокая эффективность (точность) полученного результата обусловлена тем, что в процедуре оптимизации используются весьма большие массивы данных, а количество параметров, описывающих модели коаксиально-полосковых переходов и связанных полосковых линий, на несколько порядков меньше.
|
а) |
б) |
Рис. 7. Результаты измерений и их моделирование в частотном окне
а) Мнимая часть коэффициента отражения
б) Реальная часть коэффициента отражения
Заключение
Основное преимущество идентификации по сравнению с методами матричного вынесения и фильтрации окнами состоит в возможности восстановления абсолютных (параметров схемных моделей), а не относительных (S-параметров) величин. Кроме того, наблюдается существенное снижение влияния случайных погрешностей на результаты восстановления относительно малого числа искомых параметров на массивах данных большой
размерности.
СПИСОК ЛИТЕРАТУРЫ:
- Кудрявцев А.М., Никулин С.М. Интеллектуальные информационно-измерительные системы ВЧ и СВЧ диапазона// Н.Новгород: Нижегород. гос. техн. ун-т.- 2006.- с.198.
- Ульриксон Б. Преобразование данных из частотной области во временную// ТИИЭР.- 1986.- Т.74.- №1.-С.84-87.
- Беднов А.В., Кудрявцев А.М., Никулин С.М. Цифровая обработка результатов СВЧ измерений методом «спектрального окна// Датчики и системы. -2004. -№ 6.-С.30-39.
- Вайткус Р.Л. Широкополосный метод вынесения с использованием короткозамкнутой цепи, разомкнутой цепи и промежуточной линии // ТИИЭР, - 1986,- т.74,- №1,- С.81-84.
Библиографическая ссылка
Малышев И.Н., Санкин Ю.И., Кулага И.Г., Никулин С.М. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ПАССИВНЫХ ИНТЕГРАЛЬНЫХ КОМПОНЕНТОВ НА СВЧ // Современные наукоемкие технологии. 2008. № 8. С. 14-18;URL: https://top-technologies.ru/ru/article/view?id=24120 (дата обращения: 12.03.2026).