Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Калмыков И.А. Руденко А.С.

Статья в формате PDF

151 KB

Решение проблемы исследований:

В последние годы в вычислительной технике, в частности цифровой обработке сигналов (ЦОС), появилась практическая потребность в аппаратной реализации алгоритмов, обладающих повышенной вычислительной сложностью. Для обеспечения обработки сигналов в реальном масштабе времени в работе [1] предложено использовать полиномиальную систему класса вычетов (ПСКВ). В то же время высокие требования предъявляются к надежности работы спецпроцессоров (СП) ЦОС. Из существующих подходов к решению задачи построения отказоустойчивых вычислительных структур все большее применение находят методы теории кодирования.

Целенаправленное введение избыточности позволяет обнаружить и исправить ошибки, возникающие в результате отказов элементов вычислительных трактов СП ПСКВ. Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из п оснований ПСКВ (kполн(z) расширенного поля Галуа GF(p^v) на два непересекающихся подмножества. Первое подмножество называется рабочим диапазоном и определяется выражением

                                                              (1)

Многочлен A(z) с коэффициентами из поля GF(p) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона P_полн(z), то есть принадлежит рабочему диапазону . Второе подмножество GF(p^v), определяемое произведением r=n-k контрольных оснований

,                                                          (2)

задает совокупность запрещенных комбинаций. Если A(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома A(z) относительно подмножеств позволяет однозначно определить, является ли кодовая комбинация  разрешенной, или она содержит ошибочные символы.

Рассмотрим корректирующие способности кодов ПСКВ, с одним контрольным основанием. В упорядоченной системе оснований ПСКВ в качестве контрольного выбирается модуль, удовлетворяющий условно

 где i =1, 2,..., k.                                                  (3)

Считаем, что если исходные операнды  и  как и результат выполнения  арифметической операции 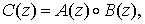  лежат внутри диапазона P_раб(z), то полином  не содержит ошибки. В противоположном случае, результат C(z) является ошибочным.

Переход из множества разрешенных комбинаций  во множество запрещенных осуществляется в результате искажения значения остатка  и преобразования его к виду . Если полином С(z) является элементом рабочего диапазона, то согласно [1], имеем

.                                                     (4)

Для упорядоченной системы оснований ПСКВ, выбор контрольного основания , удовлетворяющего (3), обеспечивает выполнение

.                                         (5)

Тогда, на основании (4) справедливо

.                                                       (6)

Но искажение остатка по i-ому основанию приводит к тому, что полином C(z) не может находиться в интервале . Следовательно

.                                                      (7)

Тогда, исходя из (6), получаем . Следовательно, полином С*(z) не принадлежит  P_раб(z), и он содержит ошибку.

Теорема. Если в упорядоченной системе оснований p₁(z),...,p_k+1(z) ПСКВ расширенного поля Галуа GF (2^ν) полином , то модулярный код данного полинома содержит как минимум одну ошибку.

Доказательство. Положим, что С*(z) не содержит ошибки. Согласно китайской теореме об остатках имеем

.   (8)

В то же время, согласно теореме, приведенной в [3] существует элемент последовательности C_IR(z), который отличается от C*(z) значением по i-ому основанию  и принадлежит Р_раб (z).

.   (9)

Следовательно

.                            (10)

Подставим (8) и (9) в равенство (10) и, преобразовав их с учетом

  ,    (11)

получаем

.      (12)

Равенство (12) выполняется при условии , т.е. когда .Но согласно, исходным данным . Следовательно, С*(z) содержит ошибку по i-ому основанию полиномиальной системы классов вычетов. Доказательство закончено.

Благодаря представленной теореме, была установлена возможность применения избыточных кодов ПСКВ для процедур поиска и коррекции ошибок.

СПИСОК ЛИТЕРАТУРЫ:

1. Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
2. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68.
3. Калмыков И.А., Щелкунова Ю.О., Гахов В.Р., Шилов А.А. Математическая модель коррекции ошибок в полиномиальной системе класса вычетов на основе определения корней интервального полинома/Волновые процессы. №5, т.6, Самара, 2003 - С.30-34.
4. Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.

Библиографическая ссылка