Поэтому имеет смысл провести системный анализ газодобычи, с помощью имитационного моделирования долгосрочного планирования добычи газа решать различные экстремальные задачи, используя методы теории оптимального управления [1] и вывести аналитическую зависимость максимизируемых (минимизируемых) функционалов от управляющих параметров. С помощью этих моделей можно решать, например, задачи о максимизации накопленной добычи, прибыли, а также периода максимальной добычи, наибыстрейшего достижения заданного уровня добычи и другие.
Рассмотривается модель группы газовых месторождений.
Пусть имеется m месторождений, в каждом из которых динамику основных технологических показателей можно описать системой трех дифференциальных уравнений, содержащих управление n(t) - число новых скважин, вводимых в строй в течение одного года.
i - индекс месторождения, количество месторождений 
Добыча газа на i-м месторождении равна произведению фонда скважин Ni на дебит qi :
Qi=Niqi (1)
Месторождения связаны между собой общим ограничением на капитальные вложения в строительство скважин:
(2)
общим ограничением на объем добычи газа по району
(3)
В формулах (2), (3) ci - стоимость строительства скважины на i-м месторождении; K(t) - максимально возможные капитальные вложения, выделяемые в году t на строительство скважин; П(t) - план добычи газа по району.
Ставится следующая оптимизационная задача на конечном отрезке времени:
(4)
при 
(5)
(6)
(7)
(8)
(9)
(10)
Заметим что 
(11)
Для решения данной оптимизационной задачи применяется метод В.Ф. Кротова[2]. Для задачи минимизации I, где J=-I, составим конструкцию:
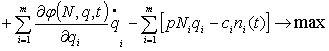
Далее, используя метод множителей Лагранжа, получим
R1 =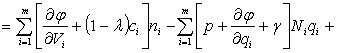 
где 
- множители Лагранжа.
Полагая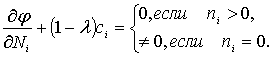 
и после несложных преобразований получим выражение для φ(N, q, t).
Рассмотрев отдельно уравнение (6) при заданных краевых условиях получим ni(t) и соответствующую траекторию Nit (при , 
).
Рассмотрев уравнение (5), применив полученное выражение для Ni(t), получим qi(t). Выражение для R1 примет вид:
при подстановке Ni(t) и qi(t), .
Полагая 
и 
получили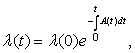 
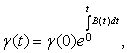
где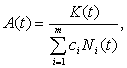 
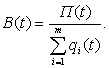
причем должно быть 
Множители Лагранжа, как правило, определяют объективно-обусловленные оценки, т.е. соответствующих оптимальных цен.
Заметим, что если 
т.е. 
то 
и должно быть 
но это всегда возможно.
Таким образом, в данной работе для создания имитационной модели оптимального управления группой газовых месторождений при помощи метода В.Ф. Кротова найдены составляющие для максимизируемого функционала, зависящего от управляющих параметров.
Литература:
- Мергулов Р.Д., Хачатуров В.Р., Федосеев А.В. Системный анализ в перспективном планировании добычи газа. М.: Недра, 1992. 287 с.
- Основы теории оптимального управления. Под ред. В.М. Кротова. М.: Высшая школа, 1990. 430 с.
- Бияров Т.Н. Теория устойчивости движения на конечном отрезке времени. Алма-Ата, 2003. 290 с.
Работа представлена на III научную международную конференцию «Актуальные проблемы науки и образования», ВАРАДЕРО (Куба), 19-29 марта 2008г. Поступила в редакцию 25.02.2008г.
Библиографическая ссылка
Коспанова К. К. СОЗДАНИЕ ИМИТАЦИОННОЙ МОДЕЛИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ГРУППОЙ ГАЗОВЫХ МЕСТОРОЖДЕНИЙ // Современные наукоемкие технологии. – 2008. – № 5. – С. 83-85;URL: https://top-technologies.ru/ru/article/view?id=23880 (дата обращения: 23.11.2024).