Во-первых, отказавшись от измерения скорости, и обратившись вместо этого к более тонким моделям взаимодействия, мы получаем возможность оценивать не реализованную фактически систему, а ее идею, замысел, логику. Это дает колоссальный выигрыш в проектной деятельности, так как тестирование системы выносится на самые ранние этапы разработки, что существенно снижает затраты, более того - результаты измерений порой подсказывают новое удачное решение для последующих этапов.
Во-вторых, наши измерения юзабилити можно вообще не соотносить с каким-либо конкретным проектом. Измеряя не интерфейс проекта, а интерфейсную схему, мы получаем возможность внедрять ее в различные параллельные, с точки зрения решаемых задач, проекты, причем, повторное тестирование уже не требуется.
И, наконец, наш метод изящен и прост. Специалист, владеющий им, может провести исследование «на салфетке за завтраком», подтверждая мысль о том, что истинное мастерство экспериментатора - не в применении специальной аппаратуры, а в умении смоделировать изучаемое явление.
Диаграммы сценариев
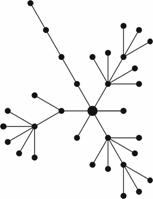
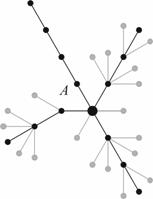
Набор состояний интерфейса естественно описывается в виде графа, вершинами которого являются состояния системы, а ребрами - возможные действия пользователя в том или ином состоянии. Граф состояний редуцируется исключением всех путей после неверного в рамках решения данной задачи выбора и в результате получается так называемая диаграмма состояний (см. рис. 1.a), которая все еще содержит как верные, так и неверные сценарии решения задачи. Мы помечаем неверные выборы пользователя серым цветом, выделяя, таким образом, траектории верных сценариев решения задачи, и получаем диаграмму сценариев (см. рис. 1.b).
Каждое действие испытуемого кодируется одной буквой, и, тем самым, траектория его движения по интерфейсу описывается последовательностью букв, «словом». Спектр выборов в каждом состоянии мы кодируем латинскими буквами, начиная с A, совершая обход по часовой стрелке в алфавитном порядке. Таким образом, для однозначного описания любой траектории достаточно отметить начальную точку A на дуге стартовых выборов (см. рис. 1.b).
На диаграмме, представленной выше (см. рис. 1.b), успешные сценарии кодируются следующим образом: AAAA, BCB, DCB, FAC. К неудачным сценариям можно отнести: BA, C, DCC, и т. д. Всего неудачных сценариев 19 - столько, сколько имеется на диаграмме финишных серых точек. Успешных сценариев 4 - ровно столько имеется на диаграмме финишных черных точек.
|
|
|
|
a. Диаграмма состояний |
b. Диаграмма сценариев |
Рис. 1. Диаграммы интерфейса
Для проведения эксперимента экраны системы имитируются бумажными распечатками, которые готовятся на базе диаграммы сценариев: каждому состоянию отвечает один лист, содержащий список интерфейсных указаний. Таким образом, каждый лист соответствует состоянию диаграммы, а его содержание - действиям, возможным в данном состоянии. Это и есть материалы для игры, в которую модератор эксперимента будет играть с каждым из испытуемых.
Игра
В эксперименте участвуют два человека: испытуемый и модератор. Модератор знает диаграмму сценариев. Он знает, в чем состоят успешные сценарии, то есть, какие действия в каждом из состояний являются верными, а какие - нет, испытуемый этого не знает. От испытуемого требуется решить поставленную перед ним задачу всеми возможными способами, начиная с наиболее естественных, на его взгляд, сценариев, и заканчивая самыми экзотическими, затратив на это наименьшее количество действий.
Каждое действие испытуемого может быть верным или неверным. Если испытуемый совершает неверное действие, модератор сообщает ему об этом, и испытуемый выполняет очередную попытку. Если он совершает верное действие, модератор также сообщает ему об этом, но испытуемый понимает, что это не единственно верное действие, так как он знает, что в любой ситуации, как правило, имеется несколько верных решений. Когда испытуемый достигает цели, модератор возвращает его в исходное состояние, после чего он пытается найти новое решение.
В конце концов, наступает момент, когда испытуемый считает, что он предложил уже достаточное число различных решений, и других решений нет, или, может быть, они имеются, но он не считает их разумными. Тогда он сообщает об этом модератору, и игра прекращается.
Протокол
Действия модератора не ограничиваются предъявлениями листов состояний и сообщениями об ошибках. Помимо игры с испытуемым модератор ведет протокол ее хода, в который вносит все выборы испытуемого, с указанием их верности и того порядка, в котором они выполнялись. Именно эти цепочки действий и есть предмет последующего анализа, именно они и описывают манеру взаимодействия пользователя с изучаемой интерфейсной системой.
Каждое действие пользователя кодируется одной буквой в соответствии с диаграммой сценариев. Цепочка букв образует последовательность действий, которая и складывается в успешный сценарий. По ходу игры испытуемый ошибается, то есть, выполняет неверные действия, которые также кодируются при помощи диаграммы (но, в отличие от верных действий не прописными, а строчными буквами) и, также как и верные, заносятся в протокол.
Например, отталкиваясь от данной выше диаграммы сценариев (см. рис.1.b), мы могли бы получить следующий экспериментальный протокол:
1 сценарий - AAAA,
2 сценарий - BaCB,
3 сценарий - DbCB,
4 сценарий - eBedCB (повтор сценария 2),
безуспешные попытки - eFa.
Мы видим, что наиболее естественным испытуемому представляется сценарий в направлении A. Выполняя, другие сценарии, в направлении B и D, испытуемый допускает ошибки. Сценарий в направлении B испытуемый повторяет дважды, а сценарий в направлении F - вообще не обнаруживает.
Числовые характеристики интерфейса
Игровая экспериментальная процедура позволяет на базе имеющихся экспериментальных протоколов получить сразу несколько характеристик интерфейса, среди которых отметим две числовые: длину пути S и степень ошибочности P.
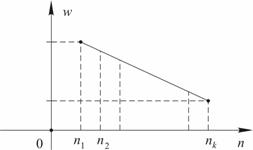
Начнем с длины пути. Проще всего определить ее как среднее арифметическое длин всех теоретически возможных сценариев, приводящих к решению данной задачи. Однако из имеющегося набора возможных удачных сценариев пользователь может знать лишь о некоторых, а использовать - вообще, лишь один или два. Длины именно этих, активно используемых, сценариев мы и должны учитывать в первую очередь. Пусть на реализацию первого обнаруженного им сценария испытуемый затратил n1 действий, включая ошибочные, на реализацию второго n2 и т. д. Каждой длине ni мы будем приписывать определенный вес wi, рассматривая его как вероятность того, что в реальной ситуации испытуемый воспользуется тем или иным сценарием. Эти вероятности распределены не равномерно: ранним сценариям отвечают большие вероятности, а поздним - меньшие (см. рис. 2.b). Первому из сценариев мы приписываем наибольший вес, а последнему - наименьший, предполагая, что следующий за последним сценарий обладает нулевым весом, а интерполяция всех промежуточных весов линейная[2].
Нетрудно вывести формулу для веса очередного сценария и применить весовые коэффициенты к вычислению средней длины пути:
![]() , где
, где ![]() .
.
Это и есть рабочая формула для вычисления длины пути. Здесь ni - число действий, затраченных испытуемым на реализацию i-го сценария (включая как продуктивные, так и ошибочные), а wi - вес соответствующего сценария, вычисленный в соответствии с его порядковым номером.
|
|
|
|
a. Равномерное распределение весов |
b. Неравномерное распределение весов |
Рис. 2. Веса сценариев
Наряду с длиной пути, имеется еще один важнейший показатель эффективности интерфейса: то, насколько часто в обращении с ним пользователь допускает ошибки. Этот показатель мы будем называть степенью ошибочности, и определим его как отношение числа ошибочных действий к общему числу действий, совершенных испытуемым, включая как продуктивные, так и ошибочные[3]:
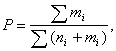
где ni - число продуктивных действий i-го сценария, mi - число ошибок, допущенных испытуемым при реализации i-го сценария, суммирование ведется до k, где k - число обнаруженных испытуемым успешных сценариев.
В приведенном выше примере испытуемый обнаружил три успешных сценария: сначала - в направлении A, затем - в направлении B, и, наконец, - в направлении D. Их веса таковы:
![]() ,
,![]() ,
,![]() .
.
На реализацию первого сценария испытуемый затратил 2 действия[4]. На реализацию второго - 4 действия, среди которых было одно ошибочное. И, точно так же, на реализацию третьего у него ушло 4 действия, среди которых было одно ошибочное. Таким образом,
![]() ,
,
то есть, в среднем на реализацию этого сценария испытуемый тратит 3 действия[5]. Вторая числовая характеристика интерфейса, степень ошибочности, вычисляется как отношение числа ошибочных действий к общему числу действий, выполненных пользователем:
![]() .
.
Статистический анализ
Таким образом, игровой эксперимент дает исследователю двумерный массив числовых данных Si, Pi, к которым применим весь спектр известных статистических методов: от доверительной оценки параметров распределений до (если речь идет о сравнительном анализе двух или более интерфейсных схем) определения достоверности сдвига среднего при помощи соответствующих статистических критериев: Розенбаума, Манна-Уитни и т. д. (см. например, [2], где дан подробный обзор этих методов).
СПИСОК ЛИТЕРАТУРЫ:
- 1. Раскин, Дж. Интерфейс: новые направления в проектировании компьютерных систем/ М., С-Пб.: Символ, 2006- 268 с.
- 2. Сидоренко, Е.В. Методы математической обработки в психологии/ С-Пб.: Речь, 2004- 350с.
[1] Исключение составляют лишь методы, базирующиеся на модели скорости печати GOMS (см., например, [1], где, помимо прочего, дан беглый обзор этих методов). Однако методы GOMS вообще игнорируют поведение пользователя, оперируя исключительно с числовыми характеристиками ввода данных, и мы относим их, скорее, к спектру теоретических схем, нежели к практическому инструментарию.
[2] На самом деле зависимость веса от номера вряд ли является строго линейной. Скорее всего, она носит либо экспоненциальный характер, если кривая зависимости выпукла вниз, либо логарифмический, если кривая выпукла вверх. Точное определение интерполяционной зависимости - это отдельная очень сложная задача, решение которой не входит в наши планы. Однако даже линейная интерполяция неравномерного распределения весов гораздо точнее отражает действительность, нежели предположение его равномерности.
[3] Отметим, что мы могли бы определить степень ошибочности по-другому: как отношение числа ошибочных действий к числу продуктивных. Это тоже разумно, но тогда мы могли бы получить ситуацию, когда число ошибок превышает число продуктивных действий, и степень ошибочности оказывается больше единицы. Гораздо удобнее иметь в своем распоряжении нормированные величины, заведомо заключенные между 0 и 1.
[4] Циклы действий, не требующих выбора, мы рассматриваем как одно действие. То есть, в направлении A испытуемый бездействовал, начиная со второго шага.
[5] Если бы мы использовали среднее арифметическое для вычисления длины пути, мы получили бы большее значение: S=3,33.
Библиографическая ссылка
Мосин В.Г. МЕТОД ИГРОВОЙ ОЦЕНКИ ЮЗАБИЛИТИ // Современные наукоемкие технологии. 2008. № 4. С. 20-24;URL: https://top-technologies.ru/ru/article/view?id=23725 (дата обращения: 07.03.2026).