На современном этапе развития космической техники важную роль для исследования различных научных и социально-экономических проблем играют космические аппараты дистанционного зондирования Земли. Опыт использования таких КА («Океан-О», "Метеор-3М", «Фотон-М» и др.) по целевому применению показал высокую эффективность решения задач в областях природопользования, материаловедения, биологии, экологического мониторинга и в других областях.
В настоящей работе представлены результаты математической формализации процессов функционирования ЦУП как БСУ. Такая формализация дает возможность на основе анализа альтернативных вариантов структуры выявить организационные и технические ресурсы и выработать требования к оптимальной структуре ЦУП.
2. Выделение иерархических уровней ЦУП как БСУ
Известны два основных подхода к синтезу иерархических БСУ. При первом - структура иерархической системы считается заданной. На ее основе производится оптимизация распределения функций, выполняемых отдельными узлами; а также согласование целей и оптимизация взаимодействия узлов различных уровней. При втором - структура определяется в результате синтеза основных или одной ведущей функции, например, функции планирования или оперативного управления.
Представляется перспективным итерационное исследование структуры БСУ. При этом используется комбинация из двух подходов. На первом этапе структура иерархической системы считается заданной и проводится оптимизация распределения выполняемых функций по отдельным элементам системы, а также согласование целей и оптимизация взаимодействия подсистем различных уровней иерархии. На втором этапе проводится предварительный анализ альтернативных вариантов структурного построения системы. При этом, в результате синтеза ведущих функций управления определяется оптимальная структура БСУ.
При построении моделей функционирования ЦУП КА реализуется общие закономерности структурного построения иерархических систем управления:
- последовательное вертикальное расположение подсистем, составляющих соответствующую соподчиненность;
- приоритет действий или право «вмешательства» подсистемы верхнего уровня в действия подсистем нижнего уровня;
- зависимость действий подсистемы верхнего уровня от фактического исполнения своих функций подсистемами нижнего уровня;
- значительно большая степень неопределенности в описании задач управления на верхних уровнях иерархии.
Анализ процессов функционирования элементов ЦУП как БСУ в процессе управления автоматическими КА позволяет выявить основные иерархические уровни:
- верхний уровень (уровень координации) - реализует координацию всех действий по управлению КА с целью наиболее эффективного выполнения программы полета КА;
- второй уровень (уровень самоорганизации) - реализует выбор критериев и алгоритмов, используемых на нижних уровнях иерархии с целью обеспечения решения главных задач управления;
- третий уровень (уровень адаптации) - осуществляет конкретизацию множеств неопределенностей для подсистем верхних уровней путем анализа текущей ситуации и выработки требований к алгоритмам решения задач подсистемами нижнего уровня;
- четвертый уровень (уровень выбора) - осуществляет решения частных задач в соответствии с исходными данными и алгоритмическими предписаниями от подсистем высшего уровня.
3. Математическая формализация функционирования ЦУП как БСУ на основе методов теории массового обслуживания
Основная сложность, ограничивающая применение этих методов, связана с тем, что в реальных условиях практически не существует марковских процессов, переводящих систему из одних состояний в другие. Применяемость методов теории марковских процессов определяется тем, к каким ошибкам в предельных вероятностях системы может привести формальная замена реальных процессов марковскими (или реальные потоки пуассоновскими).
В теории массового обслуживания известен метод последействия когда отличающиеся от пуассоновских реальные потоки апроксимируются потоками Эрланга и в схему возможных состояний системы вводятся некоторые фиктивные «псевдосостояния».
В рамках настоящей работы ограничимся формальным допущением о том, что процессы функционирования в системе ЦУП-БСУ являются марковскими, и на основе этого формализуем рассматриваемую задачу, используя методы теории массового обслуживания.
Дадим определение элементам пространства состояний ЦУП как БСУ на основе приведенной ориентировочной схемы взаимодействия отдельных элементов четырехуровневой иерархической системы (граф 1).
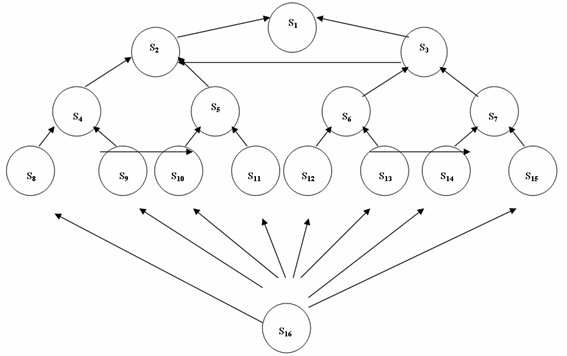
Граф 1. Схема взаимодействия отдельных элементов системы.
Опишем элементы графа состояния согласно приведенному рисунку:
S1 - выполнение программы полета; S2 - решение задач планирования работы бортовых систем; S3 - выдача оперативных командных воздействий на основе анализ состояния бортовых систем; S4 - решение задач баллистико-навигационного обеспечения полета; S5 - формирование массивов командно-программной информации; S6 - диагностика состояния бортовых систем; S7 - выработка рекомендаций по управлению бортовыми системами; S8 - прием и обработка измерений текущих навигационных параметров; S9 - определение задействованных средств наземного комплекса управления; S10 - прием и обработка исходных данных Главного оператора; S11 - прием и обработка исходных данных разработчиков бортовых систем; S12 - прием и обработка телеметрической информации; S13 - прием и обработка информации оперативного контроля; S14 - проверка правильности выдачи командных воздействий; S15 - предварительный прогноз состояния бортовых систем; S16 - исходное состояние.
При этом, переходы системы из состояния S16 в состояния S8, S9, S10, S11, S12, S13, S14, S15 соответствуют функционированию элементов четвертого уровня иерархии системы (уровня выбора). Последующие переходы системы в состояния S4, S5, S6, S7 соответствуют работе элементов третьего уровня (уровня адаптации); переходы в состояния S2 и S3 - работе элементов второго уровня (уровня самоорганизации); переходы в состояние S1 - работе верхнего уровня (уровня координации).
Схему, представленную на рис. 1 можно интерпретировать как граф состояний ЦУП с иерархической структурой. Процесс функционирования системы начинается из исходного состояния S16 и, переходя через промежуточные состояния Si, завершается выполнением программы полета (состояние S1).
Обозначим Рi (i = 1, ...16) вероятность нахождения системы в состоянии Si. Нетрудно видеть, что в начальный момент времени t0:
P16(t0) = 1, Pi(t0) = 0 при i ≠ 16. (1)
Для представленного графа состояний значения вероятностей Pi определяются системой дифференциальных уравнений Колмогорова:
![]()
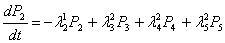
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
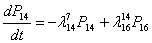
![]()
![]() (2)
(2)
Интенсивности потоков событий ![]() будем определять как скорость выполнения операций, необходимых для перевода системы из состояния i в состояние j. Например,
будем определять как скорость выполнения операций, необходимых для перевода системы из состояния i в состояние j. Например, ![]() - отношение объема выполняемых операций по диагностированию состояния бортовых систем, необходимого для завершения анализа их работоспособности ко времени выполнения работ.
- отношение объема выполняемых операций по диагностированию состояния бортовых систем, необходимого для завершения анализа их работоспособности ко времени выполнения работ.
При этом, допускаются вариации значений ![]() в диапазоне ± 20% от номинальных значений. Отметим, что определение
в диапазоне ± 20% от номинальных значений. Отметим, что определение ![]() осуществлялось в предположении отсутствия случайных возмущающих факторов, которые могут привести к существенному изменению динамки выполнения операций: неисправности работы технических средств, ошибки персонала управления и т.д.
осуществлялось в предположении отсутствия случайных возмущающих факторов, которые могут привести к существенному изменению динамки выполнения операций: неисправности работы технических средств, ошибки персонала управления и т.д.
В качестве критерия решения вариационной задачи будем использовать минимум времени перевода системы в состояние S1, т.е.
TΣ = min при Р1 (Т) = 1 (3)
С учетом вышеизложенного сформулируем вариационную задачу: для системы дифференциальных уравнений (2) требуется определить совокупность интенсивностей переходов ![]() , изменяющихся в пределах ± 20% относительно своих номинальных значений обеспечивающую перевод системы из начального состояния (1) в конечное (3).
, изменяющихся в пределах ± 20% относительно своих номинальных значений обеспечивающую перевод системы из начального состояния (1) в конечное (3).
4. Анализ полученных результатов
Дадим описание вычислительному процессу решения сформулированной вариационной задачи.
Представляет интерес оценить частные влияния вариаций ![]() относительно номинальных значений на время ТΣ. В результате проведения расчетов показано, что все интенсивности переходов
относительно номинальных значений на время ТΣ. В результате проведения расчетов показано, что все интенсивности переходов ![]() можно разделить на две категории. К одной категории относятся такие
можно разделить на две категории. К одной категории относятся такие ![]() , увеличение значений которых приводит к снижению времени Т∑. Для рассматриваемого примера это
, увеличение значений которых приводит к снижению времени Т∑. Для рассматриваемого примера это ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . Вариации остальных 14-ти значений :
. Вариации остальных 14-ти значений : ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,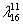 ,
,![]() ,
,![]() ,
,![]() - не влияют на значение ТΣ. Показано, что при увеличении значений
- не влияют на значение ТΣ. Показано, что при увеличении значений ![]() из первой категории на 20% относительно номиналов, время ТΣ снижается до 51 минуты 25 секунд, что ≈ на 18,5% меньше рассчитанного ранее суммарного времени перехода.
из первой категории на 20% относительно номиналов, время ТΣ снижается до 51 минуты 25 секунд, что ≈ на 18,5% меньше рассчитанного ранее суммарного времени перехода.
Следует отметить, что повышение оперативности решения отмеченных первоочередных задач может быть обеспечено не только за счет роста интенсивности их выполнения, но и за счет изменения структурного состава иерархических БСУ.
5. Заключение
Представленный математический аппарат принципиально может быть использован для исследования быстродействия альтернативных вариантов структурного построения иерархических систем ЦУП как БСУ. При этом, осуществляется не только сравнительная оценка быстродействия альтернативных вариантов, но и для каждого варианта определяются критические звенья системы.
Дальнейшее развитие предложенного в работе методологического подхода связано, в первую очередь, с уточнением математических моделей функционирования ЦУП-БСУ за счет использования метода «псевдосостояний», с учетом влияния на систему непрогнозируемых случайных возмущающих факторов, а также, с возможностью одновременного функционирования нескольких БСУ при использовании обобщенного критерия минимизации времени выполнения целевой функции совокупностью всех систем.
Практическая значимость предлагаемого математического аппарата связана с необходимостью решения проблемы создания компактных, рентабельных, высокотехнологичных структур управления различными КА НСЭН, запуск которых планируется в 2008-2009 гг. Внедрение в практику проектирования общей структуры ЦУП КА НСЭН разработанного методологического подхода может обеспечить снижение потребных финансовых затрат на создание аппаратно-программных средств управления каждым последующим КА НСЭН.
СПИСОК ЛИТЕРАТУРЫ:
- Месарович М., Такахара И. Теория иерархических многоуровневых систем. М.: Мир, 1973 г.
- Соколов Н.Л., Поздняк Т.И., Пинчук В.Б. К вопросу об использовании теории марковских процессов для исследования движения КА в атмосфере. Космические исследования, 1990 г., т. 28, № 3.
- Денисов А.А., Колесников Д.Н. Теория больших систем управления. Л.: Энергоиздат, 1982 г.
- Венцель Е.С. Исследование операций. М.: Советское радио, 1982 г.
Работа представлена на VII научную международную конференцию «Современные наукоемкие технологии», Хургада (Египет), 22-29 февраля 2008 г. Поступила в редакцию 04.02.2008.
Библиографическая ссылка
Соколов Н.Л., Селезнева И.А. СОЗДАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ФУНКЦИОНИРОВАНИЯ ЦЕНТРА УПРАВЛЕНИЯ ПОЛЕТАМИ В ПРОЦЕССЕ ЭКСПЛУАТАЦИИ КОСМИЧЕСКИХ АППАРАТОВ И ПОЛУЧЕНИЯ ЦЕЛЕВОЙ ИНФОРМАЦИИ // Современные наукоемкие технологии. 2008. № 3. С. 56-59;URL: https://top-technologies.ru/ru/article/view?id=23326 (дата обращения: 28.12.2025).



