Если к материалу приложить разность потенциалов U, по которому течет ток I, то сопротивление проводника определяется по формуле R = U / I.
В свою очередь сопротивления проводника длиной l и площадью поперечного сечения S определяется зависимостью R = ρl / S, где коэффициент пропорциональности с является удельным сопротивлением.
Поскольку кинетическая энергия электронов при прохождении зарядом dq разности потенциалов U записываются в виде dE = Udq. Разделим теперь обе части этого выражения на dt и получим 
, где P = UI - потери электрической мощности или джоулевы потери можно записать как P = I2R, которая преобразуется в тепло. При подстановке сопротивления получим: P = I2ρl / S . На элементе длины dl выделяется мощность 
, при площади полусферы 
радиусом l это выражение запишется 
. Проинтегрируем 
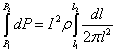, получим:
.
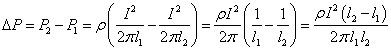Из этой зависимости видно, что потери мощности, а, следовательно, тепловыделение пропорционально силе тока в квадрате и наиболее интенсивное тепловыделение будет происходить в месте контакта и затем, по мере углубления, резко падать. В пределе при l2→∞ получим, что 
.
Таким образом, полученная математическая модель тепловыделения, возникающего при электромеханическом воздействии на материал, позволяет изучить особенности изменения температурных полей, которые в дальнейшем могут использоваться в расчетах, связанных с определением геометрии и расположения структурных зон напряженно-деформированного состояния обрабатываемого материала и других параметров.
Библиографическая ссылка
Гришин О.П., Гришина Е.В., Настин А.А., Исаев Ю.М. ВЫДЕЛЕНИЕ ТЕПЛА ТОЧЕЧНЫМ ИСТОЧНИКОМ ТОКА В ПЛАСТИНЕ // Современные наукоемкие технологии. – 2008. – № 3. – С. 50-50;URL: https://top-technologies.ru/ru/article/view?id=23317 (дата обращения: 20.04.2024).