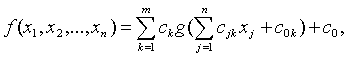Альтернативным методом моделирования являются искусственные нейронные сети (НС). НС являются математическим аналогом биологических нейронов мозга. НС можно рассматривать как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. Эти модели различаются по строению отдельных нейронов, по топологии связей между ними и по алгоритмам обучения.
Существуют некоторые рекомендации относительно необходимой топологии нейронной сети, позволяющие использовать их для решения задач моделирования. В основе этих рекомендаций лежит фундаментальная для теории нейронных сетей теорема А.Н. Колмогорова и В.И. Арнольда о представлении непрерывных функций многих переменных в виде суперпозиции непрерывных функций одной переменной и сложения:
|
|
(1) |
где gk и hjk - некоторые функции одной переменной.
А Теорема Хехт-Нильсена доказывает представимость функции многих переменных достаточно общего вида с помощью двухслойной нейронной сети с прямыми полными связями с n нейронами входного слоя, (2n+1) нейронами скрытого слоя с заранее известными ограниченными функциями активации (например, сигмоидальными) и m нейронами выходного слоя с неизвестными функциями активации.
Важным следствием из теоремы Хехт-Нильсена является представимость любой многомерной функции нескольких переменных с помощью нейронной сети фиксированной размерности. Неизвестными остаются следующие характеристики функций активации нейронов. Про функции активации нейронов выходного слоя из теоремы Хехт-Нильсена известно только то, что они представляют собой нелинейные функции общего вида. В одной из работ, продолжающих развитие теории, связанной с рассматриваемой теоремой, доказывается, что функции активации нейронов выходного слоя должны быть монотонно возрастающими. Это утверждение в некоторой степени сужает класс функций, которые могут использоваться при реализации отображения с помощью двухслойной нейронной сети. На практике требования теоремы Хехт-Нильсена к функциям активации удовлетворяются следующим образом. В нейронных сетях как для первого (скрытого), так и для второго (выходного) слоя используют сигмоидальные передаточные функции с настраиваемыми параметрами. То есть в процессе обучения индивидуально для каждого нейрона задается максимальное и минимальное значение, а также наклон сигмоидальной функции. Т.о. из объединенной теоремы Колмогорова-Арнольда-Хехт-Нильсена следует, что для любого алгоритма существует НС, которая его реализует. Что говорит о том, что НС является универсальным вычислительным средством для аппроксимирования функций.
Позже было доказано, что двухслойная нейронная сеть, описываемая выражением
|
|
(2) |
где g(z) = 1/(1 + exp(-z)), способна аппроксимировать с любой точностью любую непрерывную функцию многих переменных. Эта сеть имеет n входных, 2n+1 скрытых и один выходной нейрон. В этом случае неопределенным остается только число нейронов первого слоя. Оно подбирается в зависимости от размерности входного и выходного сигнала, а также от числа элементов обучающей выборки.
Таким образом, приведенные рекомендации позволяют облегчить построение нейронных сетей и тем самым успешно применять их в решении задач моделирования технологических процессов.
Библиографическая ссылка
Бахметова Н.А., Токарев С.В. МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ С ПОМОЩЬЮ НЕЙРОННЫХ СЕТЕЙ // Современные наукоемкие технологии. 2008. № 2. С. 139-140;URL: https://top-technologies.ru/ru/article/view?id=23277 (дата обращения: 05.03.2026).




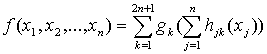 ,
,