Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Бабин А.И.

Статья в формате PDF

167 KB

Рассмотрим сначала решение задачи при условии, что изменение количества ПА внутри зоны обслуживания много меньше изменения количества требований на обслуживание. Такая постановка адекватна ситуации в СПР радиально-зоновой архитектуры. Сделаем несколько естественных допущений:

1. Количество объектов в среднем пропорционально площади территории на которой могут находится абоненты. Будем считать что вероятность числа объектов определяется только площадью S участка и не зависит от его формы и расположения.
2. Количество ПА на одном участке не зависит от количества ПА на любом другом участке, который не пересекается с первым.
3. Вероятность того, что на участке малой площади попадут не менее 2-х ПА пренебрежимо мало по сравнению того, что на этот участок попадет одно ПА.

Другими словами на одном малом участке больше одного ПА быть не может.

Исходя из принятых допущений легко показать, что функция P_k(S)- вероятность того, что на участок площадью S попало ровно k - ПА удовлетворяет дифференциальному уравнению:

                                                                 (1)

и определяется формулой:

                                                                    (2)

Таким образом, в условиях, когда изменение числа ПА в зоне мало по сравнению с изменением числа заявок на обслуживание, число ПА, равное k, случайно и подчинено закону Пуассона.

Состояние случайной среды в момент времени t будем характеризовать величиной n - число вызовов. Тогда, если l - число предоставленных каналов, λ  - интенсивность потока вызовов от одного ПА, μ - интенсивность потока освобождения (1/μ - средняя продолжительность разговора), то можно составить следующее уравнение отдельно для случаев n<l и n≥l .

При n< l

                                  (3)

и при n ≥l

                                    (4)

Уравнения отличаются коэффициентами "освобождения каналов" - в первом случае nμ и (n+1)μ , во втором - lμ.

Для стационарного решения уравнения приобретают вид:

для n<l:

решение которого:

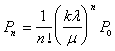 .                                                                     (5)

для n≥l уравнение:

и решение которого:

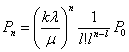                                           (6)

Условие стационарности случайной среды вытекает из обеспечивается сходимостью следующего ряда

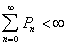,                                                                      (7)

где P_n - вероятность того, что длина очереди вызовов равна n.

С учетом (5), (6) и (7) условие стационарности или конечности очереди требований определится неравенством:

<1                                                                    (8)

Выражение для P⁰ определяется из условия нормировки

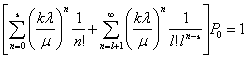                                           (9)

Если  таковы, что наименьшее l, удовлетворяющее (8), невелико, то вклад первой суммы в (9) небольшой, а вторая вычисляется по формуле бесконечно убывающей геометрической прогрессии, т.е.

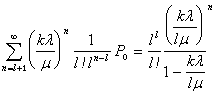                                                     (10)

Таким образом, полученные формулы определяют решение поставленной задачи при принятых ограничениях.

Рассмотрим теперь решение задачи, при условии, что изменение величины k соизмеримо с изменением величины n . В этом случае рассмотрим модель случайного процесса, описывающего состояние системы в виде двумерного марковского процесса с состояниями определяемыми параметрами (k,n).

Пусть P _k,n (t) - вероятность того, что в момент времени t процесс находится в состоянии c параметрами (k,n), где k - число ПА в зоне, n - число заявок. ПА въезжают и выезжают из зоны. Плотности потоков въезда и выезда должны быть такими, чтобы среднее число машин в зоне не стремилось к бесконечности (при неограниченном числе ПА). Будем считать, что эти плотности совпадают и равны q. Плотность потока вызовов в момент t пропорциональна числу ПА в зоне за вычетом ПА уже вышедших на связь в момент времени t и равна λ(k-n). Плотность освобождения каналов (в случае их бесконечного числа) пропорциональна числу занятых μn. Если число каналов ограничено, то при n≥l плотность освобождения каналов пропорциональна μl. Вероятность отсутствия ПА в зоне зависит от всех вышеперечисленных факторов и определяется из условия нормировки:

,                                                                           (11)

где N равно либо бесконечности в предположении неограниченного числа ПА либо максимально возможному числу абонентов.

Учитывая вышесказанное, можно составить следующее дифференциально-разностные уравнения:

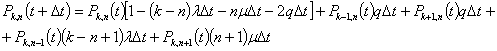        (12)

Считается, что попасть в состояние k,n из состояний более далеких h,m является величиной 0(Δt ), где |k-h|>1 и (или) |n-m|>1.

Уравнение (12) составлено для неограниченного числа каналов, используемых ПА. Когда же количество каналов ограничено величиной l, то уравнение (12) для n≥l будет выглядеть следующим образом:

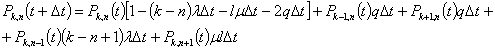       (13)

Переходя стандартным образом в (12) и (13) к дифференциальному уравнению и рассматривая стационарные случаи , получаем следующую систему линейных уравнений относительно величин P _i,j (предположение  обуславливает независимость от времени искомой вероятности, поэтому в дальнейшем будем писать ее без указания параметра t:

 для n ≤ l

 (14)

и для n≥ l

               (15)

Системы уравнений (14), (15) совместно с уравнением (11) образуют линейную систему  уравнений относительно  искомых вероятностей P _i,j  причем P _i,j= 0 для i<0, j<0 и i<j. Существование решений гарантируется ограниченностью снизу по абсолютной величине определителей ||A||:

- для неограниченного числа каналов

,

где ,

- для числа каналов ограниченных величиной l

,

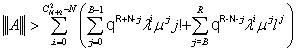где .

В качестве примера проиллюстрируем, как запишется система уравнений для N=4:

,                                                    (16)

где  = (I,0,0,0,0,0,0,0,0,0,0,0,0,0,0),

,

где , , , ,

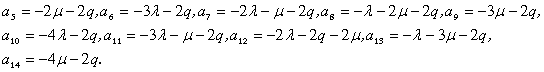
Вектор искомых вероятностей определяется соотношением

                                                                                    (17)

Библиографическая ссылка