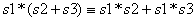
![]()
![]()
The choice of a better form for a given term is not unique and is ruled by heuristic algorithms. Besides, we create a database of elementary types of equations like the following:
![]() (1)
(1)
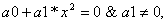 (2)
(2)
![]() (3)
(3)
Each type (i) containing in the database of elementary types is connected with a procedure Decision_i which obtaining term T expressing the given equation forms an array of answers X. In our system we write down such procedures manually but without principal problems such procedure can be created automatically from given formulas expressing values of variables as arithmetic functions of equation´s coefficients. When the type of an equation is determined as corresponding to case i of this database, procedure Decision_i is started to find the solution of the equation.
Let us consider a CBR approach on the example of square equation ![]() . This equation is transformed using an equivalence
. This equation is transformed using an equivalence ![]() , that is,
, that is, 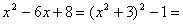
![]() , and the latter is classified as corresponding to a known type and solved by the appropriate procedure. This equation and the sequence of actions leading to the solution is added to the database of cases and in future will be used to decide square equations. We note that such approach allows us to extend easily the class of solvable equations and overcome systems like Maple in many special cases of equations.
, and the latter is classified as corresponding to a known type and solved by the appropriate procedure. This equation and the sequence of actions leading to the solution is added to the database of cases and in future will be used to decide square equations. We note that such approach allows us to extend easily the class of solvable equations and overcome systems like Maple in many special cases of equations.
References
- Case-Based Reasoning Technology: From Foundations to Applications, Mario Lenz, Brigitte Bartsch-Sporl, Hans-Dieter Burkhard, Stefan Wess, Lecture Notes in Artificial Intelligence (2005).
- Kolodner J. An introduction to case-based reazoning. Artificial Intelligence Review 6(1), 1992, 3-34.
- A.Aamondt, E. Plaza. Case-based Reazoning: Foundational Variations, and System Approaches, Published in A.Aamondt, E. Plaza (1994); AICom-Artificial Intelligence Communications, IOS Press. 7:1 (1994) 39-59.
- John R.Anderson. Cognitive Psychology and its Applications, Worth Publishers, (russ. trans. Piter Press, 2002).
[1] The second author was supported by RFBR grant РФФИ 05-01-00605а
Библиографическая ссылка
Chesnokov S., Ishmukhametov S., Rubtsova R SOLVING ALGEBRAIC EQUATIONS ON A COMPUTER // Современные наукоемкие технологии. 2006. № 6. С. 49-50;URL: https://top-technologies.ru/ru/article/view?id=22850 (дата обращения: 08.01.2026).



