Проблемы, возникающие при анализе явления удара, снижения его и другие аспекты изложены в работах [4,5,6] и др.
В общем случае направляющие - это устройство, обеспечивающие с определённой точностью и неизменностью прямолинейное движение пильной рамки. Анализ конструкций направляющих, проведённый нами по источникам отечественных и зарубежных публикаций, а также с учётом патентных материалов показывает, что каждая направляющая выполнена в виде балки, установлена на станине и воспринимающей нагрузку в направлении движения, т.е. направлении действия горизонтальных сил при перекладках. Недостатком известных конструкций является слабое демпфирование ударов ползунов при перекладках их в направляющих; следствием чего является интенсивный ударный шум излучаемый лесорамой.
С целью демпфирования ударов при перекладках пильной рамки в направляющих нами предложено плоские и призматические направляющие выполнять разъёмными из двух половин, между которыми уложен демпфирующий элемент (а/с СССР №454997 и 492384).
Детальный анализ процесса соударения в реальной конструктивной схеме ползун - направляющие ЛР провести весьма затруднительно, поэтому для проведения расчёта излучаемой звуковой мощности сделаем упрощающее предположение:
- каждая направляющая имеет форму прямоугольной пластины;
- звукопередача через болтовые соединения, крепящие направляющие к боковинам рамы, не происходит;
- соударение ползуна с направляющей происходит вдоль отрезка прямой линии, равного ширине ползуна. Направляющая колеблется как пластина, подвергнутая периодическому действию внешней силы, равномерно распределённой вдоль прямолинейного отрезка на поверхности пластины.
Эти предположения позволяют использовать метод расчета излучения звука, изложенный в [4]. Отметим, что теория колебаний пластины, возбуждаемой точечной силой [4], в данном случае не применима, так как ширина ползуна и ширина направляющей (в нашем случае) примерно равны друг другу.
Внешняя сила, равномерно распределенная вдоль прямой линии на поверхности пластин, возбуждает одномерные колебания [4]. Распределение колебательной скорости можно представить в виде одномерного интеграла Фурье
![]() (1)
(1)
где ![]() (2)
(2)
- спектральная амплитуда волнового числа;
χ - пространственное волновое число колебаний.
Аналогично представляется звуковое давление [4]
![]() (3)
(3)
(ось Z направлена перпендикулярно пластине).
Функция Р (x, z) является решением волнового уравнения
![]()
где V2 - оператор Лапласа;
к - волновое число в среде перед пластиной, если к2 = χ2 + ![]() ;
;
КZ - составляющая вектора К в направлении оси Z.
При периодическом движении потенциал скорости Ф ~![]() ;
;
r¯ - радиус-вектор; тогда можно установить связь между скоростью и звуковым давлением:
![]()
Здесь ω - циклическая частота;
с - скорость волны.
По определению потенциала скорости
![]()
Граничное условие для нормальной составляющей скорости на пластине (плоскость Z = 0 - граница пластины)
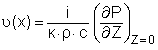
записывается через Фурье-амплитуды
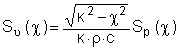
или
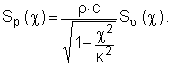 (4)
(4)
Этот переход поясним следующим образом:
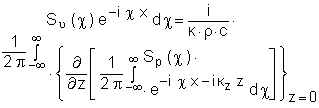
Вычислим производную по Z
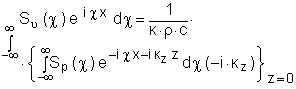
Сравним подинтегральные выражения
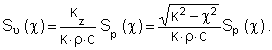
Звуковую мощность на единицу ширины длинной пластины можно выразить через Sυ (χ)
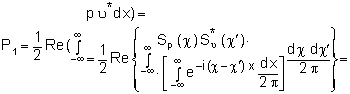
![]() (5)
(5)
Здесь использовано определение δ-функции (импульсивной функции) и ее основное свойство
![]()
и
![]() (6)
(6)
Пределы интегрирования заменены на к и - к, так как ![]() при |x| > К (действительная часть комплексного числа равна 0). Для вычисления звуковой мощности находим распределение колебательной скорости, которое возбуждается линейной силой в пластине. Одномерное уравнение колебаний пластины записывается
при |x| > К (действительная часть комплексного числа равна 0). Для вычисления звуковой мощности находим распределение колебательной скорости, которое возбуждается линейной силой в пластине. Одномерное уравнение колебаний пластины записывается
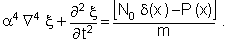 (7)
(7)
Здесь ξ- смещение; ![]() - жесткость;
- жесткость;
сп - скорость продольной волны в материале пластины;
h - толщина плиты;
n - коэффициент Пуассона;
m - масса 1 м2 плиты;
N0 - сила на единицу длины;
δ (х) - дельта-функция Дирака;
Р (х) - звуковое давление.
Дифференцируя (7) по времени, получают уравнение для скорости точек пластины
![]() (3.8)
(3.8)
где ![]() - изгибное волновое число на частоте w.
- изгибное волновое число на частоте w.
При выводе выражения (8) предполагалось, что ξ, N0, Р(х) ~ е i ω t, т.е. смещение, сила и давление - гармонические функции времени.
Дифференциальное уравнение (8) заменяется алгебраическим для спектральной амплитуды Sυ (χ), используя соотношения (1) - (4).
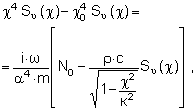
откуда следует
![]() (9)
(9)
где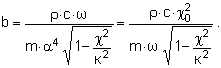
Формула звуковой мощности (5) приводится к следующему виду [4]
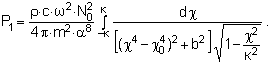 (10)
(10)
При высоких частотах ![]() >>
>> ![]() и m × ω >> r×c интеграл (10) можно вычислить и найти звуковую мощность, излученную с единицы ширины плиты [4]
и m × ω >> r×c интеграл (10) можно вычислить и найти звуковую мощность, излученную с единицы ширины плиты [4]
![]() (11)
(11)
Для учета внутреннего трения вводится коэффициент потерь h и заменяется в формуле (10) ![]() на
на ![]()
Расчет показывает, что звуковая мощность уменьшается на величину ![]() , т.е. это доля полной энергии, которая превратится в звук.
, т.е. это доля полной энергии, которая превратится в звук.
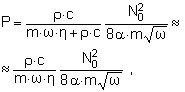 (12)
(12)
где m×ω×η - сопротивление потерь на единицу площади пластины;
ρ×с - сопротивление излучения; m×ω×η >> ρ×с.
При частотах, близких к частоте совпадения, когда к ≈ χ0, т.е. волновое число излучаемого звука примерно равно изгибному волновому числу колебания пластины на частоте w, интеграл (3.10) вычисляется иным способом [4]
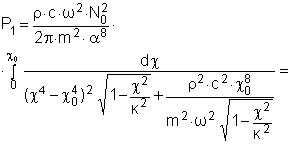
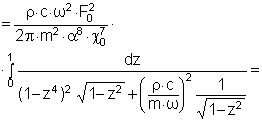
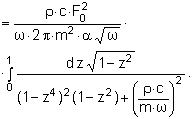
Здесь ![]()
При ρ×с << m×ω последний интеграл вычислен графически [4, рис.12, 10]; он равен примерно 0,4 для нашего случая.
Окончательно получим величину излучаемой мощности в области средних частот
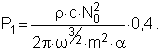 (13)
(13)
При ρ×с << m×ω из (12) и (13) следует, что частотная зависимость мощности излучения при высоких и средних частотах одинакова: с ростом частоты мощность излучения убывает по закону ω -3/2.
Лесопильная рама имеет 2 пары ползунов - верхние и нижние - и 8 направляющих. Интенсивность соударений и величины силы удара согласно [7] больше у нижних ползунов, поэтому считаем, что главные источники излучения шума - 4 направляющие нижних ползунов. Если пренебречь явлением интерференции звука, излучаемого различными источниками, результирующую мощность излучения можно вычислить, умножив выражение (12) или (13) на четыре.
Выполним расчет для серийной рамы РД75-6.
Исходные данные:
толщина направляющих h = 0,02 м; длина направляющих ζ= 0,88 м; ширина направляющих а = 0,12 м; модуль упругости материала Е = 1×1011 н/м2; плотность материала ρ = 7×103 кг/м3; жесткость плиты (расчетная схема направляющей) по формуле [4, c.274]
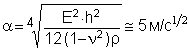 ;
;
масса 1 м2 направляющих m = 140 кг/м2; коэффициент потерь материала η = 0,03; коэффициент Пуассона n = 0,3; сопротивление излучения ρ×с = 420 кг/м2×с.
Формулу (12) преобразуем к виду, более удобному для сравнения с экспериментальными данными:
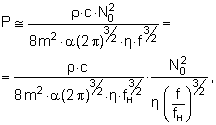
где fн = 63 Гц.
После подстановки числовых значений величин, входящих в формулу, имеем (для четырех направляющих)
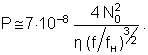 (14)
(14)
Уровень мощности в дБ
![]() (15)
(15)
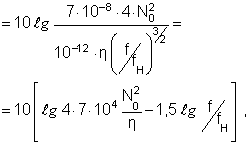
где Рпорог = 10-12 Вт/м2 - пороговое значение звуковой мощности.
Сравним эту формулу, полученную в результате расчета, с экспериментальной зависимостью (рис. 1) для 500 < f < 8000 Гц.
Спектральные уровни звуковой мощности холостого хода, полученные экспериментально и изображенные кривой 1 рисунка 1 аппроксимируем уравнением
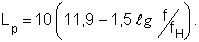 (16)
(16)
Прежде всего, отметим совпадение частотной зависимости уровня мощности, которая описывается вторыми слагаемыми в формулах (15) и (16). В обоих случаях зависимость уровня мощности от частоты описывается уравнением
![]() (17)
(17)
Сравнение слагаемых, не зависящих от частоты, в формулах (15) и (16) провести труднее, т.к. не известна величина N0 - Фурье - компонента силы удара, действующей на пластину (на единицу длины).
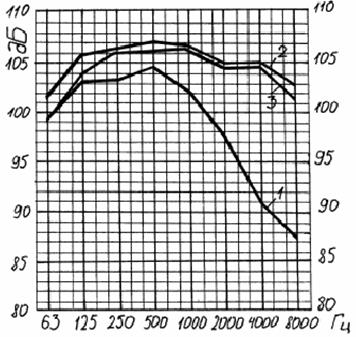
Рисунок 1. Октавные уровни звуковой мощности:
1 - при холостом ходе РД75-6; 2 - при рабочем ходе РД75-6;
3 - при рабочем ходе РД75-7
Сравнивая первые слагаемые в (15) и (16), получим
![]()
Принимая для серого чугуна η ≈ 0,03, получим оценку величины
![]()
Сила N (t), действующая на направляющую при ударе ползуна - периодическая функция времени и может быть представлена в виде ряда Фурье
![]() (18)
(18)
0 < t < T, ωn = 2π×n×fуд,
где fуд = ![]() - частота ударов (по каждой направляющей);
- частота ударов (по каждой направляющей);
n = 0, 1, 2, 3, ... - номера гармоник;
Nn - амплитуда Фурье - компоненты силы, изменяющейся с частотой ωn. Все результаты, полученные для N0, справедливы и для ![]() .
.
Из теории рядов Фурье известно, что коэффициенты Nn соответствующих гармоник должны удовлетворять неравенству 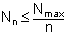 , где Nmax - максимальное значение N (t).
, где Nmax - максимальное значение N (t).
Экспериментальный график N (t) приведен в работе [7], где Nmax достигает величины порядка 6×103 кГ, а максимум силы, действующей на единицу длины линии соударения порядка 6×105 ![]() .
.
Тогда по приведенной выше оценке коэффициентов Фурье
![]()
при n = 102, N ≤ 6×103 ![]() , что согласуется с оценкой по уровню мощности (300 < 6×103)
, что согласуется с оценкой по уровню мощности (300 < 6×103)
f = n×fуд = 102×11 = 1100 Гц.
И так для любых n в пределах f = (500...8000) Гц.
При использовании направляющей с демпфирующей прокладкой, длительность удара ползуна о направляющую при перекладке возрастает. Подобная задача рассматривалась Заборовым В.И. и его сотрудниками при изучении ударного шума в зданиях [6]. Ими наблюдалось уменьшение уровня ударного шума при ударах о пол, состоящий их двух плит, разделенных упругим слоем, по сравнению с уровнем шума при ударах о сплошную плиту. Это объясняется в первую очередь увеличением длительности удара молотка установки о плиту.
Увеличением длительности импульса ударного воздействия Юдин Е.Я. и Козьяков А.Ф. [8] объясняли снижение шума при использовании валов с винтовыми ножами при фрезеровании древесины.
При использованном выше методе расчета, длительность удара τ явно не входит в формулы (12) или (13); однако можно провести качественные оценки изменения излучаемой мощности при изменении τ. При увеличении длительности удара τ, как следует из условия постоянства переданного за период импульса N(t)×τ = const убывает величина максимальной силы удара Nmax (для простоты считаем, что импульс силы имеет треугольную форму). Следовательно, коэффициенты Nn в силу неравенства ![]() должны убывать. Согласно (12) и (13) уменьшение Nn приводит к уменьшению мощности звукового излучения. Наши исследования с направляющими с демпфирующим слоем показали, что присутствие демпфирующего элемента между двумя однородными плитами позволяет уменьшить уровень излучаемой мощности плиты до (5 - 7) дБ в октавных полосах спектра (при частотах f > fH совпадения). Если принять, что N ~
должны убывать. Согласно (12) и (13) уменьшение Nn приводит к уменьшению мощности звукового излучения. Наши исследования с направляющими с демпфирующим слоем показали, что присутствие демпфирующего элемента между двумя однородными плитами позволяет уменьшить уровень излучаемой мощности плиты до (5 - 7) дБ в октавных полосах спектра (при частотах f > fH совпадения). Если принять, что N ~ ![]() , то это уменьшение уровня звуковой мощности можно объяснить увеличением длительности удара t в (1,8...2,2) раза. Эта оценка увеличения t в результате введения упругого слоя в плиту вполне реальна [9].
, то это уменьшение уровня звуковой мощности можно объяснить увеличением длительности удара t в (1,8...2,2) раза. Эта оценка увеличения t в результате введения упругого слоя в плиту вполне реальна [9].
Вышеприведенные выкладки касались октавных полос со среднегеометрической частотой выше 500 Гц, т.е. выше частоты совпадения, которая рассчитывалась следующим образом.
Скорость распространения изгибной волны в пластине зависит от круговой частоты следующим образом
![]() (19)
(19)
Частотой совпадения называется частота, при которой длина звуковой волны в воздухе λ воз. совпадает с длиной изгибной волны в пластине:
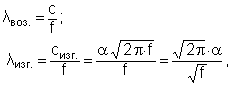
с - скорость звука в воздухе; λвоз. = λизг.;
Тогда 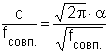 , откуда
, откуда
![]()
Для нашего случая частота совпадения для рамы РД75-6
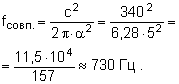 (20)
(20)
Длина изгибной волны, соответствующая этой частоте, равна 0,47 м или примерно равна половине длины направляющей ζ
![]() (21)
(21)
Частота 730 Гц близка к верхней граничной частоте октавной полосы со среднегеометрической частотой 500 Гц, равной 710 Гц.
При частотах совпадения (т.е. при f < 500 Гц), излучаемая звуковая мощность слабо зависит от частоты (см. рис. 1). Зависимость Lр от частоты в этой области аппроксимируется зависимостью
![]() (22)
(22)
На низких частотах при λ > ζ (длина звуковой волны больше размеров пластин) источник (плиту) можно считать точечным, а его мощность излучения примерно постоянна в данной области частот. Вышеприведенная теория, применимая к пластинам бесконечной длины или хотя бы к таким, размеры которых велики с длиной излучаемой волны, не применима.
СПИСОК ЛИТЕРАТУРЫ
- Черемных Н.Н. Акустическая мощность двухэтажных лесопильных рам. //Лесной журнал.-1974, №3, с. 62...65
- Черемных Н.Н. Исследование причин и закономерностей шумообразования лесопильных рам.//Труды УЛТИ, 1973, выпуск 29, с. 184...196
- Черемных Н.Н. Методика акустических расчетов лесопильном деревообрабатывающем производстве.//М.: Минлеспром СССР,- 1986,- 90 с.
- Скучик Е. Простые и сложные колебательные системы.//М.: Мир, -1971,- 557 с.
- Скучик Е. Основы акустики.//М.: ГИФМЛ, -1959,- 1182 с.
- Заборов В.И., Росин Г.С., Тюменцева Л.П. О снижении ударного шума рулонными полами. //Акустический журнал.- 1966, - Т.12, выпуск 3.- с. 301...305
- Шабалин Л.А., Санников А.А., Голованников А.А,, Зязин В.В. О нагруженности ползунов пильной рамки лесопильной рамы РД-75-6. //Деревообрабатывающая промышленность,- 1972. - № 1. - с. 11 ... 12
- Козьяков А.Ф., Юдин Е.Я. Исследования по снижению шума деревообрабатывающих станков.//Труды НИИСФа, - 1968, выпуск 5, - с. 100 ... 122
- Росин Г.С. Измерение динамических свойств акустических материалов.//М.: Стройиздат, 1972, - 175 с.
Библиографическая ссылка
Черемных Н.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВОЗНИКНОВЕНИЯ УДАРНОГО ШУМА В УЗЛАХ ПОЛЗУН – НАПРАВЛЯЮЩИЕ ЛЕСОПИЛЬНЫХ РАМ // Современные наукоемкие технологии. 2006. № 6. С. 22-27;URL: https://top-technologies.ru/ru/article/view?id=22833 (дата обращения: 24.01.2026).



