Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Бакшеев В.А Хорунжин В.С. Хомченко В.Г.

Разработана математическая модель пространственного шарнирного шестизвенника, позволяющая синтезировать механизмы с приближенным выстоем выходного звена и регулируемыми параметрами циклограммы. Приведен пример синтеза, доказывающий работоспособность предлагаемой модели. Показана возможность регулирования параметров циклограммы движения выходного звена пространственного шарнирного шестизвенника с приближенной остановкой за счет изменения длин его звеньев.

Статья в формате PDF

260 KB

Проектирование машин с переналаживаемыми параметрами на сегодняшний день является одной из актуальных задач машиностроения. Обзор механизмов с регулируемыми параметрами циклограмм и методов их синтеза показал, что такие механизмы востребованы в различных отраслях промышленности, в том числе в станкостроительной. Среди них большое распространение получили шарнирные механизмы второго класса.

Как показано в работе [1], получить движение выходного звена плоского механизма по заданной циклограмме с приближенным выстоем в крайнем положении можно с помощью двух четырехзвенников - исходного и присоединяемого, причем первый из них формирует интервалы движения и выстоя, а второй «улучшает» выстой и обеспечивает требуемый размах выходного звена. В работе [2] предложена методика синтеза пространственных рычажных механизмов с приближенными выстоями выходного звена по заданной циклограмме без регулирования ее параметров. Поставим задачу геометрического синтеза пространственного шарнирного механизма с регулируемыми параметрами циклограммы. Задачу решим в два этапа. На первом этапе разработаем математическую модель шестизвенника, а на втором рассмотрим возможность регулирования параметров циклограммы за счет изменения длин звеньев механизма.

На рис.1 изображена схема шестизвенного механизма, включающего исходный кривошипно-коромысловый четырехзвенник ABCD и присоединяемый двухкоромысловый четырехзвенник EFGH. Заданы оси вращения Z, Z₁, Z₂ кривошипа и коромысел, а также положения шарнирных точек A, D, E, H. Кроме того, заданы вспомогательные системы координат X^AY^AZ^A, X^DY^DZ^D, X^EY^EZ^E, X^HY^HZ^H с центрами в указанных шарнирных точках, причем оси X^A, X^D и оси X^E, X^H попарно лежат в одной плоскости.

Определим параметры четырехзвенника ABCD по заданным характеристикам циклограммы: углу φ₁ поворота кривошипа на первом интервале движения и углу выстоя φ_В. Зададим угол φ₀ начального положения кривошипа АВ₀. В системе координат X^AY^AZ^A уравнение плоскости, параллельной оси Z^A и содержащей прямую АВ₀, имеет вид

sinφ₀×x^A - cosφ₀×y^A = 0.

Угол асимметрии интервалов движения θ = φ₁ + φ_B /2 - π.   Этот угол, добавленный к углу φ₀, определяет положение биссектрисы B_sB_s´ угла выстоя φ_B. Запишем уравнение биссектрисной плоскости

sin(φ₀+θ) × x^A - cos(φ₀+ θ) × y^A = 0.

При переходе к системе координат X^DY^DZ^D указанные плоскости пересекаются с плоскостью X^DY^D по линиям

L₀: l₀ x^D + m₀ y^D + n₀ =0;

L₁: l₁ x^D + m₁ y^D + n₁ =0,

где

l₀ = T^DA_xx × sinφ₀ - T^DA_xy ×cosφ₀; m₀ = T^DA_yx ×sinφ₀ - T^DA_yy ×cosφ₀;

n₀ = x^A_D sinφ₀ - y^A_D cosφ₀; l₁ = T^DA_xx ×sin(φ₀+θ)- T^DA_xy ×cos(φ₀+θ);

m₁= T^DA_yx×sin(φ₀+θ) - T^DA_yy ×cos(φ₀+θ); n₁ =  x^A_D sin(φ₀+θ) - y^A_D cos(φ₀+θ).

Здесь T^DA - матрица направляющих косинусов системы X^DY^DZ^D относительно системы X^AY^AZ^A; x^A_D, y^A_D - координаты точки D в системе X^AY^AZ^A.

Зададим длину кривошипа AB = a, а значит и положения точек B₀, B₁. Тогда в системе координат X^DY^DZ^D для двух крайних на интервале движения положений коромысла CD можно составить систему уравнений:

l₀ x^D_С0 + m₀ y^D_С0 + n₀ =0;

l₁ x^D_С1 + m₁ y^D_С1 + n₁ =0;

x^D_C0²+y^D_C0² = x^D_C1²+y^D_C1²= c²;          (1)

 (x^D_C0 -x^D_B0)²+(y^D_C0 -y^D_B0)²+(z^D_B0)² =

 = (x^D_C1 -x^D_B1)²+(y^D_C1 -y^D_B1)²+(z^D_B1)² = b².   

Решение системы (1) не вызывает трудностей и позволяет найти длины b и c шатуна BC и CD соответственно, а также угол γ^m поворота коромысла CD на интервале движения (вывод опущен).

После определения наибольшего размаха γ_max коромысла CD (решение общеизвестно) можно найти перемещение коромысла CD на интервале выстоя Δγ = γ_max - γ^m .

Определим параметры присоединяемого четырехзвенника EFGH по заданному размаху ψ^m коромысла GH на интервале движения. Зададим длину коромысла GH = g, а также его угловое начальное положение ψ₀. При этом станут известны положения точек G₀, G₁ . На интервале выстоя коромысло EF, как и коромысло CD, поворачивается на угол Δγ. Учитывая, что плоскость, включающая биссектрису этого угла и точку G₁, перпендикулярна плоскости вращения коромысла EF, угол, определяющий положение указанной биссектрисы, ε_s = arccos(x^E_G1 / √ [(x^E_G1)²+(y^E_G1)²]). 

Угол начального положения коромысла EF: ε₀ = π + ε_s - Δγ/2 - γ^m. Для определения длин e и f коромысла EF и шатуна FG соответственно используем соотношения:

x^E_F0 = e×cosε₀; y^E_F0 = e×sinε₀; z^E_F0 = 0;                       (2)

x^E_F1 = e×cosε₁; y^E_F1 = e×sinε₁; z^E_F1 = 0,                       (3)

где ε₁ = ε₀ + γ^m, а также уравнения связей:

(x^E_G0 -x^E_F0)²+(y^E_G0 -y^E_F0)²+(z^E_G0)² = f²;

(x^E_G1 -x^E_F1)²+(y^E_G1 -y^E_F1)²+(z^E_G1)² = f².             (4)

Решение системы (4) с учетом соотношений (2) и (3) позволяет определить длины e, f коромысла EF и шатуна FG (вывод опущен).

Таким образом, кинематические параметры присоединяемого четырехзвенника EFGH и механизма в целом определены.

Рисунок 1. Схема шарнирного шестизвенного механизма

Угол асимметрии интервалов движения θ = φ₁ + φ_B /2 - π. Этот угол, добавленный к углу φ₀, определяет положение биссектрисы B_sB_s´ угла выстоя φ_B. Запишем уравнение биссектрисной плоскости

sin(φ₀+θ)×x^A - cos(φ₀+θ)×y^A = 0.

При переходе к системе координат X^DY^DZ^D указанные плоскости пересекаются с плоскостью X^DY^D по линиям

L₀: l₀ x^D + m₀ y^D + n₀ =0;       

L₁: l₁ x^D + m₁ y^D + n₁ =0,       

где l₀ = T^DA_xx × sinφ₀ - T^DA_xy ×cosφ₀; m₀ =

= T^DA_yx ×sinφ₀ - T^DA_yy ×cosφ₀;

 n₀ = x^A_D sinφ₀ - y^A_D cosφ₀; l₁ =

=  T^DA_xx ×sin(φ₀+θ)- T^DA_xy ×cos(φ₀+θ);

m₁= T^DA_yx×sin(φ₀+θ) - T^DA_yy ×cos(φ₀+θ); n₁ =

= x^A_D sin(φ₀+θ) - y^A_D cos(φ₀+θ).

Здесь T^DA - матрица направляющих косинусов системы X^DY^DZ^D относительно системы X^AY^AZ^A; x^A_D, y^A_D - координаты точки D в системе X^AY^AZ^A.

Зададим длину кривошипа AB = a, а значит и положения точек B₀, B₁. Тогда в системе координат X^DY^DZ^D для двух крайних на интервале движения положений коромысла CD можно составить систему уравнений:

l₀ x^D_С0 + m₀ y^D_С0 + n₀ =0;

l₁ x^D_С1 + m₁ y^D_С1 + n₁ =0;

x^D_C0²+y^D_C0² = x^D_C1²+y^D_C1²= c²;           (1)

(x^D_C0 -x^D_B0)²+(y^D_C0 -y^D_B0)²+(z^D_B0)² =

 = (x^D_C1 -x^D_B1)²+(y^D_C1 -y^D_B1)²+(z^D_B1)² = b².   

Решение системы (1) не вызывает трудностей и позволяет найти длины b и c шатуна BC и CD соответственно, а также угол g^m поворота коромысла CD на интервале движения (вывод опущен).

После определения наибольшего размаха g_max коромысла CD (решение общеизвестно) можно найти перемещение коромысла CD на интервале выстоя Δγ = γ_max - γ^m .

Определим параметры присоединяемого четырехзвенника EFGH по заданному размаху ψ^m коромысла GH на интервале движения. Зададим длину коромысла GH = g, а также его угловое начальное положение ψ₀. При этом станут известны положения точек G₀, G₁ . На интервале выстоя коромысло EF, как и коромысло CD, поворачивается на угол Δγ. Учитывая, что плоскость, включающая биссектрису этого угла и точку G₁, перпендикулярна плоскости вращения коромысла EF, угол, определяющий положение указанной биссектрисы, ε_s = arccos(x^E_G1 / √ [(x^E_G1)²+(y^E_G1)²]).

Угол начального положения коромысла EF: ε₀ = π + ε_s - Δγ/2 - γ^m. Для определения длин e и f коромысла EF и шатуна FG соответственно используем соотношения:

x^E_F0 = e × cosε₀; y^E_F0 = e × sinε₀; z^E_F0 = 0;                       (2)

x^E_F1 = e × cosε₁; y^E_F1 = e × sinε₁; z^E_F1 = 0,                       (3)

где ε₁ = ε₀ + γ^m, а также уравнения связей:

(x^E_G0 -x^E_F0)²+(y^E_G0 -y^E_F0)²+(z^E_G0)² = f²;

(x^E_G1 -x^E_F1)²+(y^E_G1 -y^E_F1)²+(z^E_G1)² = f².                       (4)

Решение системы (4) с учетом соотношений (2) и (3) позволяет определить длины e, f коромысла EF и шатуна FG (вывод опущен).

Таким образом, кинематические параметры присоединяемого четырехзвенника EFGH и механизма в целом определены.

С использованием вышеприведенных зависимостей синтезируем пространственный рычажный механизм с характеристиками циклограммы:

угол 1-го интервала движения φ₁ = 135° ; угол интервала выстоя φ_B = 120° ; угол 2-го интервала движения φ₂ = 105° ; размах выходного коромысла EH на интервале движения ψ^m = 45°.

Пусть ось вращения кривошипа совпадает с осью Z исходной системы координат с центром в точке О. Оси вращения Z₁, Z₂ имеют начальные точки O₁(100; 50; 0), O₂(100; -200; 0) и направляющие косинусы единичных векторов z₁={0,707; 0; 0,707}, z₂={ 1; 0; 0}. Расстояния, определяющие положения шарнирных точек A, D, E, H: l_OA = 200; l_O1D = 100; l_O1E = 200; l_O2H = 100. При этом размерность линейных величин - мм, угловых - град. Результаты расчета сведем в табл.1.

Таблица 1. Результаты расчета

Приращение угла поворота выходного звена на интервале выстоя Δψ = 0,32° , что составляет 0,72 % от размаха коромысла ψ^m.

Поставленная задача по разработке математической модели решена и подкреплена примером.

ЧАСТЬ 2. РЕГУЛИРОВАНИЕ ПАРАМЕТРОВ ЦИКЛОГРАММЫ

После синтеза механизма по заданной (исходной) циклограмме будем изменять характеристики последней за счет регулирования некоторых параметров механизма. В качестве регулирующих параметров могут использоваться, вообще говоря, любые кинематические параметры механизма, однозначно определяющие его схему. В данном механизме (рис.2) это длины звеньев a, b, c, e, f, g и угол ν. Кроме того, на конфигурацию механизма влияют положения шарнирных точек A, D, E, H, задаваемые расстояниями l_A, l_D, l_E, l_H от опорных точек O, O₁, O₂ соответственно, которые в некоторых случаях тоже могут быть варьируемыми.

Проведем исследование возможности регулирования параметров циклограммы на конкретном примере. Для этого рассмотрим различные варианты регулирования ее характеристик за счет параметров механизма. При этом не будем менять углы φ₀ = 35⁰, ψ₀ = 60⁰ начальных положений входного и выходного звеньев, так как в противном случае это приведет к фазовому сдвигу циклограммы, устранение которого потребует дополнительных регулировок.

Пусть исходный механизм имеет следующие параметры циклограммы (нулевой вариант данных):

φ₁ = 135° ; φ_B = 120° ; φ₂ = 105° ; ψ^m = 45°.

Для сравнительного анализа регулирующих параметров механизма по различным циклограммам результаты синтеза сведем в табл.2. Здесь же представим максимальный угол давления u_max (принятое ограничение на синтез по углу давления составляет 60⁰) и погрешность выстоя Δψ /ψ^m , выраженную в процентах.

Рассмотрим варианты регулирования параметров циклограммы.

Вариант 1. Пусть меняется только размах выходного звена ψ^m. Новые параметры циклограммы:

φ₁ = 135° ; φ_B = 120° ;

φ₂ = 105° (θ = 15°); ψ^m = 30°.

Как следует из табл.2, регулирование размаха выходного звена можно осуществить изменением только параметров e, f, определяющих конфигурацию четырехзвенника EFGH. Практически регулирование размаха выходного звена выполняется смещением общего шарнира F по линиям EF и FG при открепленном от вала DE, т.е. свободно вращающемся коромысле EF, и неподвижном выходном коромысле GH. После установки шарнира F в новое положение достаточно вновь зафиксировать коромысло EF на валу DE. При этом угол n (назовем этот параметр пассивным) автоматически примет необходимое значение. Фактически сказанное выше означает, что для регулирования размаха выходного коромысла необходимо изменить начальное положение шарнира F.

Рисунок 2. Пространственный шарнирный шестизвенник

Вариант 2. Меняется только угол интервала выстоя φ_B. Размах ψ^m и угол асимметрии интервалов движения θ постоянны. Новые параметры циклограммы: φ₁ = 150° ; φ_B = 90° ; φ₂ = 120° (θ = 15°); ψ^m = 45°.

В данном примере все параметры четырехзвенника ABCD не изменились. Это означает, что и в данном варианте регулирования циклограммы можно ограничиться изменением только параметров e, f (назовем эти параметры активными).

Вариант 3. Меняется только угол асимметрии интервалов движения θ. Размах ψ^m и угол интервала выстоя φ_B постоянны.

Новые параметры циклограммы: φ₁ = 120° ;φ_B = 120° ; φ₂ = 120° (θ = 0°); ψ^m = 45°.

Все промежуточные параметры механизма, как следует из табл.2, изменились. Это означает, что и в данном варианте регулирования циклограммы необходимо задействовать параметры обоих четырехзвенников. Практически такое регулирование выполняется смещениями начальных положений шарниров С и F (при свободно вращающемся коромысле EF).

Вариант 4. Меняется все параметры циклограммы (общий случай).

Пусть новая циклограмма имеет следующие параметры:

φ₁ = 140° ; φ_B = 100° ;

φ₂ = 120° (θ = 10°); ψ^m = 40°.

Результаты синтеза аналогичны варианту 3.

Таким образом, нетрудно сделать вывод, что и в общем случае регулирование циклограммы можно осуществить смещением начальных положений шарниров С и F. В каждом рассмотренном выше примере регулирования параметров циклограммы мы использовали исходный механизм с одинаковыми значениями параметров φ₀ , a , g , ψ₀ , которые остаются неизменными в процессе регулирования. В дальнейшем будем называть указанные параметры постоянными параметрами механизма.

Таблица 2. Сводная таблица вариантов синтеза механизма

Очевидно, что этим параметрам следует задавать такие значения, при которых, например, обеспечивались бы более благоприятные условия работоспособности путем ограничения углов давлений в шарнирах C и F, уменьшались длины звеньев и т.д.

Если заданы границы изменения параметров циклограммы, т.е. задана область параметров циклограммы, графически представляющая собой прямоугольный параллелепипед, то следует подобрать постоянные параметры так, чтобы синтезированный механизм удовлетворял условиям синтеза во всей области. Для этого необходимо выполнить синтез механизма для двух смежных вершин параллелепипеда:

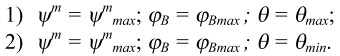
Если в данных «экстремальных» точках механизм существует и соответствует условиям синтеза, то, с большой вероятностью, он также будет удовлетворять условиям синтеза во всех остальных точках области.

Приведем пример.

Пусть для синтезированного механизма задана следующая область параметров циклограммы:

30° ≤ ψ^m ≤ 45°;

90° ≤ φ_B ≤ 120°;

0° ≤ θ ≤ 15°.

Тогда исходный вариант (вариант 0) механизма и вариант 1 соответствуют экстремальным точкам области параметров циклограммы; остальные варианты также соответствуют области параметров, о чем свидетельствуют данные, представленные в табл.2.

СПИСОК ЛИТЕРАТУРЫ

1. Хомченко В.Г. Проектирование плоских рычажных механизмов цикловых машин-автоматов и манипуляторов. - Омск: Изд-во ОмГТУ, 1995.-155с.
2. Хорунжин В.С., Хомченко В.Г., Бакшеев В.А. Проектирование пространственных рычажных механизмов цикловых машин-автоматов с остановками рабочих органов. - Кемерово: Изд-во Кемеровский технологич. ин-т пищ. пром., 2000.-188 с.

Библиографическая ссылка