Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Иванов Е.М.

Показано, что сила F, действующая на тело массы m в течение времени t, совершает работу и тогда, когда тело остается неподвижным. В общем случае работа определяется выражением: A=(F•t) ² / 2m.

Статья в формате PDF

259 KB

В школьных и вузовских курсах физики утверждается: если под действием силы изменяется абсолютное значение скорости, то говорят, что сила совершает работу [1]. Если под действием силы F материальная точка прошла бесконечно малый путь dS, то величина

                                     (1)

где α-угол между векторами F и dS, называется работой силы F на пути dS [2]. Говорят, что сила совершает работу, когда ее точка приложения перемещается [3,4]. К сожалению, в физике укоренилась неправильная трактовка понятия РАБОТЫ СИЛЫ, а именно только ее внешнее проявление: изменение скорости, перемещение тела на некоторое расстояние S и перемещение точки приложения силы. Однако следует понимать, что перемещение тела или изменение скорости - это видимый результат или следствие работы, а не сама работа. Работа совершается силой, точнее - импульсом силы .

Так, например, точка приложения силы может перемещаться без совершения работы. Поясним это на примере. Пусть деревянный брусок равномерно поднимается вверх силой тяги F_T в однородном поле силы тяжести. Поместим в брусок два электрических заряда (рис. 1 а и в). На каждый из зарядов действует кулоновская сила F_Э. Согласно вышеприведенного утверждения эти силы совершают работу. На самом же деле эти силы никакой работы не совершают (кроме работы деформации бруска). В работе подъема участвует только сила тяги F_T.

А теперь представим, что тело закреплено стопором и на него действует импульс силы . Тело, естественно, остается неподвижным. Так что, сила в этом случае не совершает работы? Пусть источником силы будет электрическая лебедка с постоянным крутящим моментом. Хотя тело и остается неподвижным, сила натяжения троса F остается постоянной, а лебедка будет также потреблять электроэнергию. Таким образом, электродвигатель лебедки совершает работу вне зависимости от того, перемещает трос тело или тело остается неподвижным, о чем могут свидетельствовать показания ваттметра или электросчетчика.

Приведем еще один пример. Ракета массы M с работающим двигателем неподвижно «зависла» над Землей. Согласно вышеприведенным формулам сила тяги двигателя F_T никакой работы не совершает, поскольку путь dS равен нулю. Однако, эту работу можно вычислить, зная скорость вытекающих газов из ракеты u. Будем считать массу ракеты постоянной (например, топливо подводится по невесомым трубопроводам извне). Совершаемая двигателем за время t работа A равна кинетической энергии газов , где Δm - масса газов, вытекающих за время t. Мощность двигателя . Импульс газовой струи  равен импульсу силы тяжести , отсюда расход топлива  и мощность двигателя . Работа, совершаемая силой тяги двигателя по удержанию ракеты в неподвижном состоянии (в состоянии левитации), будет равна 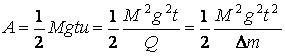, где  - секундный расход газов [кг/с].

Утверждение о том, что если тело остается неподвижным, то сила работы не производит - неверно. Вспомним определение понятия силы: сила - векторная количественная мера интенсивности взаимодействий. Проявляется в виде изменения импульса тела (количества движения mV) или деформации тел. Таким образом, даже если тело не перемещается то сила совершает работу деформации (упругой, пластической, кручения, сдвига, изгиба, среза).

Если взять пьезоэлектрический кристалл (кварц, турмалин, титанат бария, сегнетова соль) и сжать его с двух сторон, то на гранях, перпендикулярных направлению сжатия, возникают электрические заряды: на одной грани - положительные, на другой - отрицательные. Давление, деформируя кристалл, приводит к разделению центров тяжести (+) и (-) зарядов [5] и, значит, к образованию дипольного момента в каждой молекуле (если кристалл молекулярный) или в каждой группе атомов. Если поместить металлические электроды (рис. 2) и замкнуть цепь, то положительные заряды в проволоке направятся в сторону (+) зарядов кристалла и отрицательные в сторону (-) зарядов кристалла. Если прекратить сжатие, заряды потекут в обратном направлении. Осциллограф, включенный в цепь, покажет пульсирующий то в прямом, то в обратном направлении ток. На этом принципе можно превращать механическую энергию (работу) в электрическую, и наоборот, с помощью пьезоэлектрика.

Рассмотрим работу разгона по горизонтальной гладкой поверхности первоначально покоящегося тела массы  путем воздействия на него горизонтальной силой F в течение времени t. Запишем II закон Ньютона: F=ma. Умножим обе части равенства на пройденный путь S : . Поскольку , то получим  или A=K. Приведем другой вывод формулы для работы. Запишем II закон Ньютона в дифференциальной форме:

           (2)

Отметим, что правая часть уравнения может быть равна нулю, если тело остается неподвижным (V=0 ) или движется равномерно (V=const ), в то время как левая часть не равна нулю, т.е. может быть такая ситуация:

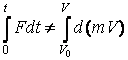             (3)

Однако вернемся к нашей задаче о разгоне неподвижного тела. После интегрирования получим: . Возведя в квадрат и разделив на 2m обе части равенства, получим:

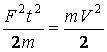 или   A=K         (4)

Таким образом, получили другое выражение для вычисления работы:

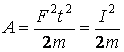                  (5)

где I = F • t - импульс силы. Это выражение не связано с путем S, пройденным телом за время t, т.е. оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным.

Рассмотрим работу той же силы, если она направлена под углом α к горизонту (рис. 3). Силу F раскладываем на две составляющие: силу тяги F_T и силу F_Л, которую назовем силой левитации, она стремится уменьшить силу тяжести. Если F_Л будет равна mg, то тело будет находиться в квазиневесомом состоянии (состоянии левитации). Используя теорему Пифагора , найдем работу силы F:

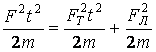 или      (6)

Поскольку F_T = ma, а S = at² / 2, то работу силы тяги можно представить в общепринятом виде . Суммарная работа, выполняемая силой F, остается той же самой, что и в первом случае (при ): .

Если на тело действует только одна сила левитации , то тело будет оставаться неподвижным на любой высоте. На это затрачивается работа левитации . Используя это выражение, можно определить работу и других сил в статическом состоянии.

Работу силы, удерживающей пружину в растянутом или сжатом состоянии, можно определить аналогично, заменив силу упругости эквивалентной силой тяжести  (рис. 4):

                (7)

В опытах Р.Милликена распыленные капельки масла вдувались в электрическое поле плоского конденсатора. Наэлектризованные капельки находились под действием двух сил: силы тяжести mg и кулоновской силы , где q - заряд капельки, m - её масса, E - напряженность электрического поля. Если капелька зависает, то условия левитации создаются двумя равными, но противоположно направленными силами . Тогда работа кулоновской силы определится из условия левитации:

                   (8).

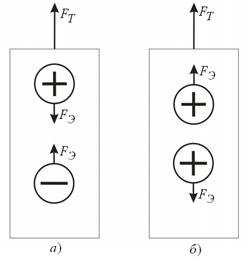
Рисунок 1. Два электрических заряда

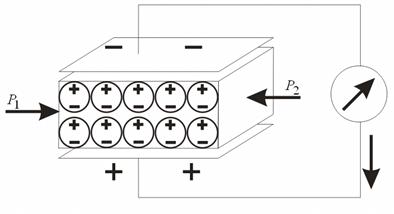
Рисунок 2. Металлические электроды

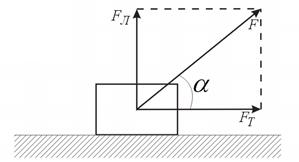
Рисунок 3. Работа силы, если она направлена под углом  к горизонту

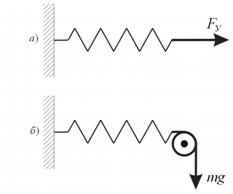
Рисунок 4. Замена силы упругости эквивалентной силой тяжести

СПИСОК ЛИТЕРАТУРЫ

1. Матвеев А.Н. Механика и теория относительности: Учеб. Пособие для физ. спец. вузов. - М.: Высш. шк., 1986.
2. Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. Механика и молекулярная физика. - М.: Наука, 1965.
3. Хвольсон О.Д. Курс физики. Том I. РСФСР Госуд.изд-во, Берлин, 1923.
4. Элементарный учебник физики. Том I. Под ред. акад. Г.С.Ландсберга. - М.: Наука, 1972.
5. Ормонт Б.Ф. Введение в физическую химию и кристаллохимию полупроводников. М.: Высш. шк., 1973. 

Библиографическая ссылка