Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Лисов А.А. Домницкий А.В. Домницкий М.В.

Современное развитие информационных технологий и вычислительной техники позволяет эффективно реализовать системный анализ и математическое моделирование при описании трехмерной реконструкции сложных биосистем. В своей работе мы ограничились детальным исследованием полости левого желудочка сердца с аномально расположенными хордами, поскольку известно, что поперечные и диагональные топографические варианты хорд приводят к деформации его полости и нарушению его функции. Ремоделирование сердечно-сосудистой системы является осложнением ряда заболеваний сердца и одновременно фактором его прогрессирования. Целью настоящего исследования явилась разработка математической модели формы левого желудочка сердца с аномально расположенными хордами на базе его трехмерной реконструкции, обеспечивающей проведение ранней диагностики сердечно-сосудистых заболеваний. Но наиболее близким к решению данных задач оказался метод свободной деформации формы. Техника свободной деформации формы состоит во вложении простой пространственной фигуры в область, содержащую исходный объект, и ее деформации до формы исходного объекта. В качестве базовой фигуры использовался суперквадрик. Совмещение осуществлялось путем минимизации ошибки совпадения по критерию среднеквадратического отклонения. Разработана модель трехмерной реконструкции формы левого желудочка сердца, заданная в виде параметрических поверхностей с деформациями, при различных топографических вариантах аномально расположенных хорд в условиях не фиксированного количества исходных данных. Показано что, при описании высокоуровневых деформаций с использованием техники свободной деформации формы, достигается гладкость поверхности и минимальное число данных для описания модели.

Статья в формате PDF

139 KB

В своей работе мы ограничились детальным исследованием полости левого желудочка сердца с аномально расположенными хордами (АРХ), поскольку известно, что поперечные и диагональные топографические варианты АРХ приводят к деформации его полости и нарушению его функции (3, 4). Ремоделирование сердечно-сосудистой системы является осложнением ряда заболеваний сердца и одновременно фактором его прогрессирования.

Современное развитие программных и аппаратных средств вычислительной техники позволяет внедрять методы моделирования и трехмерной реконструкции сложных пространственных объектов при их визуализации. Использование модели дает возможность врачу изучения признаков объекта присущих его реальному прототипу (5).

Для моделирования трехмерной формы объектов используются методы, на основе комбинации простейших геометрических объектов, связи которых заданы аналитически, таблично или графически, и методы, основанные на преобразовании и комбинации аналитически заданных поверхностей. Выбор метода моделирования во многом определяется видом технического средства и объемом полученной информации об объекте при его визуализации (6, 7).

Важным этапом в развитии методов трехмерной реконструкции формы желудочков сердца является разработка математической модели геометрии желудочков сердца с учетом особенностей их структурно-морфологического строения (8). Изучение ремоделирования сердца с АРХ левого желудочка, основанного на использовании минимального числа эхокардиографических проекций является своевременным и актуальным, а внедрение ее результатов способствует продвижению новых методов математического моделирования в клиническую практику. Результаты наших исследований повысят качество диагностики патологии сердца и обеспечат более строгий выбор тактики ведения больного.

Целью исследования - является разработка математической модели формы левого желудочка сердца c аномально расположенными хордами на базе его трехмерной реконструкции, обеспечивающей проведение ранней диагностики сердечно-сосудистых заболеваний.

Материалы и методы исследования

В качестве объекта исследования выбрано сердце с АРХ, представляющее собой орган циклически меняющий свою геометрию с внутренним побуждением к изменению систолического и диастолического контура. Данный объект обладает индивидуальными особенностями, основной задачей которого является глобальная функция. В работе использовались ультразвуковые системы «Sonos 5500», «Sonos 2500» на которых 130 больным с АРХ проведено ультразвуковое исследование сердца.

Математическая модель любого объекта в трехмерном пространстве может быть описана параметрической функцией вида (9).

где и = (θ,φ) - координаты точки в полярном пространстве Ω.

В качестве исходного примитива для реконструкции трехмерной формы объектиа использовалась суперквадратическая функция.

Результаты исследования

Математическая модель сложного биобъекта должна функционально описывать его пространственную форму и однозначно определять в любой точке его поверхности. При проектировании модели требуется братьв расчет количество исходных данных, которое может меняться в зависимости от условий ультразвуковой визуализации. Однако математическая модель обычно имеет фиксированное количество характеристик, которые не подвержены изменению.

Учитывая тот факт, что желудочек сердца с АРХ представляет собой динамический объект, меняющий форму во времени, получим

где t - момент времени, в который была произведена фиксация объекта.

С математической точки зрения функция желудочка является периодической сменой его отдельных состояний X₁(u,t), X₂(u,t)... в момент времени t=[t_s,t_d] от систолической (s) фазы к диастолической (d) (10).

Рассмотрим модель сердца с АРХ как фиксацию его состояния (геометрии) в момент времени t. Таким образом, математическая модель учитывая характер и динамику изменения формы желудочка, можно представить в виде полого цилиндра, подвергающегося геометрическим деформациям. Переход из одного состояния в другое связан с изменением закона деформирующих процессов. Следовательно математическую модель желудочка сердца можно представить параметрической функцией с введенными деформациями в виде вектора деформации:

где Х₀(u) - форма исходного примитива,

D_d(u) - функция d- деформации.

В качестве исходного примитива выберем суперквадрик. Для цилиндрического варианта уравнение с учетом u=(θ,k) может быть переписано как:

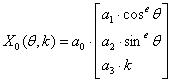
где 0 ≤k < R - параметр оси Z, а₀ - глобальный масштаб объекта; а₁, а₂, а₃- масштабные коэффициенты по осям X, Y и Z.

На практике применяется запись выражения в следующей форме:

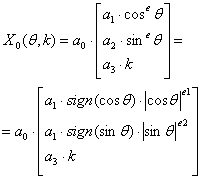
Представим масштабные коэффициенты а₁, а₂, а₃ как деформационные воздействия, направленные на изменение размера сечений относительно друг друга. Учитывая, что на каждое сечение объекта, в зависимости от топографического варианта АРХ приводящих к ремоделированию сердца могут действовать различные по величины деформации, получим:

Масштабные коэффициенты являются деформирующими функциями, действующими на примитив в плоскости х0у и изменяющие размер сечения. Сопоставив действие масштабных коэффициентов, действующих в плоскости х0у, с моделью каркаса их можно представить как функцию коэффициентов подобия S_k. Тогда a₁(k)=a₂(k)=S(k) и следовательно,

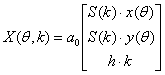
Рассмотрим другие деформации формы исходного примитива с АРХ. Каждое k-е сечение объекта с АРХ приводящими к деформации полости может быть сдвинуто относительно предыдущего на некоторую величину w в плоскости х0у. Определим такую деформацию как функцию сдвига W(k). Тогда модель желудочка запишется так:

В параметрическом виде выражение запишется так

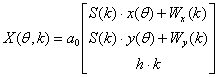
Кроме линейного масштабирования и сдвигов в плоскости х, у существует деформирующий процесс, связанный с кручением сечений вокруг условного центра относительно друг друга. Определим деформацию за счет натяжения АРХ как функцию U(k). С учетом такого воздействия математическая модель желудочков сердца запишется так:

В параметрическом виде выражение (2.13) запишется как:

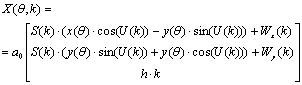
Исходными данными для функций деформации S(k),W_x(k),W_y(k) и U(k) является соответствующие векторы значений:

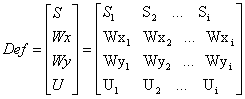
где i = 0,1...N текущее сечение.

Переход от вектора к непрерывной функции одного аргумента k осуществляется путем интерполяции по точкам вектора Def. Для достижения плавности переходов применены сплайны (11).

Деформирующие воздействия Def можно считать низкоуровневыми и грубыми, поскольку они позволяют лишь частично корректировать форму. В данном случае выражение описывает поведение модели при изменении конфигурации сечения только по длинной оси. Воздействия Def геометрически идентичны реальным физическим процессам искривления, воздействующим на форму желудочка в данной проекции.

Однако полученная модель не может быть вписана в каркас, поскольку в ней отсутствуют деформации, придающие ей форму, отличную от эллиптической. Такая информация заложена в опорном контуре каркасной модели, получаемом из сечения по короткой оси. Как было показано возможности суперквадриков не обеспечивают достаточную вариабельность формы, необходимую для воспроизведения геометрических свойств правого желудочка. В данном случае для получения требуемой формы целесообразно применить технику свободной деформации, адаптировав ее для данного случая. При этом такая деформация может считаться высокоуровневой, поскольку обеспечивает необходимую вариабельность формы.

Согласно стратегии, описанной в п.1.1, определим: деформирующую сетку (m+1)(n+1)(l+1) в виде вектора узловых точек Р:

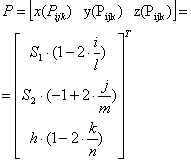
где m+1, l+1, n+1 - размерность деформирующей сетки по X,Y и соответственно; 0<i<m, 0 <j < l, 0 < k < n - текущий номер узловой точки. В практике, для моделирования желудочков сердца методом свободных деформаций используется сетка 5x5x5 (12). Этой размерности в большинстве случаев достаточно, для достижения погрешности совпадения менее 1 %. При этом, смещение узловых точек имеет 3 степени свободы.

Определим новую систему координат, образованную деформирующей сеткой, для пересчета координат исходной формы Х(θ, k) в ортогональную систему координат, где каждая точка каркаса и деформируемой формы будет иметь координаты (s, v, u), в диапазоне [0,1], причем:

Представим исходную форму в декартовой системе координат X(s,t,u) деформирующей сетки Р. Запишем ее в виде матрицы:

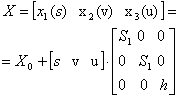
где Х₀ = [s₀, t₀, m₀] - точка начала координат (угловая точка сетки Р).

Аналогично пересчитываются точки каркаса для базового сечения. Подставив координаты X(s,v,u) в уравнение свяжем контрольные точки Р с математической моделью Н, через деформацию В, тогда можно записать:

H = B ^. P

где В - матрица деформаций, В = NH x NP, причем NH - число точек,описывающих поверхность модели Н, NP - число опорных точек; Н - вектор модели, H = NHx3,NH = (s+l)(t+l)(u+l); Р - узловые точки, P = NPx3,NP = (n+1)(m+1)(l+1). Таким образом, математическую модель желудочка можно представить системой линейных алгебраических уравнений, описывающих процесс высокоуровневых деформаций исходной формы х(θ, k).

В полученной модели на базе параметрических поверхностей с введенными деформациями, воспроизводится трехмерная геометрия модели в условиях, когда информация об объекте ограничена двумя ортогональными сечениями.

Таким образом, при описании высокоуровневых деформаций с использованием техники свободной деформации формы, достигается гладкость поверхности при минимальном числе исходных данных для описания ее математической модели.

Выводы

1. Разработана модель трехмерной реконструкции формы левого желудочка сердца, заданная в виде параметрических поверхностей с деформациями, при различных топографических вариантах аномально расположенных хорд в условиях не фиксированного количества исходных данных.
2. Показано что, при описании высокоуровневых деформаций с использованием техники свободной деформации формы, достигается гладкость поверхности и минимальное число данных для описания модели.

СПИСОК ЛИТЕРАТУРЫ

1. Иванов В.П., Батраков В.С. Трехмерная компьютерная графика. М.:Радио и связь. - 1995. - 224с.
2. Гаврилов А.В. и др. Автоматизированная компьютерная система для трехмерной визуализации ультразвуковых изображений в медицине: основные характеристики и перспективы клинического применения //Ультразвуковая диагностика. - 1996. - №1. - С.6-14.
3. Желев В., Карнолски Т. Аномально расположенные хорды сердца у членов одной семьи //Кардиология. - 1991. - N1. - С.105-106.
4. Земцовский Э.В. Соединительнотканные дисплазии сердца. Санкт - Петербург. «Политекс» -1998. - 94С.
5. Самарский А.А., Михайлов А.П. Математическое моделирование. - М. - Физматлит. - 2002. - 316с.
6. Иванов В.П., Батраков А.С. Трехмерная компьютерная графика. М.: Радио и связь, 1995.224с.
7. Timothy С. Ultrasonic Three-Dimensional Reconstruction: In Vitro and In VivoVolume and Area Measurement. 1994. 729 p.
8. Eric Bardinet, Laurent D. Cohen, Nicholas Ayache. Analyzing the deformation of the left ventricle of the heart with a parametric deformable model. Programme 4 - Robotique, image et vision //Rapport de recherché. 1996. V.797. p. 45-49.
9. Jinah Park, Dimitri Metaxas, Alistair A. Young, Leon Axel. Deformable Models with Parameter Functions for Cardiac Motion Analysis from Tagged MRI Data IEEE Transactions On Medical Imaging, V. 15. № 3. 1996. p. 121-124.
10. Алпатов А.В. Математическая модель сердца //Сборник трудов кафедры микроэлектронники. Рязань. РГРТА. - 1999. - С. 36-38.
11. Alejandro F. Frangi, Wiro J. Niessen, Max A. Viergever. Three-Dimensional Modeling for Functional Analysis of Cardiac Images. IEEE Transactions On Medical Imaging. 2001. V. 20. № 1. p. 79-83.
12. Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория конструирования систем управления. - М.: Высшая школа. - 1989. - 128с.

Библиографическая ссылка