При нестационарном криволинейном движении лесовозного автопоезда (ЛАП) возникают дополнительные (по сравнению с прямолинейным движением) силы внешнего и внутреннего взаимодействия. Выражения геометрических и кинематических параметров [1, 2] позволяют сделать их количественно-качественную оценку при любом законе движения.
Лесовозный автопоезд представляет собой сложную сочлененную механическую систему, основными элементами которой являются автомобиль-тягач, роспуск и пакет хлыстов (рис. 1).
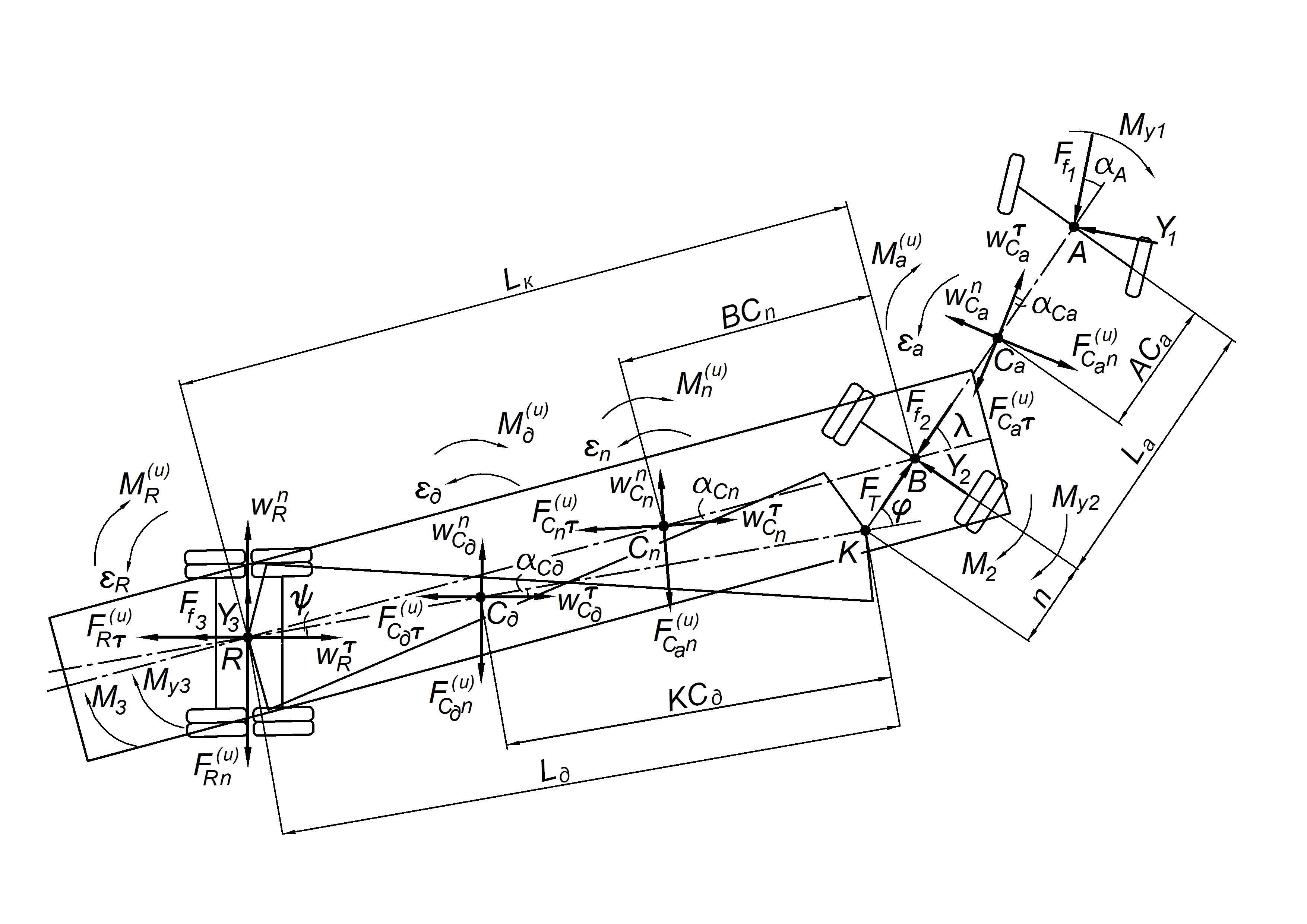
Рисунок 1. Расчетная схема. Лесовозный автопоезд на кривой
При разработке замкнутой математической модели рассматриваем состояние динамического равновесия каждого элемента в отдельности.
С учетом принятых допущений [1] уравнения имеют вид.
Автомобиль-тягач (рис. 2)
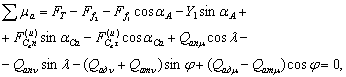
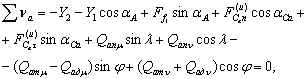
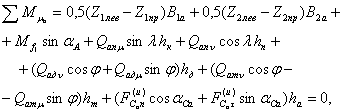
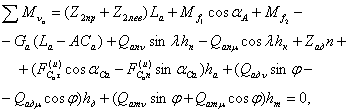
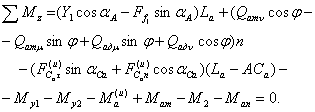
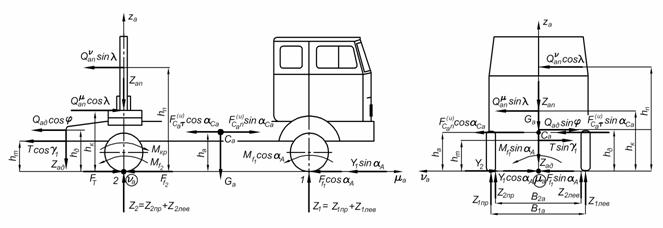
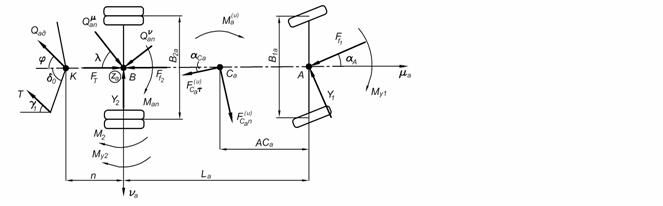
Рисунок 2. Автомобиль-тягач
Роспуск с дышлом (рис. 3)
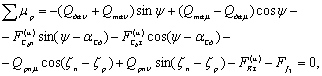
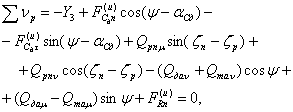
![]() (2)
(2)
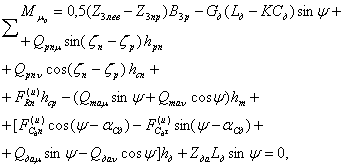
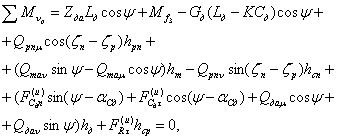
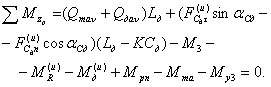
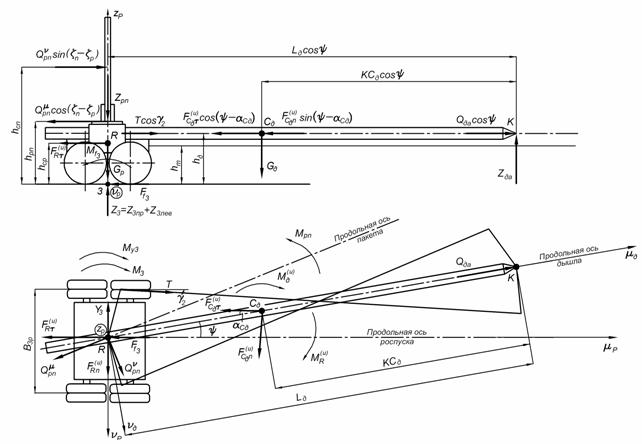
Рисунок 3. Роспуск с дышлом
Пакет хлыстов (рис. 4)
![]() ,
,
![]() ,
,
![]() , (3)
, (3)
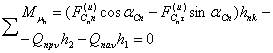 ,
,
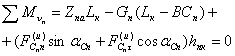 ,
,
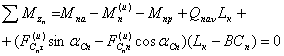 .
.
Обозначения.
FT - сила тяги, приложена к средней точке В задней оси автомобиля.
Ff1, Ff2, Ff3 - силы трения, приложенные (условно) в средних точках осей автомобиля и площадки роспуска,
Ff1=fZ1,Ff2=fZ2 ,Ff3=fZ3 ,
где Z1,Z2,Z3 - вертикальные реакции.
Mf1,Mf2 ,Mf3 - моменты сопротивления качению соответствующих осей автопоезда
Mf1=fkZ1,Mf2=fkZ2 ,Mf3=fkZ3 .
M2 и M3 - суммарные моменты сопротивления повороту спаренных колес автомобиля и роспуска (зависят от радиуса кривизны траектории средней точки оси, ширины колеи, динамического радиуса качения колес)
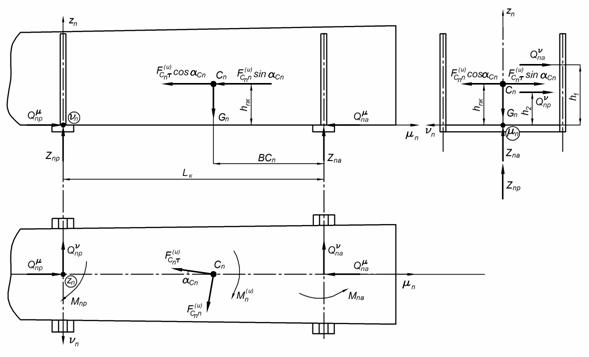
Рисунок 4. Пакет хлыстов
![]() ,
,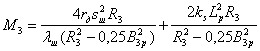 ,
,
где sш - расстояние между серединами опорных поверхностей спаренных шин, λш - коэффициент тангенциальной эластичности шины, ks - боковая жесткость шины.
My1,My2 ,My3 - моменты, возникающие из-за неравенства продольных реакций внешнего и внутреннего колес оси и направленные противоположно повороту оси.
Y1,Y2 ,Y3 - суммарные боковые реакции, условно приложенные в средних точках осей перпендикулярно к плоскости вращения колес.
Инерционные силовые факторы.
Нормальная и касательная силы инерции i-того элемента, приложенные в его центре масс,
![]() ,
,![]() .
.
Момент пары сил инерции (относительно центральной оси)
![]() ,
,
где Ji - момент инерции i-того элемента автопоезда.
Определение реакций дорожного полотна и сил внутреннего взаимодействия элементов автопоезда достигается совместным решением систем уравнений (1)-(3).
Разработанная математическая модель и ее реализация с помощью ПЭВМ позволяют провести анализ динамических параметров ЛАП для общего случая его нестационарного движения на кривых.
СПИСОК ЛИТЕРАТУРЫ
- Соколов Г.М. Движение лесовозного автопоезда на кривых. Теория. Расчет. Эксперимент / Г.М. Соколов. - ВИНИТИ, 1998. № 2507-В98. - 274 с.
- Соколов, Г. М. Геометрические характеристики движения лесовозного автопоезда на переходных кривых /Г.М. Соколов, С.А. Стариков //XI международная научно - техническая конференция по транспортной технике и технологии «trans&MOTAUTO´04». - Пловдив, Болгария, 2004. - С. 93-96.
Работа представлена на научную конференцию с международным участием «Современные наукоемкие технологии», Доминиканская республика, 5-16 апреля 2006г. Поступила в редакцию 14.03.2006г.
Библиографическая ссылка
Соколов Г.М., Стариков С.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ НЕСТАЦИОНАРНОГО ДВИЖЕНИЯ ЛЕСОВОЗНОГО АВТОПОЕЗДА НА КРИВЫХ // Современные наукоемкие технологии. 2006. № 4. С. 79-82;URL: https://top-technologies.ru/ru/article/view?id=22652 (дата обращения: 14.03.2026).



