Проведенные исследования показали, что наличие двух контрольных оснований, удовлетворяющих
![]() , (1)
, (1)
позволяет однозначно исправить однократную ошибку по любому основанию ПСКВ.
Исходя из условия, что техническое выполнение процедур поиска и коррекции ошибок в модулярном коде тесно связано с устойчивостью функционирования СП класса вычетов, очевидно, что устройство определения и локализация ошибки, состоящее из меньшего количества комплектующих элементов, оказывает меньшее воздействие на снижение надежности функционирования СП СПКВ. Данное положение полностью согласуется с экспоненциальной моделью надежности, в которой интенсивность отказов вычислительного устройства пропорционально суммарному числу элементов, из которых оно состоит [2].
Тогда математическая установка задачи выбора нейросетевой реализации процедуры поиска и коррекции ошибок в модулярном коде имеет вид
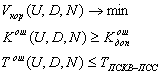 ,
,
где Vкор - схемные затраты; U - алгоритм обнаружения и коррекции ошибок в модулярных кодах; D - пространственно-временное распределение алгоритма в нейросетевом базисе; N - набор модулей полиномиальной системы классов вычетов;K ош - количество парируемых ошибок выбранным алгоритмом;К ошдоп - минимально допустимое количество обнаруженных и исправленных ошибок; Тош - временные затраты необходимые на реализацию процедуры поиска и коррекции ошибки; Тпскв-псс - временные затраты на обратное преобразование из модулярного кода в позиционный код.
В таблице 1 представлены исходные данные, необходимые для решения поставленной задачи для ПС ПСКВ, функционирующих в GF(23), GF(24), GF(25).
Таблица 1. Исходные данные для выбора алгоритма коррекции ошибок
|
№ п/п |
Алгоритм поиска и исправления ошибок |
Кратность ошибки |
Затраты на реализацию алгоритма |
|||
|
аппаратурные (нейроны) |
временные (кол-во итераций |
|||||
|
GF(23) |
GF(24) |
GF(25) |
||||
|
1 |
Параллельная нулевизация |
1 |
15 |
40 |
85 |
1 |
|
2 |
Интервальный номер |
1 |
14 |
42 |
109 |
1 |
|
3 |
Коэффициенты ОПС |
1 |
14 |
67 |
197 |
1 |
|
4 |
Синдром ошибки |
1 |
18 |
41 |
87 |
1 |
Анализ таблицы 1 показывает, что оптимальным способом реализации немодульной процедуры определения, локализации и исправления ошибки для конвейерной структуры СП ПСКВ с двумя контрольными основаниями является алгоритм определения нормированного следа полинома. Данный алгоритм реализуется на основе двухслойной нейронной сети прямого распространения, требуя при этом минимальных аппаратурных и временных затрат.
Однако, если учитывать то обстоятельство, что коэффициенты ОПС используется при выполнении процедур перевода непозиционного кода ПСКВ в позиционную систему счисления, то при проведении сравнительного анализа необходимо учитывать и схемные затраты необходимые для обратного преобразования на основе КТО. Тогда получаем, что для реализации процедуры поиска и локализации ошибки при переводе кода ПСКВ в ПСС на основе позиционной характеристики - нормированный след полинома потребуется:
- для поля GF(23) - 49 нейронов;
- для поля GF(24) - 137 нейронов;
- для поля GF(25) - 400 нейронов.
Результаты решения задачи выбора алгоритма поиска, локализации и исправления ошибки для СП ПСКВ приведены в таблице 2.
Таблица 2. Результаты решения задачи выбора алгоритма поиска, локализации и исправления ошибки для СП ПСКВ
|
№ п/п |
Разрядность СП ПСКВ, бит |
Алгоритм реализации процедур |
|
1 |
7 |
коэффициенты ОПС |
|
2 |
15 |
коэффициенты ОПС |
|
3 |
31 |
коэффициенты ОПС |
Анализ таблицы показывает, что для СП класса вычетов с двумя контрольными основаниями алгоритм вычисления коэффициентов обобщенной полиадической системы является оптимальным [3]. При этом при дальнейшем увеличении разрядной сетки СП ПСКВ с параллельно-конвейерной организацией вычислений эффективность применения данного алгоритма возрастает.
Таким образом, благодаря отмеченному обстоятельству, применение нейросетевых устройств для локализации и коррекции ошибок, базирующихся на вычислении коэффициентов смешанной системы, является наиболее целесообразным.
СПИСОК ЛИТЕРАТУРЫ
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков, В.А. Галкина, Ю.О. Щелкунова, А.А Шилов; Под редакцией Н.И. Червякова.-М.: ФИЗМАТЛИТ,2003.-216с.
- Долгов А.М. Диагностика устройств, функционирующих в системе остаточных классов.-М.:Радио и связь,1982.-64с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов/Нейрокомпьютеры: разработка и применение. №12, 2004, с.51-60.
Библиографическая ссылка
Резеньков Д.Н. СРАВНИТЕЛЬНАЯ ОЦЕНКА ОСНОВНЫХ МЕТОДОВ КОНТРОЛЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ // Современные наукоемкие технологии. 2006. № 4. С. 68-69;URL: https://top-technologies.ru/ru/article/view?id=22649 (дата обращения: 14.03.2026).



