Решение проблемы: Качественно новые требования к цифровой обработке сигналов обусловили повышенный интерес к разработке математических моделей ЦОС, построенных на основе алгебраических систем, обладающим свойством конечного кольца или поля. Особое место среди таких систем занимает полиномиальная система классов вычетов (ПСКВ) [1,2,3]. Данная система относится к параллельным вычислительным системам, в которой исходный полином A(z) представляется в виде n-разрядного вектора вида
, (1)
где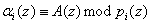 
, 
.
Наряду с высоким быстродействием, обусловленным малоразрядностью остатков и модульностью вычислений, полиномиальная система классов вычетов обладает способностью обеспечивать устойчивость к отказам вычислительным системам, функционирующим в ПСКВ. Рассматривая алгоритмы расширения системы оснований, положенные в основу метода контроля и коррекции ошибок в кодах ПСКВ с использованием синдрома ошибки, нельзя не отметить возможность применения псевдоортогональных полиномов [1].
Нарушение ортогональности по контрольным основаниям приводит к тому, что данные полиномы лежат внутри рабочего основания. Если представить полином А(z) в виде суммы ортогональных полиномов Ai(z), у которых все остатки равны нулю за исключением рi(z), т.е.
,
то справедливо
. (2)
Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безызбыточной системы оснований полиномиальной системы классов вычетов 
[1]. Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z), ..., pk(z) на r контрольных оснований pk+1(z), ..., pk+r(z) и представим ортогональные полиномы в виде
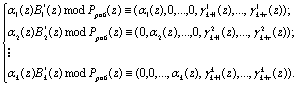(3)
Учитывая, что в процессе выполнения операции не бывает выход за пределы Pраб(z), получаем, что значение полинома
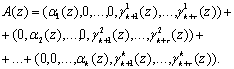
Следовательно, справедливо
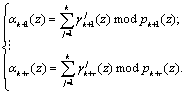(4)
Таким образом, на основании выражения (4) и воспользовавшись значениями псевдоортогональных полиномов, определяемых (3), можно вычислить значения остатков по контрольным основаниям 
согласно
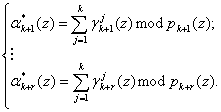(5)
Затем на основании полученных значений и значений 
, поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражения
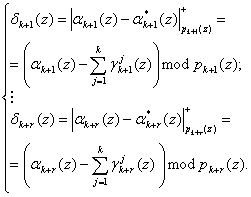(6)
Если синдром ошибки равен нулю, т.е.
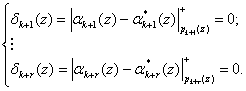. (7)
то исходный полином 
. В противном случае при условии
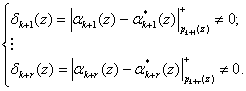, (8)
модулярная комбинация является запрещенной. Тогда в зависимости от величины синдрома ошибки осуществляется коррекция ошибки, т.е.
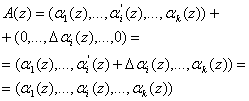(9)
где 
- вектор ошибки модулярного кода; 
- глубина ошибки по i-му модулю; 
.
В работе [1] представлена структура устройства для коррекции ошибок в полиномиальной системе классов вычетов поля GF(24) с использованием псевдоортогональных полиномов.
Выводы: Полученные данные свидетельствуют, что применение разработанного метода позволяет сократить аппаратурные затраты необходимые на реализации процедур поиска и локализации в модулярных кодах по сравнению с ранее известными методами, приведенными в работе [5], что обеспечивает более надежную работу всего вычислительного устройства ЦОС. Кроме того, для реализации процедуры вычисления синдрома ошибки требуется двухслойная НС, что позволяет выполнить операцию поиска и локализации ошибок всего за одну итерацию.
СПИСОК ЛИТЕРАТУРЫ
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа /Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68с.
- Элементы применения компьютерной математики и нейроинформатики /Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.
Библиографическая ссылка
Калмыков И.А., Хайватов А.Б., Сагдеев А.К. ОБНАРУЖЕНИЕ И КОРРЕКЦИЯ ОШИБОК В МОДУЛЯРНОМ КОДЕ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ // Современные наукоемкие технологии. – 2006. – № 4. – С. 51-53;URL: https://top-technologies.ru/ru/article/view?id=22638 (дата обращения: 19.04.2024).