Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Курамшина А.Е. Цеплин Е.Е. Бочкор С.А. Хвостенко О.Г. Кузнецов В.В.

Статья в формате PDF

226 KB

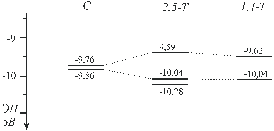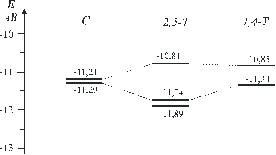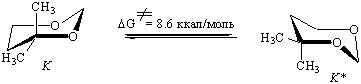
Нами с помощью квантово-химических методов в рамках пакета HyperChem 5.02 [2] исследована поверхность потенциальной энергии (ППЭ) молекул этого соединения. Расчеты подтверждают данные ЯМР. Показано, что конформационная изомеризация включает несколько равновесных процессов, представленных на схеме, которые содержат 1,4- и 2,5-T формы, соответствующие локальным минимумам на ППЭ. Максимумы (переходные состояния, ПС) отвечают 4 конформациям по данным 6-31G** и двум - согласно AM1. В рамках последнего метода пути конформационной изомеризации (1) и (2) характеризуются близкими значениями ΔЕ^≠ но различными величинами ΔЕ для 2,5-T и 1,4-T форм. Ab initio подход демонстрирует одинаковые ΔЕ для твист-конформеров, но различные ΔЕ^≠ для двух отмеченных маршрутов (табл. 1). В соответствие с этим маршрут, предполагающий образование 1,4-Т-формы несколько более предпочтителен.

Возможные пути интерконверсии К ↔ К* 4,4-диметил-1,3-диоксана

Таблица 1. Относительные энергии инверсии К ↔ К* (ΔЕ and ΔЕ^≠, ккал/моль)

С другой стороны теоретические барьеры псевдовращения относительно невелики, что делает возможным реализацию обоих маршрутов интерконверсии. Это подтверждается хорошим соответствием экспериментального (ΔG^≠) и расчетного (ΔЕ^≠ для ПС-2, ab initio) значениями соответствующего максимума на ППЭ (8.6 и 8.3 ккал/моль соответственно).

Представлялось логичным проверить результаты расчетов с помощью корректного экспериментального подхода. В качестве такового был выбран метод фотоэлектронной спектроскопии, позволяющий исследовать поведение молекулы вещества в разряженной газовой фазе, то есть в условиях, для которых и проводился квантово-химический расчет. Обзорный фотоэлектронный спектр (ФЭС) исследуемого соединения (рис. 1) получен в широком интервале энергий ионизации от 8 эВ до 16 эВ, на модернизированном ФЭ спектрометре ЭС 3201.

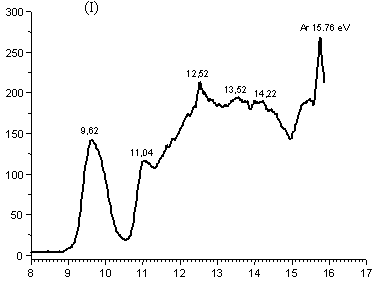
Рисунок 1. Фотоэлектронный спектр 4,4-диметил-1,3-диоксана

Он содержит первую полосу с двумя близко расположенными максимумами, соответствующими отрыву электрона высшей занятой молекулярной орбитали (ВЗМО) - связывающей -и второй занятой молекулярной орбитали (ЗМО) - разрыхляющей комбинации двух неподеленных электронных пар атомов кислорода (n_o). При этом рассматриваемая полоса имеет сложную форму, которая обусловлена наложением колебательной структуры полос двух ЗМО и определенной ассиметрией, выражающейся в наличии "плеч" на ее низко- и высокоэнергетичном склонах. Последнее служит первым экспериментальным подтверждением расчетных результатов, полученным на основе ФЭС, поскольку указывает на присутствие у молекулы неэквивалентных конформеров, характеризующихся разными значениями энергий ионизации двух высших ЗМО. Вторым экспериментальным подтверждением служит изученная нами зависимость этих спектров от температуры исследуемого образца (30 и 150 ⁰С): при повышении температуры наблюдается рост относительной интенсивности второстепенных пиков кривой фотоионизации, образующих «плечи» на склонах полос [3].

Из теории известно, что молекула, имеющая два конформационных минимума на ППЭ, Е₁ и Е₂, разделенных небольшим барьером, инвертирует между двумя состояниями, находясь с большей вероятностью в конформации с меньшей энергией (Е₁ < Е₂). И тогда соотношение вероятностей пребывания ее в двух конформациях составит величину К₂/K₁ = е ^{- ΔЕ/kT}, где ΔЕ = Е₂ - Е₁. Отсюда видно, что при любой температуре соотношение К₂/K₁ < 1, а при Т →∞ величина К₂/K₁ стремится к 1. Это означает, что при повышении температуры вещества (увеличение энергии колебательного возбуждения молекулы), должен наблюдаться рост спектральных пиков, соответствующих менее выгодным конформерам, то есть, тех пиков, которые составляют "плечи" на спектральных полосах. Именно такая картина была обнаружена нами для исследованного 1,3-диоксана (рис. 2).

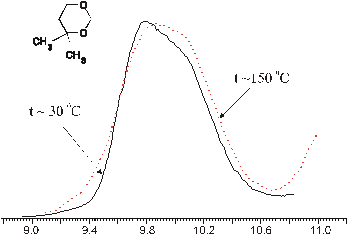
Рисунок 2. Влияние температуры на вид первой полосы фотоэлектронного спектра 4,4-диметил-1,3-диоксана

Полоса в области 9-11 эВ из ФЭС ДМД соответствует двум высшим занятым МО, соответствующим неподеленным парам электронов атомов кислорода, а сама молекула, согласно результатам описанных выше квантово-химических расчетов, имеет три конформационных минимума. Отсюда следует, что указанная полоса является, во-первых, суммарной и, во-вторых, должна состоять, по меньшей мере из шести пиков. Последние должны при этом соответствовать постоянной энергии в спектрах, записанных при разных температурах, но изменяться по относительным интенсивностям синхронно по трем группам при изменении температуры, причем так, чтобы с ростом температура росли именно те пики, которые изначально (равно как и впоследствие) являются меньшими по интенсивности. Такое сочетание трех условий создает жесткие ограничения числа вариантов при математической обработке полученных спектров, что позволило получить однозначное разложение полосы при 9-11 эВ на функции Гаусса, выполненное с помощью стандартной программы Origin (рис. 3,4). В результате были получены экспериментальные значения энергий ионизации (ЭИ_эксп) молекулы ДМД как в ее основной конформации (К), так и в двух ее промежуточных твист формах: 2,5-Т и 1,4-Т (табл. 2, рис. 5). Сравнение найденных таким образом величин ЭИ_эксп с аналогичными расчетными ЭИ_расч, полученными методом HF 6-31G^** (табл. 1, рис. 6), выявило хорошее качественное соответствие данных разложения расчетным значениям энергий МО.

Таблица 2. Экспериментальные (ЭИ, метод ФЭС) и расчетные (метод HF 6-31G^**) энергии двух высших занятых молекулярных орбиталей ЗМО₁ и ЗМО₂ - (эВ) для молекулы ДМД

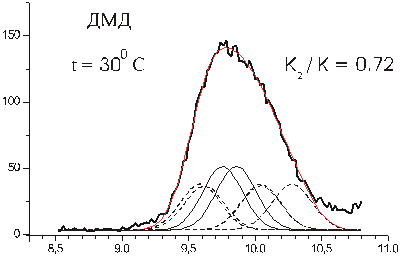
Рисунок 3. Разложение первой полосы ФЭС ДМД при 30⁰С на функции Гаусса

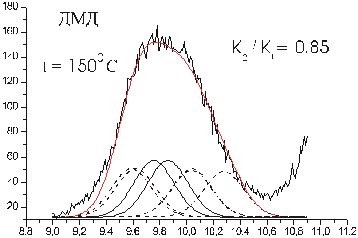
Рисунок 4. Разложение первой полосы ФЭС ДМД при 150⁰С на функции Гаусса

Все в совокупности позволяет сделать важные для настоящей работы выводы о правомерности использованных квантово-химических расчетов, а, следовательно, о справедливости полученных на их основе выводов о характере ППЭ молекул изученного соединения, их конформационной динамике, а также особенностях пространственного и электронного строения.

СПИСОК ЛИТЕРАТУРЫ

1. Гиттинс В.М., Уин-Джонс Е., Уайт Р.Ф. Инверсия колец некоторых шестичленных гетероциклических соединений //Внутреннее вращение молекул /Под ред. В. Дж. Орвилл-Томаса. - М.: Мир, 1977. - С.352-404.
2. HyperChem 5.02. Trial version. http://www.hyper.com/.
3. Курамшина А.Е., Цеплин Е.Е., Бочкор С.А., Хвостенко О.Г., Кузнецов В.В. Региональная школа-конференция для студентов, аспирантов и молодых ученых по математике и физике. Уфа, РИО БашГУ, 2003. С.107-108.

Библиографическая ссылка