Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Краснов И.Ю.

Статья в формате PDF

130 KB

Пусть математическая модель функционирования электромеханического объекта описана системой линейных нестационарных разностных уравнений вида [1]:

 (1)

где x(k) - m-мерный вектор, компоненты которого определяют состояние электромеханического объекта в такт времени k; u(k) - m-мерный вектор управляющих воздействий;  - матрица параметров объектов управления размерности ,  - матрица влияния управляющих воздействий размерности ; x₀ - начальное состояние электромеханического объекта в момент времени t₀ ;

(t₀, N) - период моделирования; такт k соответствует моменту времени  Δt - период квантования сигнала по времени.

Функционал качества имеет вид:

 (2)

Образуем гамильтониан:

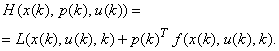(3)

Вспомогательный вектор p(k) является решением разностного уравнения:

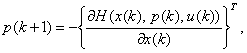
краевое условие которого на правом конце определяется условиями трансверсальности [2].

В качестве управляющего воздействия рассматривается выходное напряжение импульсного преобразователя, модулированное по широтно-импульсному закону и поступающее на исполнительный элемент электромеханического объекта.

В аналитической теории при нахождении управлений, доставляющих минимум функционала качества (2), учитывается то обстоятельство, что на оптимальной траектории управления есть точка стационарности гамильтониана (3) (на управление не наложено ограничений), и не используется тот факт, что вдоль оптимальной траектории гамильтониан принимает вполне определенное значение. Это необходимое условие минимизации функционала положим в основу конструкции алгоритма оптимизации.

В качестве регулятора нестационарной электромеханической системы будем использовать пропорциональный регулятор Беллмана.

Пусть функционал качества имеет вид:

(4)

где матрицы  и Q - положительно полуопределенные ; матрица R - положительно определенная ; время N задано; на управление u(k) ограничений не наложено. Задача заключается в построении такого управления u(k), которое на объекте (1) доставило бы минимум функционалу (4) при влиянии возмущений.

В задаче (1-4) оптимальное управление определяется соотношением [3]:

где K(k) - матрица коэффициентов усиления регулятора размера :

(5)

а матрица P(k) размера  удовлетворяет уравнению:

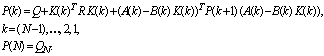
Компенсировать влияние возмущений предлагается за счет выбора параметров матрицы K(k). Запишем матрицу K(k) в виде:

где 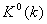 - решение уравнения (5),  - матрица , отыскиваемая алгоритмическим способом.

Гамильтониан при этом будет иметь вид:

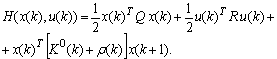
Алгоритм оптимизации системы имеет вид:

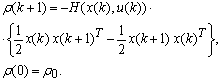
Проведём анализ синтезированного алгоритма (реакцию системы на изменение параметров объекта). Будем считать, что объектом управления является двигатель постоянного тока ДК-1, момент инерции которого подвергается скачку величиной в 5 раз меньше своего номинального значения. Переходные процессы по скорости двигателя с вынужденными возмущениями в момент времени  k=100 (0.2 сек.), изображены на рисунке.

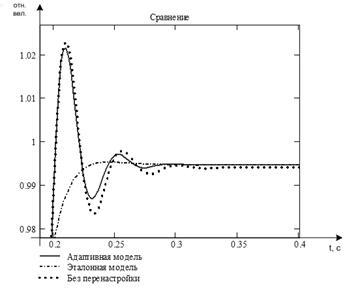
Рисунок 1. Переходные процессы по скорости двигателя с вынужденными возмущениями в момент времени  k=100 (0.2 сек.)

Установившееся значение переходного процесса по скорости в модели без перенастройки параметров регулятора много меньше по сравнению с эталонной моделью. Значение же в модели с перенастройкой полностью совпадает с эталонным значением. Таким образом, можно заключить, что построенный алгоритм полностью компенсировал влияние возмущений.

Ещё недавно грубые системы, сохраняющие характеристики при неизбежных отклонениях параметров от расчетных значений проектировались, как правило, "на ощупь" простым подбором параметров при моделировании, поскольку регулярных процедур проектирования в большинстве случаев не было.

В современной теории управления электромеханическими объектами всё больше и больше внимания уделяется чувствительности алгоритмов к возмущениям.

СПИСОК ЛИТЕРАТУРЫ

1. Сю Д., Мейер А. Современная теория автоматического управления и ее применение. - М.: Машиностроение, 1972. - 544 с.
2. Афанасьев В.Н., Букреев В.Г., Зайцев А.П., Степанов В.П., Титов В.С. Электроприводы промышленных роботов с адаптивным управлением. - Томск.: Изд-во Том. Ун-та, 1987. - 165 с.
3. Алгоритм оптимального управления нестационарными электромеханическими объектами //Материалы IV Всероссийской науч.-технич. конф. (ИАМП-2003) «Измерения, автоматизация и моделирование в промышленности и научных исследованиях». - Бийск, 2003. - С. 8-11.

Библиографическая ссылка