. Работу бросания считают равной 
. В этих безобидных, на первый взгляд, утверждениях, содержится нечто, противоречащее одному из положений физики. В физике используется понятие КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ (η ) - КПД. КПД не может быть больше единицы. КПД всегда меньше единицы, поскольку часть энергии превращается тоже в энергию, но не в ту, что нужна, и поэтому теряется для полезного использования. КПД всегда меньше единицы вследствие самой физической природы вещей и явлений. Если же записать КПД для выше приведенных случаев подъема тела на высоту h, то получим: 
. Рассмотрим более подробно ряд случаев подъема тела на высоту h.
§ 1. Рассмотрим движение тела, брошенного вертикально вверх с начальной скоростью V0, за счет действия мгновенной силы в виде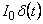 
[5, 6] , где 
- δ- функция Дирака [7, 8]. Величину I0 будем называть единичным импульсом силы, численно равным количеству движения (импульсу), полученным телом I0=mV0. Дифференциальное уравнение движения (II закон Ньютона) имеет вид:
(1)
при нулевых начальных условиях:
; 
(2)
Где x- вертикальная координата, отсчитываемая от поверхности Земли. Для решения задачи воспользуемся двусторонним преобразованием Лапласа [9]
(3)
Для решения этой задачи используется дифференциальное уравнение для односторонней функции 
где H(t) - единичная (ступенчатая) функция Хевисайда [8, 9]. Тогда производные функции x*(t) имеют вид [9]
;
После соответствующих преобразований, решение получается в следующем виде
(4)
Вычислим работу, совершаемую силами
(5)
Вычисляя интегралы, получим [9]
;
;
;
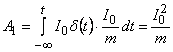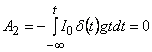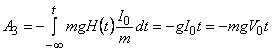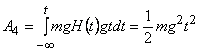
Работа, совершаемая силами, запишется в виде:
(6)
Работа, совершенная единичным импульсом силы I0=mV0 (или начальная энергия, полученная телом) будет равна
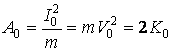(7)
где 
- начальная кинетическая энергия тела. Время подъема до максимальной высоты 
, а максимальная высота подъема 
. Подставляя в выражение (6) значение t0, получим конечное значение совершенной работы:
(8)
Поскольку начальная энергия полученная телом A0=2K0, то КПД процесса бросания тела вертикально вверх будет равен
То, что начальная энергия тела A0=2K0 можно объяснить эффектом удвоения массы (силы тяжести) в случае внезапно приложенной нагрузки при бросании [5, 10].
§ 2. Рассмотрим случай движения тела вертикально вверх под действием постоянной вертикальной силы тяги FT. Уравнение движения (II закон Ньютона) запишется в следующем виде
(9)
Если FT=mg, то правая часть тождественно равна нулю, и движения тела вверх не происходит, но в этом случае сила давления тела на опору (например, на поверхность Земли) равна нулю, поскольку сила тяги нейтрализует «тяжелую» массу, и тело находится в квазиневесомом состоянии (состояние левитации). Обозначим силу тяги, равную mg, значком "Л": FЛ=mg. Если сила тяги больше mg на величину ΔF, то уравнение (9) можно переписать в виде
или 
(10)
Таким образом, часть силы тяги FЛ =mg не будет принимать непосредственного участия в работе по подъему тела вверх. Тело будет подниматься вверх только благодаря действию силы ΔF с ускорением 
. За время t высота подъема будет равна
(11)
Работа подъема составит величину, равную
(12)
Поскольку 
есть импульс силы, численно равный импульсу (количеству движения), полученному телом 
, где V1 - скорость тела в момент времени t, то можно записать 
.
Однако чтобы остановить тело на данной высоте h, необходимо еще совершить работу торможения, численно равную кинетической энергии, приобретенной телом 
;
(13)
Отдельного разговора заслуживает вопрос о том, что же делает другая часть силы тяги FЛ=mg? Ведь она не принимает участия в подъеме тела на высоту h, она лишь нейтрализует силу тяжести, обеспечивая условия левитации. Можно записать баланс импульсов сил в виде:
(14)
Возведя обе части равенства в квадрат и разделив на 2m, получим баланс энергий (работ):
(15)
Работу, совершаемую силой FT, можно переписать в следующем виде:
(16)
Или, с учетом выражений (11) и (12):
(17)
Первый член в правых частях выражений (15)-(17) представляет собой работу силы левитации в стационарном (неподвижном) состоянии
(18)
Второй член выражает работу, связанную с ускоренным перемещением силы левитации
(19)
Третий член - это обычная работа силы ΔF, обеспечивающей ускоренное движение тела в соответствии со II законом Ньютона:
(20)
Произведение работ 
. На рис. 1 показана зависимость величины работы левитации AЛ от величины работы AΔ, выраженных в долях потенциальной энергии mgh.
Выражение (17) имеет минимум, равный 
при 
. На графике (рис. 2) показана зависимость работы 
, совершаемой силой тяги FT, выраженной в долях потенциальной энергии П=mgh, от величины соотношения ΔF / mg. Если использовать обычную формулу определения работы подъема тела на высоту h с некоторым ускорением a, то будем иметь A=m(g+a)h = (FЛ + ΔF)h . Ее зависимость от величины соотношения ΔF / mg показана на графике (рис. 3). Самое нелепое на этом графике то, что при ΔF=0 совершается работа подъема, равная mgh, хотя, согласно условиям статики, тело должно оставаться неподвижным.
Отрицательная работа, совершаемая силой тяжести при подъеме тела вверх вовсе не равна mgh. Она равна
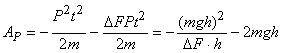(21)
Сумма работ (17) и (21) дает величину 
, т.е. величину кинетической энергии, приобретенной телом на высоте h.
КПД подъема при без учета работы торможения составляет 
.
§3. Тело находится в состоянии левитации (приложена сила тяги 
). Для того, чтобы тело двигалось вверх, в начальный момент времени на тело действует направленный вверх единичный импульс силы 
. В этом случае дифференциальное уравнение движения запишется в виде
(22)
при нулевых начальных условиях. Решая уравнение с помощью преобразования Лапласа, получим
(23)
Вычисляем работу, совершаемую всеми силами
(24)
где 
, а t1 - время движения до высоты 
. Вычисляя интегралы, выделим положительную и отрицательную работы
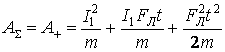(25)
(26)
Преобразуем выражения, входящие в (25)
, где 
Тогда суммарную положительную работу (работу подъема) можно записать в виде
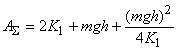(25а)
Эта работа имеет минимум, равный 
при величине 
. График зависимости суммарной работы подъема AΣ в зависимости от величины 2K1, выраженных в долях потенциальной энергии П=mgh, показана на графике (рис. 4). Отрицательная работа, совершаемая силой тяжести (27), может быть представлена в виде:
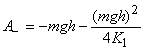(26а)
При больших значениях начального импульса (
) она асимптотически стремится к своему обычному значению 
.
Величина энергии, приобретенной в результате ударного нагружения мгновенным импульсом силы I1=mV1, равна 
. Двойная энергия является результатом удвоения массы при внезапно приложенной нагрузке (в рамках модели материальной точки). В рамках реального упругого тела половина энергии идет на возбуждение упругих колебаний, которые вследствие дисперсии и внутреннего трения с течением времени затухают, переходя во внутреннюю энергию (тело нагревается).
СПИСОК ЛИТЕРАТУР
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. средн. шк. - М.: Просвещение, 1990.
- Сивухин Д.В. Общий курс физики. Том I. Механика. - М.: Наука, 1989.
- Детлаф А.А., Яворский Б.М. Курс физики. Учебн. пособие для вузов. - М.: Высш. шк., 1989.
- Матвеев А.Н. Механика и теория относительности: Учебн. пособие для физ. спец. вузов. - М.: Высш. шк., 1986.
- Иванов Е.М. Дополнительные главы классической механики: - Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических //Успехи современного естествознания, № 9, 2004.
- Арсенин В.Я. Математическая физика. - М.: Наука, 1966.
- Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970.
- Б. Ван Дер Поль, Х. Бреммер. Операционное исчисление на основе двустороннего преобразования Лапласа. - М.: Изд. Иностр.Лит. 1952.
- Иванов Е.М. Закон инерции Галилея (I закон Ньютона) //Вестник ДИТУД, № 1, 2003.
Библиографическая ссылка
Иванов Е.М. РАБОТА ПОДЪЕМА ТЕЛА В ОДНОРОДНОМ ПОЛЕ ТЯЖЕСТИ // Современные наукоемкие технологии. – 2005. – № 3. – С. 9-12;URL: https://top-technologies.ru/ru/article/view?id=22372 (дата обращения: 03.12.2024).