Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Кириллов Ю.В. Кудаев С.А.

Статья в формате PDF

186 KB

1. Введение

В современных условиях энергетические предприятия вынуждены строить свою работу с учетом конъюнктуры рынка энергоносителей, который в последнее время неуклонно расширяется. Например, предприятие ОАО «Новосибирскэнерго» ТЭЦ-2 закупает энергетический уголь на угольном рынке Кузбасса, который сегодня представляет собой 10 крупных угольных компаний, ряд самостоятельных фирм, объединяющий 47 шахт и 26 разрезов, 40 обогатительных фабрик и установок, а также ряд более мелких предприятий. Все они предлагают широкий ассортимент своей продукции - углей различных сортов, разной цены и соответствующего качества.

В условиях несвоевременной оплаты конечными потребителями услуг за произведенную электроэнергию ОАО «Новосибирскэнерго» часто испытывает финансовые затруднения и поэтому вынуждено закупать более дешевый, но некачественный уголь. Однако, как выяснили специалисты ТЭЦ, это приводит к тому, что возрастают удельные затраты на производство тепло- и электроэнергии в то время, как выход конечной продукции уменьшается. Более того, по подсчетам специалистов ОАО «Новосибирскэнерго», иногда убытки энергосистемы из-за потребления некачественного угля превышают выигрыш от покупки более дешевых энергоносителей.

Отсюда возникает задача оптимального выбора энергопредприятиями таких сортов угля, при использовании которых будет найден компромиссный вариант из следующих альтернатив:

а) максимизация прибыли от производства тепловой и электрической энергии;

б) минимизация затрат на закупку и транспортировку энергоносителей;

в) минимизация затрат на потери при производстве тепло- и электроэнергии, связанные с качеством потребляемого угля.

Задачи такого рода являются многокритериальными (векторными) задачами оптимизации, оригинальный алгоритм решения которых был предложен в [1] и развит в [2]. В данной работе рассмотрен числовой пример его реализации для решения важной прикладной задачи.

2. Постановка векторной задачи

Пусть  - доля количества угля i-го сорта в общем объеме закупаемых энергоносителей, а p_i - цена за 1тонну соответствующего сорта, включая транспортировку. Качество угля определяется двумя основными параметрами: a_i - % содержания золы и b_i - % содержания влаги в единице веса i-го сорта. Для нормальной работы оборудования ТЭЦ-2 установлены соответствующие нормативы на допустимые значения этих параметров: a₀=16% и b₀=8%. Специалистами ТЭЦ-2 были рассчитаны коэффициенты удельного выхода электрической (d_i ) и тепловой энергии (c_i ) при сжигании в котлоагрегатах 1 тонны угля i-го сорта. Значения этих параметров для основных сортов используемого угля приведены в таблице 4.1

Таблица 1. Значения параметров для основных сортов используемого угля

Кроме того, были определены коэффициенты потерь, характеризующие уменьшение удельной выработки электрической (K₁ ) и тепловой (K₂ ) энергии при увеличении содержания золы на 1%, а также аналогичные коэффициенты потерь (K₃  и K₄ соответственно) при увеличении содержания влаги на 1%.

Таким образом, необходимо найти компромисс между максимальной выработкой электрической энергии

,                  (2.1)

тепловой энергии

,                           (2.2)

минимумом потерь от увеличения зольности при выработке электроэнергии и тепла

                                   (2.3)

,                                 (2.4)

а также минимумом потерь при выработке тепло- и электроэнергии от увеличения влажности

,                                  (2.5)

,                                  (2.6)

и, конечно, минимумом затрат на покупку и транспортировку

.                   (2.7)

Выбор необходимо сделать при условии, что

.                 (2.8)

При этом нумерация переменных производится в соответствии с порядковым номером сорта угля, представленного в таблице 1. В результате имеем следующую линейную неоднородную задачу векторной оптимизации:

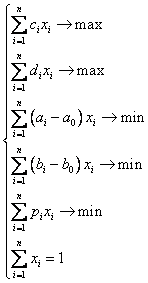                     (2.9)

3. Решение векторной задачи

Используя в (2.9) данные таблицы 1, получаем следующую числовую модель векторной задачи:

                        (3.1)

Решим задачу (3.1) методом гарантированного результата при нормализации критериев (ГРНК) как линейную неоднородную задачу векторной оптимизации с равнозначными критериями [1]. Для автоматизации процесса решения была выбрана программа электронных таблиц Excel 9.0 из пакета MS Office XP (2002). В соответствии с алгоритмом решения таких задач [1]необходимо выполнить следующие этапы вычислений.

1. Решаем скалярные задачи оптимизации для каждого критерия с помощью модуля «Поиск решения» таблиц Excel 9.0 и определяем значения и координаты его максимума и минимума. Получаем:

,

,

   ,

 ,

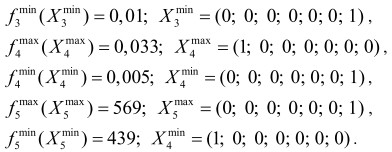
2. Производим нормализацию критериальных функций, получаем их относительные оценки .

3. Формируем λ- задачу для получения единственного Парето-оптимального решения (3.1):

          (3.2)

Решение λ- задачи приведено на рис. 1. Координаты компромиссного решения равнозначной задачи:

.

При этом компромиссные значения относительных оценок критериев будут гарантированно не хуже . Действительно:

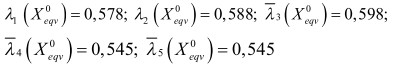
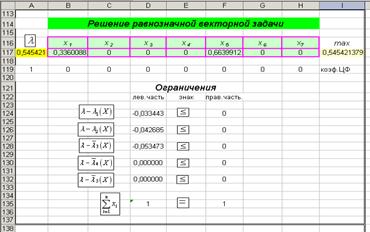
Рисунок 1. Решение - задачи

Таким образом, для получения оптимального решения необходимо закупать уголь 1 сорта в количестве 33,6% от общего объема и 66,4% угля 5 сорта. При этом общие затраты на закупку составят 54,5% от максимальной стоимости, затраты на потери от повышенной влажности составят 54,5% от максимальных, затраты на потери от повышенной зольности составят 59,8% от максимальных, производство тепловой энергии будет на уровне 58,8% от максимума, а производство электроэнергии - на уровне 57,8% от того максимума, который был бы достигнут, если в качестве единственного критерия выбрать только общий объем выработанной ТЭЦ-2 электрической энергии.

4. Поставим теперь задачу улучшить найденное компромиссное решение. Пусть ЛПР желает непременно уменьшить затраты на покупку энергетического угля даже за счет значений по остальным критериям. Для этого, в соответствии с алгоритмом решения неравнозначной линейной задачи векторной оптимизации [2], необходимо увеличить значение относительной оценки по 5-му критерию, ухудшив значения остальным критериев с помощью коэффициентов приоритета 5-го критерия по отношению к ним. Вычисление необходимых пределов коэффициентов приоритета представлено на рис. 2.

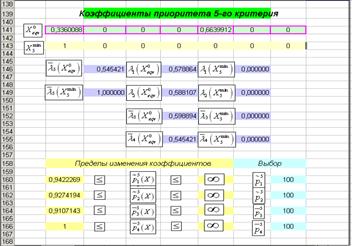
Рисунок 2. Вычисление необходимых пределов коэффициентов приоритета

В результате получим

5. Формируем вектор коэффициентов приоритета в найденных пределах

 и строим λ- задачу с неравнозначными критериями:

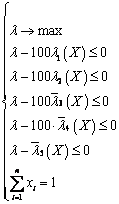                      (3.3)

Решение неравнозначной задачи приведено на рис 3. В результате получим новые координаты Парето-оптимального решения:

.

Т.е., в этом случае угля 1 сорта следует закупать уже в количестве 98,8% от общего объема, а угля 5 сорта только 0,12%. Как видно, значение 5-го критерия явно улучшается и лишь на 1% больше своего локального минимума.

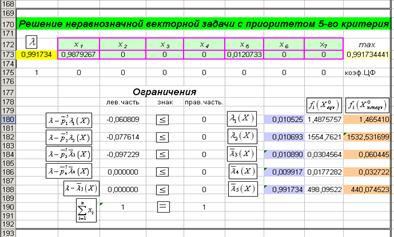
Рисунок 3. Решение неравнозначной задачи

Однако значения других критериев стали хуже: затраты на потери от повышенной влажности и зольности возросли до 99% от максимума, выработка тепловой и электрической энергии снизились до значений лишь на 1% превышающих минимально возможные. Тем не менее, цель достигнута: значение критерия 5 явно улучшилось по сравнению с равнозначной задачей.

4. Выводы

Таким образом, метод ГРНК является действенным инструментом для принятия оптимальных решений в сложных условий многокритериального выбора. Следует отметить, что вычисляемые коэффициенты приоритета являются эффективным средством целенаправленного изменения значений компромиссного решения, в первую очередь его улучшения. Это является дополнительным плюсом для практического использования алгоритмов метода ГРНК, так как значительно снижает субъективизм в принятии решений по такому важному вопросу, как приоритет определенного критерия.

СПИСОК ЛИТЕРАТУРЫ 

1. Иванов Л.Н., Кириллов Ю.В. К вопросу о Парето-оптимальности решений задач векторной оптимизации // Сборник научных трудов НГТУ, 2003, №3, стр. 61-74.
2. Кириллов Ю.В. Методы многокритериальной оптимизации в информационных технологиях анализа инновационной деятельности // «Актуальные проблемы электронного приборостроения» АПЭП - 2004: Тр. VII междунар. конф., Новосибирск, 21-24 сент., 2004 - Изд-во НГТУ, 2004. - Т. 7. - стр. 84 - 88.

Библиографическая ссылка