К пластическим средам относятся такие, у которых упругие деформации пренебрежимо малы [1]. Однако, именно упругие деформации оказывают существенное влияние на характер деформационного поведения тиксотропных пластических дисперсных сред, что обусловливает особенность их сдвигового течения в сквозных каналах измерительных приборов и технологического оборудования.
Особенностью сплошных пластических сред является то, что их течение в сквозных каналах характеризуется соотношением упругости и пластичности, количественная величина которого изменяется в зависимости от скорости сдвига.
Кроме этого, при течении в трубах межоперационного транспорта, в сквозных каналах формующих прессов и других рабочих зонах технологического оборудования пластические дисперсные среды проявляют эффект пристенного скольжения, или П - эффект, который необходимо учитывать в инженерных расчетах, поскольку он влияет на производительность.
Графики кривых течения пластических сред, получаемые в широком диапазоне скоростей сдвига, как правило, не только нелинейные, но и имеют кривизну разного направления. При этом выпуклость участка графика кривой течения может быть обращена к оси касательного напряжения или к оси скорости сдвига.
Участки нелинейных графиков кривых течения пластических сред в логарифмических координатах lg θ = lg θ (lg γ), обращенные к разным осям координат разделяются точкой смены направления кривизны, так называемыми точками перегиба.
На рисунке 1 представлены схемы характерных графиков кривых течения пластических сред в безразмерных координатах с точками перегиба А и В, в которых происходит смена направления кривизны графиков lg θ = lg θ (lg γ), Из рисунка 1 видно, что с увеличением скорости сдвига γ направление выпуклости графика кривой течения (1) в точке А(20, 8) изменяется с направления к оси lg θ на направление к оси lg γ. А направление выпуклости графика кривой течения (2) изменяется в точке В(20, 3) в обратной последовательности, то есть с направления к оси lg γ на направление к оси lg θ.
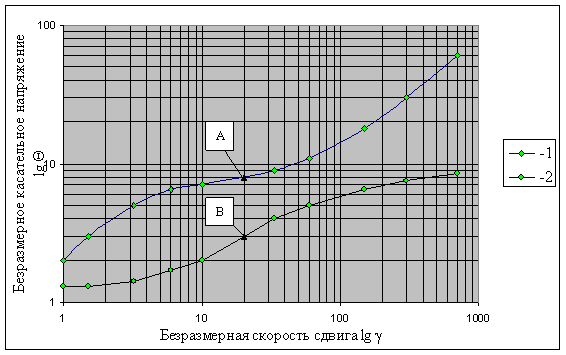
Рисунок 1. Схемы графиков кривых течения в логарифмических координатах
Для обозначения направления кривизны участков графиков кривых течения lg θ = lg θ (lg γ´), введем знаки «+» и «-». При этом если кривая течения обращена выпуклостью к оси lg γ, ей присваивают знак «+», а если кривая течения обращена выпуклостью к оси lg θ - знак «-». Эти же знаки следует учитывать при написании реологических уравнений состояния пластичных материалов, проставляя их перед основной реологической характеристикой пластичных материалов - предельным напряжением сдвига θ0, поскольку на кривизну зависимостей касательного напряжения от скорости сдвига в логарифмических координатах влияет θ0.
Если в реологические уравнения состояния входят символы предельного напряжения сдвига θ0 со знаками ±θ0 и -+θ0, то это означает следующее. Данные реологические уравнения состояния соответственно описывают кривые течения пластичных сред с точкой перегиба, в которой изменяется направление выпуклости графика lg θ = lg θ (lg γ), от оси lg γ к оси lg θ и от оси lg θ к оси lg γ.
Для кривых течения с точками перегиба обозначение смены направления кривизны графиков (1) и (2) с целью упрощения написания уравнений можно выполнить индексами α и β при символе предельного напряжения сдвига θ0:
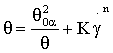 или
или 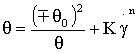 ; (1)
; (1)
 или
или 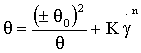 , (2)
, (2)
где 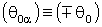 и
и 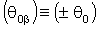 .
.
На рисунках 2, 3 и 4 представлены экспериментальные кривые течения полиэтилена [2], ацетат целлюлозы [3], консистентных смазок [4] и некоторых кондитерских сред [5, 6, 7], которые по характеру кривизны графиков относятся к первой и второй группам и могут быть описаны соответствующими реологическими уравнениями состояния (1) или (2).
Кривые течения 1, 2а; 1,2 б и 2в, изображенные на рисунке 2, а также кривая течения 1 - на рисунке 3 относятся к первой группе и описываются реологическим уравнением состояния (1). Эти графики кривых течения показывают, что с ростом скорости сдвига происходит смена упруго-вязкого течения на пластично - вязкое.
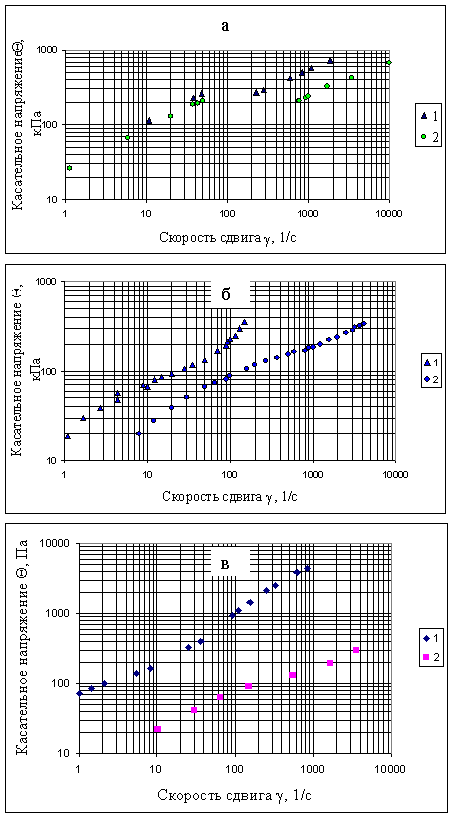
Рисунок 2. Кривые течения: а - линейного полиэтилена при отношении длины капилляра к диаметру: 1 - 3,65 и 2 - 16 (температура 152 оС) [2]; б - ацетат целлюлозы при температуре: 1 - 190 оС и 2 - 210 оС [3]; в - 1 - смазки ГОИ - 54п при температуре 15оС и 2 - солидола жирового при температуре 20оС [4].
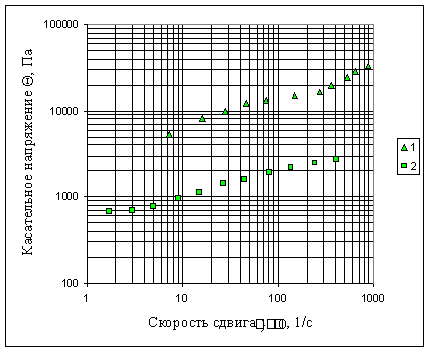
Рисунок 3. Кривые течения: 1 - песочное тесто с 20% яблочной пасты, 2 - жировая начинка для вафельных изделий [5, 6].
Кривая течения ржаного теста с отрубями для коржиков (рисунок 4) подобна кривой течения для жировой начинки, представленной на рисунке 3б, и может быть описана с высокой точностью реологическим уравнением состояния (2).
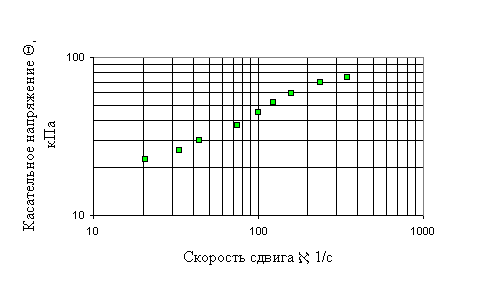
Рисунок 4. Кривая течения ржаного теста для коржиков - с 10% отрубей.
Кривые течения 1 и 2 (рисунок 2в) и (рисунок 3), включая кривую течения на рисунке 4, в области малых значений скорости сдвига обращены выпуклостью к оси скорости сдвига. С ростом скорости сдвига кривизна графика меняется на противоположное направление и для данных кривых течения предлагается реологическое уравнение состояния (2). Такая очередность знаков у символа предельного напряжения сдвига 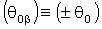 в реологическом уравнении состояния указывает на преобладание пластических свойств, проявляемых средой при течении в диапазоне малых значений скорости сдвига. С ростом скорости сдвига пластично-вязкое течение среды меняется на упруго-вязкое с отрицательным значением предельного напряжения сдвига, что говорит о превосходящих упругих свойствах, проявляемых средой в области высоких скоростей сдвига.
в реологическом уравнении состояния указывает на преобладание пластических свойств, проявляемых средой при течении в диапазоне малых значений скорости сдвига. С ростом скорости сдвига пластично-вязкое течение среды меняется на упруго-вязкое с отрицательным значением предельного напряжения сдвига, что говорит о превосходящих упругих свойствах, проявляемых средой в области высоких скоростей сдвига.
На рисунках 5 и 6 приведены схемы кривых течения, изображенные в прямоугольной декартовой системе координат и относящиеся к первой и второй группам, что соответствует реологическим уравнениям состояния (1) и (2).
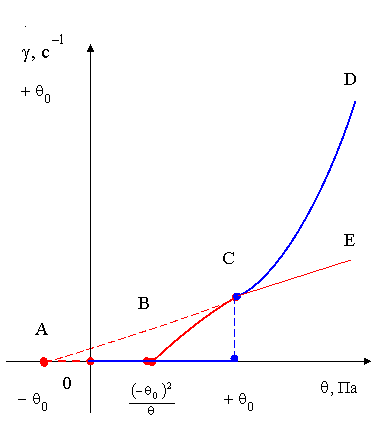
Рисунок 5. Схема кривой течения упруго - вязко - пластической среды
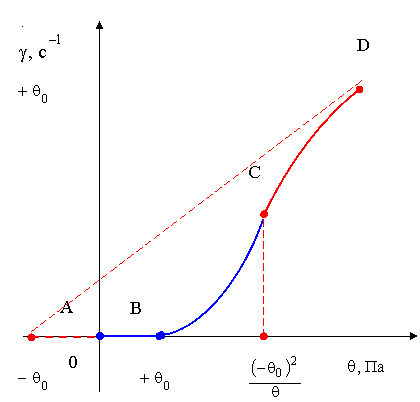
Рисунок 6. Схема кривой течения пластично - вязко - упругой среды
Из рисунков 5 и 6 очевидно пояснение знаков «+» и «-» перед символом предельного напряжения сдвига.
Определим производительность сквозных каналов с круглым профилем поперечного сечения при течении в них дисперсных сред с учетом пристенного скольжения. С этой целью запишем уравнение Навье - Стокса в напряжениях на ось z канала:
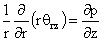 (3)
(3)
После интегрирования (3) получим:
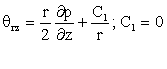 (4)
(4)
Реологическое уравнение состояния (1) запишем в виде:
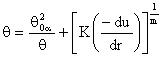 (5)
(5)
где ![]() - величина, обратная индексу течения.
- величина, обратная индексу течения.
Преобразуем (5) с учетом (4), получим дифференциальное уравнение течения пластической среды в сквозном канале с круглым профилем поперечного сечения:
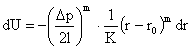 (6)
(6)
Решением (6) с учетом граничных условий:
при 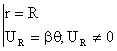
будет:
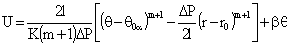 (7)
(7)
где β - коэффициент скольжения, учитывающий П - эффект.
Выражение расхода определим как сумму центрального квази - твердого ядра и периферийной кольцевой области:
![]() (8)
(8)
Скорость ядра потока:
Расход центральной части потока:
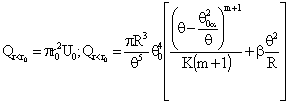 (9)
(9)
Расход периферийной части
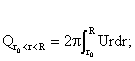
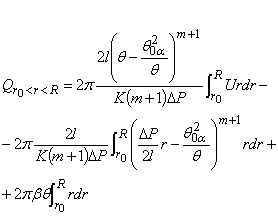 (10)
(10)
Решением (10) будет:
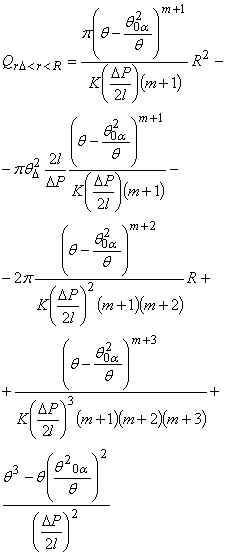 (11)
(11)
Расход по всему круглому поперечному сечению канала с учетом эффекта пристенного скольжения (П-эффект):
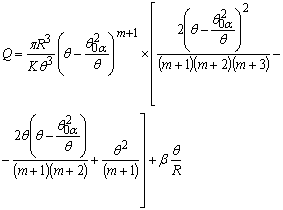 (12)
(12)
По уравнению (12) можно определить производительность сквозных каналов с учетом эффекта пристенного скольжения пластической среды относительно стенки канала.
Пристенное скольжение или П-эффект является характерным для пластических дисперсных сред. Если напряжение на стенке канала не превосходит значения предельного напряжения сдвига пластической среды, то сохраняется внутренняя структура среды и пластическая среда скользит по стенкам сквозного канала подобно твердой пробке. Повышение нагрузки приводит к переходу через предел пластической прочности среды вблизи стенки канала и в пристенной области возникает вязкое течение, а область неразрушенной структуры сохраняется вблизи оси потока, начиная с того значения радиуса, на котором напряжение сдвига достигает значения предельного напряжения сдвига дисперсной среды. Механизм пристенного скольжения характерен для высоконаполненных полимеров, консистентных смазок и широкого спектра пищевых дисперсных материалов, обладающих пластическими свойствами.
Список использованной литературы
- Тябин Н.В. Реологическая кибернетика, часть 1. - Волгоград.: Волгоградская правда, 1977. - 111 с.
- Торнер Р.В. Теоретические основы переработки полимеров. - М.: Химия, 1977. - 462 с.
- Бернхард Э. Переработка термопластичных материалов. - М.: Химия, 1965. - 747 с.
- Фройштетер Г.Б., Трилиский К.К., Ищук Ю.Л., Ступак П.М. Реологические и теплофизические свойства пластичных смазок. - М.: Химия, 1980. - 175 с.
- Корячкин В.П., Ермолаев В.Д. Расчет параметров свойств пищевых систем. Кемерово.: ЦНТИ, 1982. - № 297. - 3 с.
- Корячкин В.П., Мачихин Ю.А. Комплект макетов устройств для анализа качества формования кондитерских масс в изделия.// Новые методы контроля технологических процессов и качество продукции: Сборник научных трудов: - Новосибирск: СО РАСХН, 1991.
- Корячкин В.П. Установка для обработки пищевых сред давлением // Индустрия образования: Сборник статей. Выпуск 3. - М: МГИУ, 2002. - С. 105 - 110.
Библиографическая ссылка
Корячкин В.П. ОСОБЕННОСТИ СТАЦИОНАРНОГО ТЕЧЕНИЯ СПЛОШНЫХ ПЛАСТИЧЕСКИХ СРЕД В СКВОЗНЫХ КАНАЛАХ С УЧЕТОМ ЭФФЕКТА ПРИСТЕННОГО СКОЛЬЖЕНИЯ // Современные наукоемкие технологии. 2004. № 2. С. 12-18;URL: https://top-technologies.ru/ru/article/view?id=21606 (дата обращения: 06.02.2026).



