Введение
Автоматизация технологических операций, связанных с управлением исполнительными механизмами, требует применения алгоритмов, обеспечивающих точное позиционирование и устойчивость к внешним возмущениям [1]. При выполнении пространственных траекторий, характерных для сварочных и смежных производственных процессов, особое значение приобретают методы, позволяющие учитывать кинематические ограничения оборудования, а также влияние случайных факторов среды [2]. В этой связи актуальной задачей является построение алгоритмов управления, способных адаптироваться к изменяющимся условиям и сохранять заданную точность движения [3].
Одним из подходов к решению данной задачи является использование моделей прямой и обратной кинематики в сочетании с методами интеллектуальной коррекции траектории [4]. Применение нечеткой логики позволяет учитывать неопределенность входных параметров и формировать корректирующие воздействия на основе экспертных правил [5], тогда как фильтрация измерений с использованием алгоритма Калмана обеспечивает снижение влияния шумов и погрешностей сенсорных данных [6]. Совместное использование этих методов создает основу для устойчивого управления манипуляционным модулем в условиях нестабильной среды [7].
Настоящая работа посвящена исследованию комплексного алгоритма управления движением манипулятора, реализующего адаптивное следование заданной траектории в пространстве. Рассматривается структура управления, включающая решение задач кинематики, оценку внешних условий и поэтапную коррекцию положения исполнительного органа. Эффективность предложенного подхода анализируется на основе результатов моделирования различных траекторий, отличающихся геометрией и числом шагов дискретизации [8].
Цель исследования – разработка и анализ алгоритма управления манипуляционным модулем, обеспечивающего адаптивное следование заданной пространственной траектории с учетом кинематических ограничений, влияния внешних возмущений и погрешностей измерений, за счет совместного использования моделей прямой и обратной кинематики, методов нечеткой логики и фильтрации состояний.
Материалы и методы исследования
Исследование выполнено методом программного моделирования управления манипуляционным модулем, предназначенным для выполнения заданных пространственных траекторий. Объект управления описывается кинематической моделью, включающей несколько звеньев с поступательными и вращательными степенями свободы [9]. Для определения положения исполнительного органа использовались модели прямой и обратной кинематики, обеспечивающие пересчет пространственных координат в параметры конфигурации привода для каждой точки дискретизированной траектории [10].
Для повышения точности и устойчивости управления в условиях внешних возмущений и погрешностей измерений применялся комбинированный алгоритм коррекции, основанный на методах нечеткой логики [11] и фильтрации состояний [12]. Нечеткая логика использовалась для формирования корректирующих воздействий на траекторию с учетом неопределенных входных параметров, а рекурсивный фильтр Калмана – для сглаживания координат и компенсации шумов сенсорных данных. Эффективность предложенного подхода оценивалась по результатам моделирования движения манипулятора по траекториям различной геометрии с анализом отклонений фактического положения от заданного.
Код был написан на языке Python, в котором были использованы библиотеки NumPy для математических операций и Matplotlib для создания графиков. Для проверки программы был составлен соответствующий метод, который включает метрики, описанные в соответствующем разделе.
Результаты исследования и их обсуждение
Управление манипулятором построено на решении обратной задачи кинематики, что является распространенным подходом при формировании траекторий движения исполнительных механизмов [10]. Для компенсации возмущений и обеспечения устойчивости используется фильтр Калмана [6], а также алгоритм нечеткой логики для оценки неопределенных условий среды [11].
Объект управления – манипуляционный модуль, описываемый последовательностью кинематических звеньев, имеющих как вращательные, так и поступательные степени свободы. Геометрические параметры звеньев задаются в виде трех линейных размеров (обозначенных как L₁, L₂, L₃), соответствующих длинам плечевой, локтевой и конечной секций манипулятора. Исходное состояние представлено начальными углами поворота θ₁, θ₂, θ₃ и смещениями d₁, d₂, d₃ вдоль соответствующих осей.
Общий принцип функционирования системы заключается в определении требуемого положения исполнительного органа в пространстве (в терминах координат x, y, z) и автоматическом определении параметров конфигурации привода, необходимых для достижения заданного положения. Это реализуется посредством алгоритмов прямой и обратной кинематики.
Для определения текущего положения манипулятора в рабочем пространстве используется модель прямой кинематики, предполагающая трансляционное смещение конечного звена вдоль каждой из осей, с учетом геометрических характеристик манипулятора:
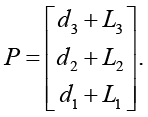 (1)
(1)
Обратная задача кинематики решается аналитическим способом, предполагающим прямой пересчет координат требуемого положения в эквивалентные смещения вдоль каждой оси. Так, зная координаты целевой точки (x, y, z), определяются требуемые значения d₁, d₂, d₃ следующим образом:
d1 = z – L1; d2 = z – L2; d3 = z – L3. (2)
Данная схема реализует управление системой с учетом упрощенной модели манипулятора, пригодной для программной симуляции или базовой реализации в реальном аппарате.
Ввиду возможного появления внешних нестабильностей (например, вибраций, колебаний температуры, изменения микроклимата на производстве) модуль управления содержит подсистему логико-нечеткой оценки и коррекции. Основу данной подсистемы составляет набор продукционных правил вида
ЕСЛИ [ускорение в интервале A] И [температура в интервале B], ТО [изменить скорость движения на V] и [скорректировать угол на Δθ]
Каждое правило характеризуется двумя входными переменными – текущими значениями ускорения и температуры – и парой выходных воздействий. Для описания степеней принадлежности текущих значений входным лингвистическим переменным используется функция принадлежности, реализующая линейную интерполяцию между заданными границами диапазона. Механизм выбора корректирующего воздействия базируется на максимизации степени принадлежности и масштабировании выхода по значению этой степени:
Коррекция скорости: vʹ = v + μΔv,
Коррекция угла: θʹ = θ + μΔθ, (3)
где μ – максимальная степень принадлежности среди всех активных правил [13–15].
Учет шумов и случайных отклонений в показаниях сенсорных систем осуществляется с применением алгоритма рекурсивной фильтрации, основанного на модели Калмана. Для фильтра используется упрощенная двумерная модель состояния, включающая оценки координат (x, y) и их ковариационную матрицу.
На каждом временном шаге выполняются следующие процедуры:
1) предсказание – прогноз следующего состояния на основе текущей оценки и модели движения:
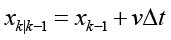 ; (4)
; (4)
2) обновление – учет фактического измерения для коррекции состояния:
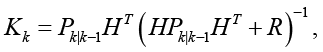 (5)
(5)
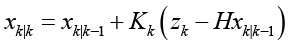 . (6)
. (6)
где Kk – усиление Калмана, P – ковариационная матрица оценки, H – матрица наблюдений, R – ковариация измерений и zk – измерение.
Алгоритм обеспечивает сглаживание траектории и компенсацию помех, возникающих в процессе выполнения манипуляционных операций.
Описанные выше алгоритмы объединяются в единую систему управления движением манипулятора по заданной траектории. На вход подается последовательность координатных точек и ориентиров, соответствующих этапам технологической операции. Для каждой точки производится:
1) вычисление смещений по модели обратной кинематики;
2) оценка внешних условий (ускорение, температура);
3) вычисление корректирующего воздействия на траекторию;
4) фильтрация полученной позиции;
5) формирование обновленного положения для выполнения следующего шага.
Это обеспечивает не только точное следование исходной траектории, но и способность адаптивной подстройки маршрута под влиянием реальных условий среды.
Для демонстрации эффективности построенного управления применяется графическая визуализация исходной и адаптированной траекторий в трехмерной координатной системе. Использование таких средств позволяет наглядно представить степень отклонения и корректировки траектории в условиях действия случайных факторов.
Блок-схема общего алгоритма управления представлена на рис. 1.
Эта блок-схема отражает последовательность действий программы от запуска до завершения, включая взаимодействие с пользователем, генерацию траектории и визуализацию.
Цикл повторяется для каждой точки траектории, определенной числом шагов.
Блок-схема алгоритма адаптации представлена на рис. 2.
Эта блок-схема детализирует процесс адаптации одной точки траектории, включая кинематику, оценку неопределенности и фильтрацию.
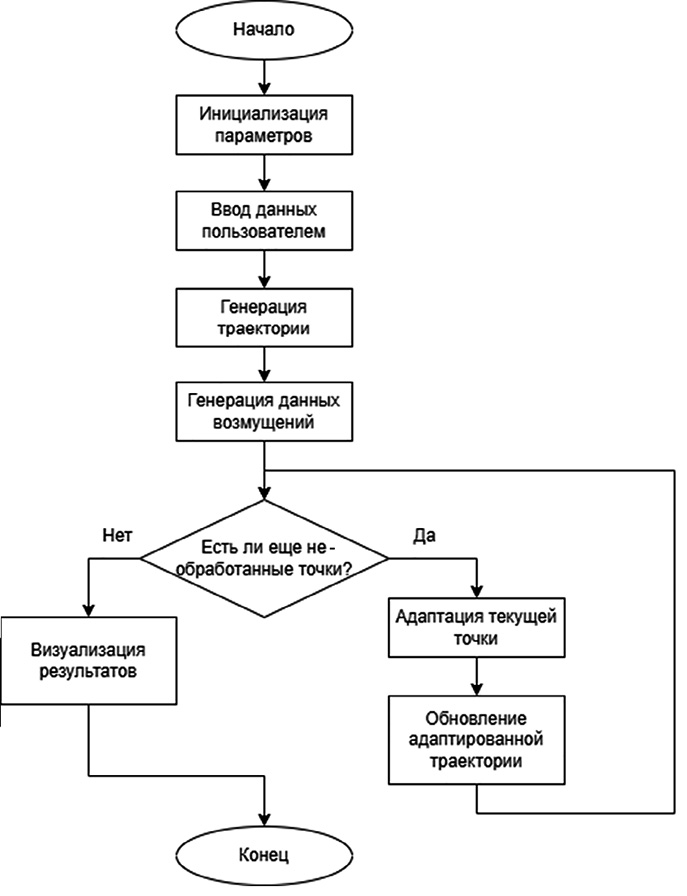
Рис. 1. Схема общего алгоритма управления Примечание: составлен авторами по результатам исследования
Подобная комбинация подходов (фильтр Калмана, нечеткая логика и обратная кинематика) позволяют добиться высокой точности и устойчивости к неопределенностям среды, что подтверждается экспериментально.
В качестве эксперимента был выбран шов длинной 10 см вдоль оси Y. Результаты экспериментов наглядно представлены на рис. 3 и 4.
По графикам можно сделать вывод, что шов получается довольно точным, поскольку максимальное отклонение шва равно 1,5 мм, что входит в допустимый диапазон. Наклонный шов представлен на рис. 5 и 6.
Как видно из графиков, с наклонным швом алгоритм справляется одинаково хорошо. Рассмотрим последний вариант: шов в трех плоскостях. Результат эксперимента представлен на рис. 7.
В рамках этих экспериментов была установлена точность в 100 шагов. Далее будут проведены эксперименты по уменьшению числа шагов и измерению точности алгоритма.
Результаты экспериментов для точности в 10 шагов представлены на рис. 8 и 9.
Как видно из графиков, точность алгоритма не понизилась, но качество шва незначительно пострадало, так как возникает малое пересечение заданной траектории с целевой. Рассмотрим вариант с наклонным швом, который представлен на рис. 10 и 11.
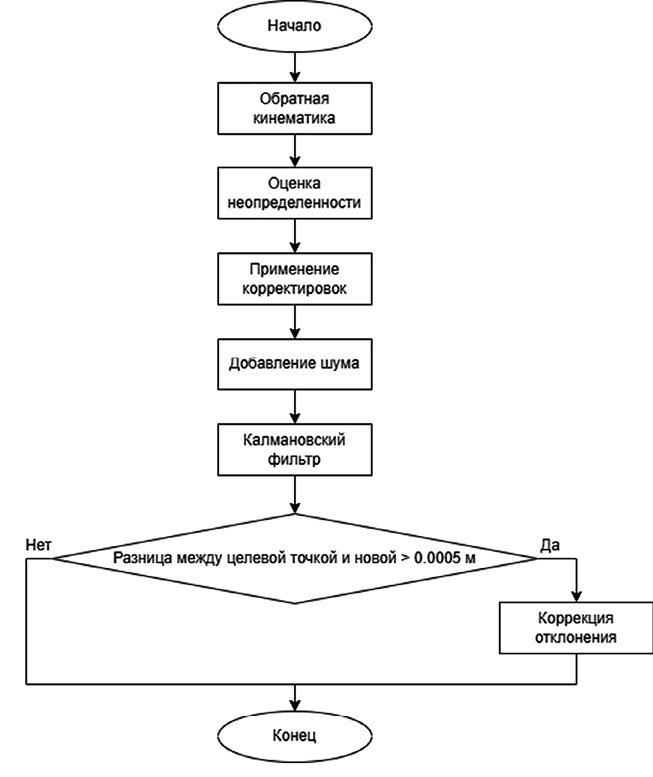
Рис. 2. Схема алгоритма адаптации Примечание: составлен авторами по результатам исследования
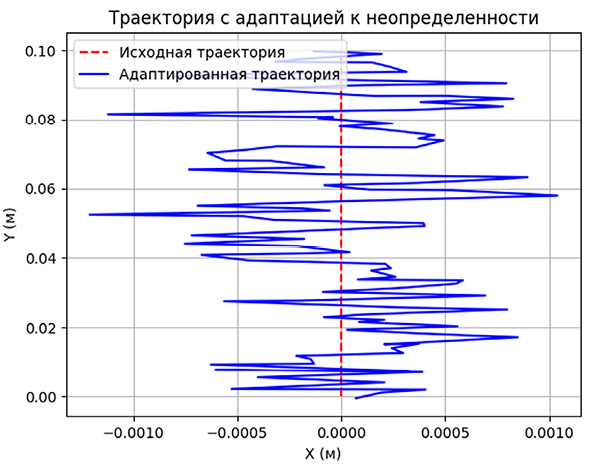
Рис. 3. Результат эксперимента прямого шва на плоскости Примечание: составлен авторами по результатам исследования
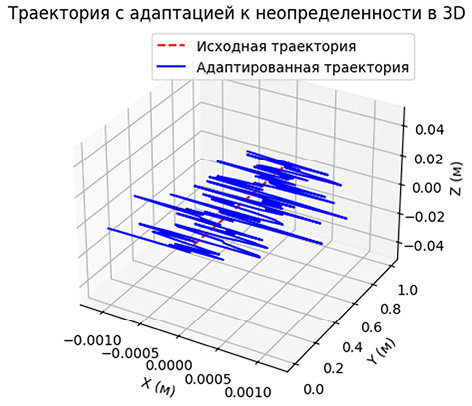
Рис. 4. Результат эксперимента прямого шва в трехмерном варианте Примечание: составлен авторами по результатам исследования
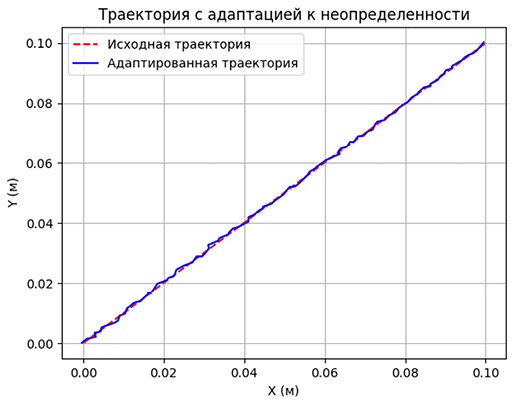
Рис. 5. Результат эксперимента наклонного шва на плоскости Примечание: составлен авторами по результатам исследования
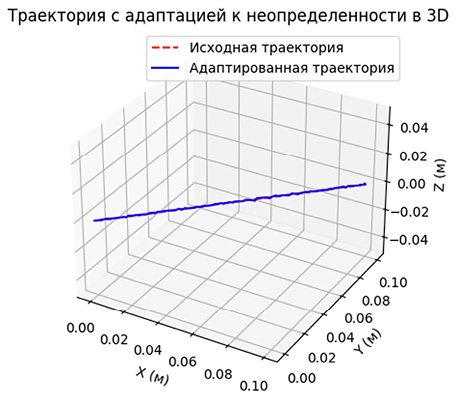
Рис. 6. Результат эксперимента наклонного шва в трехмерном варианте Примечание: составлен авторами по результатам исследования
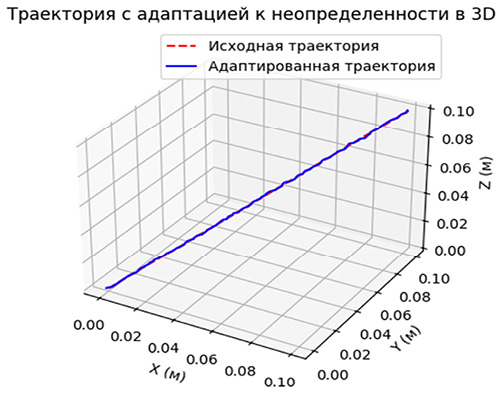
Рис. 7. Результат эксперимента с трехмерным швом Примечание: составлен авторами по результатам исследования
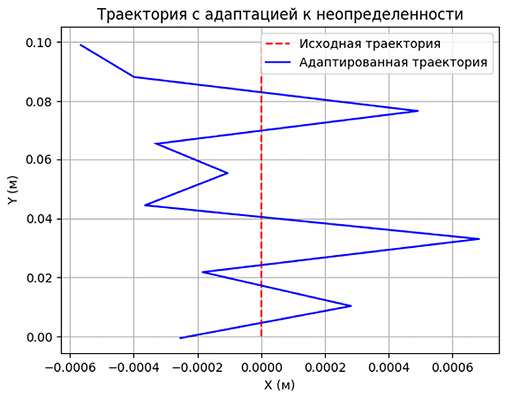
Рис. 8. Результат эксперимента прямого шва на плоскости с точностью 10 шагов Примечание: составлен авторами по результатам исследования
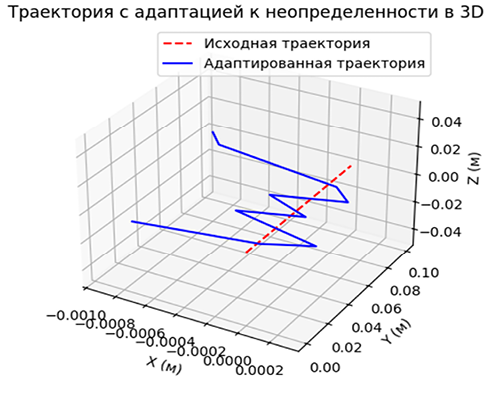
Рис. 9. Результат эксперимента прямого шва в трехмерном варианте с точностью 10 шагов Примечание: составлен авторами по результатам исследования
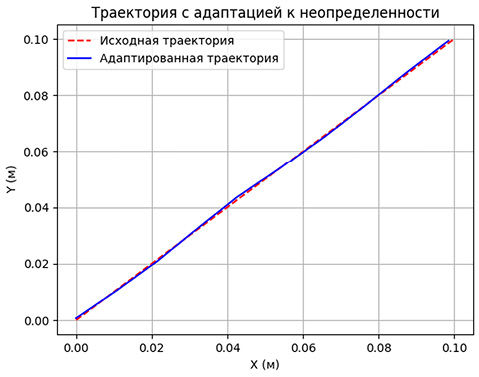
Рис. 10. Результат эксперимента наклонного шва на плоскости с точностью 10 шагов Примечание: составлен авторами по результатам исследования
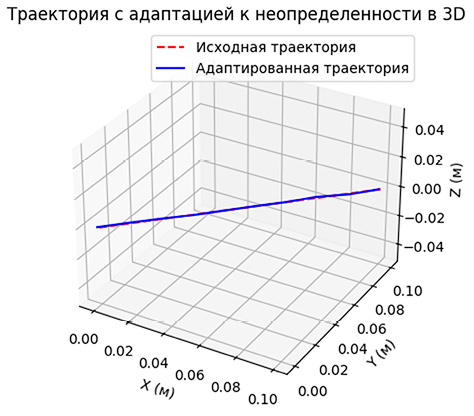
Рис. 11. Результат эксперимента наклонного шва в трехмерном варианте с точностью 10 шагов Примечание: составлен авторами по результатам исследования
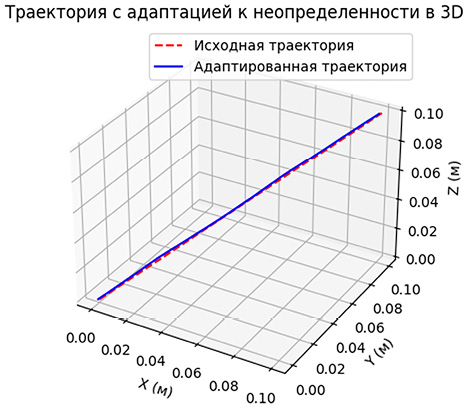
Рис. 12. Результат эксперимента с трехмерным швом с точностью 10 шагов Примечание: составлен авторами по результатам исследования
Шов получился более плавным, относительно варианта с большим количеством шагов. В завершение серии экспериментов рассмотрим трехмерный вариант, который представлен на рис. 12.
Таким образом, можно сделать вывод, что точность не понижается с уменьшением числа шагов, однако уменьшается число пересечений действительной и целевой траекторий шва, что делает во втором случае шов более плавным.
Заключение
В результате проведенного исследования разработан и исследован алгоритм адаптивного управления движением манипулятора, обеспечивающий устойчивое следование сварочным траекториям в пространстве при наличии внешних возмущений и погрешностей измерений. Предложенный подход, основанный на сочетании кинематических моделей, нечеткой коррекции и рекурсивной фильтрации состояний, позволяет формировать корректирующие воздействия в процессе движения и снижать влияние шумов на точность позиционирования исполнительного органа. Результаты программного моделирования для траекторий различной геометрии показали сохранение допустимых отклонений и стабильность работы алгоритма при изменении параметров дискретизации, что подтверждает его применимость для задач автоматизации сварочных операций и целесообразность дальнейшего развития в направлении практической реализации на реальном оборудовании.



