Введение
Переход от школьного курса математики к анализу в вузе стабильно выявляет рассогласование между процедурными навыками и концептуальным пониманием. Исследования показали, что у обучающихся часто возникает разрыв между «образом понятия» и его формальным определением: так, у D. Tall и S. Vinner [1] продемонстрировано, что интуитивные представления о пределе часто не совпадают с ε–δ-определением и систематически порождают ошибки. A. Orton [2] выявил, что дифференцирование нередко осваивается процедурно (по правилам и таблицам) при слабой связке с концептуальной основой. M. Oehrtman в [3] описал типичные ученические метафоры предела («подползание», «бесконечность как большое число»). Отчет [4], опирающийся на крупномасштабные данные, рекомендует вводные диагностические процедуры, адресную поддержку «узких мест» и усиление компонентов, обеспечивающих понимание. В отечественной методической науке также описаны источники трудностей. Так, Г.Е. Полехина [5] систематизирует характерные ошибки при вычислении пределов (подмена «стремится к» на «равно», игнорирование области определения, механические сокращения). Т.Ю. Паршина [6] и Е.В. Пичугина [7] анализируют ошибки при формировании понятия логарифма. В работе [8] М.Г. Токмачев обобщает типичные ошибки по математическому анализу, авторы [9] указывают на проблемы школьного математического образования, связанные со смещением фокуса. Для корректной оценки долей «успеха» в образовательных исследованиях по бинарным исходам целесообразно использовать интервальные оценки с предсказуемым покрытием; сравнительный обзор показывает преимущества интервала Уилсона.
В этой работе авторы помещают эмпирические данные (входной 0-тест на остаточные школьные знания; тематические тесты по пределам и производным) в описанную теоретико-методическую рамку и обосновываем, что устойчивый разрыв «пределы < производные» обусловлен не только «новизной» определения предела, но прежде всего сочетанием факторов школьной подготовки – недостаточной отработанностью алгебраических преобразований (включая логарифмы и преобразование выражений) и фрагментарными знаниями о функции (область определения, свойства, график, поведение на бесконечности).
Цель исследования – обосновать, что более низкая успешность в теме «предел» по сравнению с «производной» проистекает из неумения проводить алгебраические преобразования и поверхностного понимания понятия функции и ее свойств.
Гипотеза исследования – низкая успешность по «пределам» обусловлена недостатками школьной базы – слабыми алгебраическими преобразованиями и фрагментарностью в понимании функции.
Задачи исследования:
− провести 0-тест и тематические тесты по пределам и производным;
− описать распределения результатов и доли «успеха» (≥ 3) с 95 % доверительные интервалы (ДИ) Уилсона;
− сопоставить темы и интерпретировать различия через школьные предпосылки;
− дать рекомендации: школе – логарифмы, преобразования, переводы между представлениями; вузу – концептуальное понимание предела, «каталог» неопределенностей и задачи на выбор метода.
Материалы и методы исследования
В эксперименте участвовало 103 студента-первокурсника Казанского государственного архитектурно-строительного университета. В работе использовался 95 %-й доверительный интервал Уилсона [10] – это score-интервал для доли успеха из биномиальной выборки. В настоящей работе он применен к доле «≥ 3», чтобы корректно отразить неопределенность оценок и сопоставить темы. Эмпирическая база: три последовательных теста – 0-тест (остаточные школьные знания: логарифмы/показательные, квадратные уравнения, неравенства, преобразование дроби), затем тематические по пределам и по производным. Оценивание по шкале 0; 1–2; 3; 4; 5. Основной индикатор – доля «успеха» (балл ≥ 3), согласованная с пятибалльной системой и удобная для практики (выделение зон риска/успешности).
Для каждой доли «≥ 3» рассчитывались 95 % ДИ Уилсона (score-интервал с стабильным покрытием и границами в [0; 1]), что позволяет корректно отражать неопределенность оценки. Дополнительно для наглядности считали «средний аппроксимационный балл» («средний аппроксимационный балл» получают, кодируя категории 0; 1–2; 3; 4; 5 как 0; 1.5; 3; 4; 5 и считая взвешенное среднее. Это компактный индекс уровня (не «средняя отметка»)) – как вспомогательный визуальный показатель.
Предварительное сопоставление тем выполняли графически и при необходимости через χ²-критерий однородности на агрегированных частотах. Надежность обеспечена свойствами интервала Уилсона и согласованностью индикаторов: доли «≥ 3» и аппроксимационный средний балл, удобный для наглядного ранжирования тестов дают одну картину (пределы системно ниже производных). При n ≈ 100 и долях ~0,5–0,6 ожидаемая полуширина ДИ – ≈ 9–10 процентных пункта.
Результаты исследования и их обсуждение
По каждому из трех последовательно выполнявшихся тестов получена согласованная картина, указывающая на специфическую трудность темы «предел» и поддерживающая выдвинутую гипотезу. На 0-тесте (диагностика остаточных школьных знаний) ниже порога «тройки» оказался 41 студент (39,8 %), «ровно 3» – 42 (40,8 %), «4–5» – 20 (19,4 %); следовательно, баллы ≥ 3 набрали 62 из 103 (60,2 %), а 95 % ДИ Уилсона для доли «≥ 3» составил [0,505; 0,691]. На тематическом тесте по пределам ниже 3 баллов – 52 (50,5 %), «ровно 3» – 15 (14,6 %), «4–5» – 36 (35,0 %); итого ≥ 3 набрали 51 из 103 (49,5 %), 95 % ДИ Уилсона [0,401; 0,590]. На тесте по производным ниже 3 – 39 (37,9 %), «ровно 3» – 12 (11,7 %), «4–5» – 52 (50,5 %); итого ≥ 3 – 64 из 103 (62,1 %), 95 % ДИ Уилсона [0,525; 0,709]. По этим интервалам видно, что блок «Пределы» устойчиво слабее «Производных»: центральные оценки различаются (~49,5 % против ~62,1 %), а границы интервалов у «Пределов» заметно смещены вниз; при этом различие между «0-тестом» и «Производными» невелико и по интервалам неочевидно (что согласуется с процедурной «поддержкой» задач на дифференцирование).
На диаграмме долей «≥ 3» с 95 % ДИ Уилсона (рис. 1) видно, что столбец «Пределы» расположен ниже «Производных», а его «вилочка» целиком лежит в области меньших значений. Это означает: если бы при исследовании авторы многократно повторяли измерение на схожих наборах первокурсников, доля успешных по пределам почти всегда была бы заметно ниже доли успешных по производным. Ширина «вилочек» (~±9–10 п.п.) соответствует ожидаемой точности при n ≈ 100 и долях около 0,5–0,6; она не отменяет различия паттернов, а достоверно показывает неопределенность оценки [10].

Рис. 1. Доля ≥ 3 с 95 % ДИ Уилсона по тестам Примечание: составлен авторами на основании данного исследования
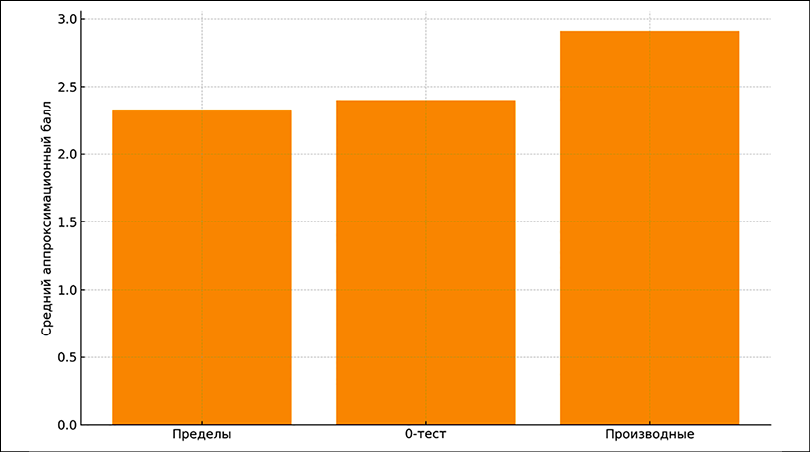
Рис. 2. Средний аппроксимационный балл по тестам Примечание: составлен авторами на основании данного исследования
Смысловое усиление через «средние» аппроксимационные баллы. Для порядковой шкалы 0; 1–2; 3; 4; 5 был вычислен иллюстративный показатель – «средний аппроксимационный балл» (0; 1,5; 3; 4; 5). Он дает компактное ранжирование: Пределы – 2,33 (самый низкий), 0-тест – 2,40 (промежуточный), Производные – 2,91 (самый высокий). Этот индикатор, хотя и аппроксимационный, воспроизводит тот же порядок трудности и подчеркивает, что проседание возникает именно на «пределах», а не представляет собой общий провал.
Входной 0-тест показывает, что школьные недочеты сосредоточены прежде всего в алгебраических преобразованиях и логарифмах (см. распределение «0», «1–2» в 0-тесте): это операции, которые необходимы для понимания предельного перехода, согласно [11]. На «Пределах» доля «≥ 3» падает относительно и 0-теста, и «Производных», а интервал Уилсона смещается вниз – что согласуется с идеей, что без преобразований и целостных представлений о функции (область определения, свойства, график, поведение на бесконечности) студент не распознает тип неопределенности и выбирает не тот метод. На «Производных» картина лучше именно потому, что ранние задачи решаемы по процедурам (правила и таблицы), то есть при слабом концептуальном компоненте [12] возможна «процедурная компенсация».
Полученные результаты согласуются с известным тезисом о разрыве между «образом понятия» и определением предела [1]: результаты авторов показывают, что без понимания понятия функции студент не распознает ситуацию предельного перехода. Конкретные ученические метафоры предела, описанные у Oehrtman [3] («подползание», «∞ как большое число»), в данных авторов проявляются как систематические ошибки распознавания неопределенностей и неверный выбор метода. Вывод Orton [2] о процедурной освоенности дифференцирования и слабой связке с определением производной согласуется с тем, что по теме «Производные» результаты лучше, чем по теме «Пределы», что подтверждается интервальными оценками, а не только частотами. Рекомендации MAA-отчета [4] о необходимости входной диагностики и адресной поддержки «узких мест» подкрепляются и анализом авторов. В отечественной литературе Г.Е. Полехина [5] выделяет типичные ошибки по пределам (подмена «стремится к» на «равно», игнорирование ОДЗ, механические сокращения). А Т.Ю. Паршина [6] и Е.В. Пичугина [7] – ошибки при работе с логарифмами и алгебраическими преобразованиями в школе; распределения, полученные авторами, и интервалы указывают на тот же механизм. В отличие от большинства описательных отчетов, авторы используют 95 % ДИ Уилсона для долей «≥ 3», что позволяет достоверно отразить неопределенность и корректно сопоставлять блоки при n ≈ 100. Научная новизна состоит в количественном подтверждении (на единой выборке первокурсников с использованием доли «≥ 3» и 95 % ДИ Уилсона, дополняемой аппроксимационным индексом) ключевой роли алгебраических преобразований и целостных представлений о функции в провалах по теме «Предел».
Результаты показывают системную природу трудностей с темой «Предел» и подтверждают гипотезу о решающей роли алгебраических преобразований и пониманием понятия функции. По всем индикаторам («распределения», доли ≥ 3 с ДИ, аппрокс. средние) «пределы» стабильно ниже «производных» при сопоставимой стартовой базе. Это согласуется с идеей разрыва между «образом понятия» и ε–δ-определением и с наблюдаемыми метафорами, ведущими к ошибкам распознавания предельных ситуаций [1] (см. также [3]). Более высокие результаты по производным объясняются процедурной опорой (правила/таблицы), а не лучшей концептуальной базой.
Содержательно «предел» требует: а) приведения выражения к форме предельного перехода (ОДЗ, свойства, выделение множителей); б) распознавания неопределенности и выбора соответствующего метода согласно [13]. Эти операции повышают когнитивную нагрузку, поэтому школьные недоработки (логарифмы, преобразования, свойства/графики) закономерно «роняют» раздел «Предел». Выявленная цепочка «слабая база → провал на пределах → относительное улучшение на производных» отражает отсутствие указанного перехода [4].
Сопоставление с прежними работами подтверждает как общность, так и специфику: к известным механизмам трудностей с пределом [1] (см. также [3]). добавляется вклад школьных практик – позднее/формальное введение логарифмов и слабая тренировка алгебраических преобразований/ОДЗ [14].
На школьном уровне целесообразно обеспечить более раннее и содержательное введение логарифмов, систематически отрабатывать алгебраические преобразования и прояснить смысл и свойства функции [15]. В университетском курсе полезно последовательно разъяснять и демонстрировать понятие предела (в том числе через контрпримеры), вводить явный «каталог» неопределенностей с диагностическими признаками выбора метода.
Таким образом, низкая успешность по «пределам» обусловлена не «новизной» определения, а неумением проводить алгебраические преобразования и слабым понимания понятия функции, необходимых для распознавания ситуации и обоснованного выбора метода.
Выводы
1. Причина провала на «пределах». Более низкая успешность по сравнению с «производными» обусловлена не «новизной» темы, а пробелами школьной базы: слабые алгебраические преобразования (в том числе логарифмы, рационализация) и фрагментарные представления о функции (ОДЗ, свойства, графики). Совпадение трех индикаторов – распределений, долей «≥ 3» с 95 % ДИ Уилсона и аппроксимационных средних – подтверждает вывод и согласуется с идеями о разрыве между образом понятия и ε–δ-определением, а также с типичными метафорами/ошибками распознавания предельных ситуаций.
2. Представляется, что в школе необходимы раннее и содержательное введение логарифмов, системная проработка по теме «Алгебраические преобразования», тщательное разъяснение понятия функции, а в вузах нужно обратить внимание на поэтапное введение понятия предела и его концептуальное разъяснение.
3. Практическая значимость исследования состоит в том, что предложенные меры делают более плавным переход от школьного курса к университетскому математическому анализу.



