Введение
На современном этапе достижение нового качества образования связывают с процессом его цифровизации и активным использованием дистанционных образовательных технологий. При этом основная роль отводится общеобразовательной школе, которая должна быть ориентирована не только на усвоение обучающимся определенной суммы знаний, но и на развитие его личности, познавательных способностей [1]. Геометрия является одной из важнейших дисциплин, развивающих интуитивные, логические, пространственные, конструктивные компоненты умственной деятельности обучающихся, в связи с чем эффективное методическое сопровождение процесса обучения геометрии выступает одной из ключевых задач повышения уровня математического образования школьников [2, с. 237].
Стремительное развитие дистанционных образовательных технологий (ДОТ) обусловлено совокупностью педагогических, социальных и технологических факторов: недостаточной гибкостью традиционных фронтальных форм преподавания, препятствующих индивидуализации обучения; потребностью в образовательной инклюзии для обучающихся с ограниченными возможностями здоровья либо проживающих в отдаленных регионах; нехваткой квалифицированных педагогических кадров в ряде субъектов Российской Федерации, в сельских школах, в малокомплектных образовательных учреждениях. По мнению исследователей, внедрение ДОТ в образовательную среду школы может способствовать решению обозначенных проблем за счет адаптации учебного процесса к индивидуальным образовательным потребностям школьников, обеспечения равного доступа к высококачественным образовательным продуктам [3]. Сказанное позволяет рассматривать дистанционное обучение как методическую инновацию, которая ввиду открытости, гибкости и эвристичности выступает в разных моделях взаимодействия с традиционной системой обучения, поддерживая и развивая ее потенциал.
В то же время следует констатировать, что методические основы применения дистанционных образовательных технологий остаются все еще недостаточно проработанными. В частности, как отмечает В.И. Снегурова, не хватает фундаментальных практических исследований по теории и практике дистанционного обучения в системе общего образования; явно выражена тенденция «механического переноса» методов, форм и средств традиционного очного обучения в дистанционный формат; отсутствуют методические рекомендации для сетевых учителей по организации дистанционного обучения математике, а также четко определенные механизмы диагностики его эффективности [4, с. 6]. В этой связи актуализируется необходимость научного поиска, направленного на проектирование модели методического сопровождения обучения математическим дисциплинам в дистанционном формате и разработку технологии такого сопровождения в массовой практике.
Цель исследования – теоретическое обоснование и практическая реализация методического сопровождения дистанционного факультативного курса по геометрии для обучающихся старших классов общеобразовательной школы.
Задачи исследования:
1) анализ современного состояния дистанционного обучения геометрии в общеобразовательной школе;
2) построение модели методического сопровождения дистанционного обучения старшеклассников геометрии;
3) разработка технологии качественного интерактивного взаимодействия субъектов образовательного процесса и экспериментальная проверка ее эффективности.
Материалы и методы исследования
Для достижения цели и решения задач исследования использовался комплекс методов: теоретические (анализ психолого-педагогической и методической литературы; анализ федеральных государственных образовательных стандартов, рабочих программ по математике для общеобразовательных школ, учебных пособий и дидактических материалов; анализ, синтез, обобщение, моделирование) и эмпирические (обобщение методического опыта преподавания математических дисциплин в общеобразовательной школе, наблюдение, педагогический эксперимент).
Результаты исследования и их обсуждение
Дистанционное обучение трактуется как процесс целенаправленного и методически организованного обучения с применением преимущественно средств информационных и коммуникативных технологий (ИКТ), при котором преподаватель и обучаемые разделены во времени и пространстве [5]. Модели дистанционного обучения весьма разнообразны и могут быть классифицированы по типу взаимодействия между субъектами образовательного процесса и объектами цифровой образовательной среды. Чем больший вес в образовательной модели имеют дистанционные технологии, тем более выражена специфика информационно-образовательной среды в сравнении с традиционным очным форматом обучения.
Можно выделить следующие направления трансформации компонентов методической системы, в которую интегрированы ДОТ: 1) изменение способа постановки целей обучения (от общей цели для всего класса к индивидуальной цели для каждого обучающегося, скорректированной с учетом его индивидуальных особенностей, интересов, уровня обученности, темпа освоения материала); 2) изменение подхода к структурированию учебного содержания (дифференциация образовательного контента, модульный принцип его построения, выделение инвариантной и вариативной составляющих); 3) разнообразие форматов взаимодействия обучающихся и педагогов (синхронный – онлайн-уроки, вебинары, консультации, интерактивные семинары; асинхронный – просмотр обучающих материалов, выполнение заданий в LMS, участие в форумах; групповая деятельность – сетевые исследовательские проекты, коллективные презентации, кейс-стади); 4) расширение арсенала средств обучения (виртуальные лаборатории, онлайн-тренажеры, интерактивные рабочие листы и т.д.) и средств оценивания образовательных результатов (цифровые портфолио с индивидуальными результатами проектных работ, адаптивное тестирование с автоматической настройкой сложности заданий и т.п.); 5) изменение организационных форм и методов обучения (от традиционного урока – к формату «перевернутого» класса, от традиционного диалога учителя и ученика – к опосредованному интерактивному общению в электронной информационно-образовательной среде, от объяснительно-иллюстративных методик – к значительному увеличению доли самостоятельной, проектной и исследовательской деятельности).
Обозначенная специфика процесса обучения с применением ДОТ требует от современного учителя математики наличия широкого спектра компетенций в области организации взаимодействия субъектов учебной деятельности: знания принципов отбора и структурирования математического содержания, предназначенного для освоения в дистанционном формате; умения выбирать наиболее эффективные формы проведения занятий в синхронном и асинхронном режимах; способности выстраивать взаимодействие в сети и поддерживать мотивацию обучающихся в условиях их пространственной разобщенности. Вследствие этого актуальной задачей выступает разработка методического сопровождения, направленного на оказание помощи педагогу в организации дистанционного обучения математическим дисциплинам.
Под методическим сопровождением дистанционного обучения геометрии понимаем непрерывный процесс поддержки участников образовательного процесса, направленный на организацию и упорядочение их деятельности в открытой информационной среде на основе интеграции комплекса методов, форм и средств традиционного и дистанционного обучения. Такая поддержка подразумевает обеспечение педагогов методическими ресурсами, сценариями дистанционных уроков, консультирование по вопросам их интеграции в учебный процесс, помощь в разработке разноуровневых заданий к индивидуальным и групповым занятиям, в организации диагностики достижения образовательных результатов.
В научно-педагогической литературе представлен достаточно широкий спектр исследований, посвященных теоретическим основам разработки методического обеспечения образовательного процесса с применением ДОТ. В частности, Е.Г. Гаевской охарактеризованы дидактические требования к образовательной среде, диктуемые особенностями ее цифровизации, раскрыты методические аспекты реализации междисциплинарного подхода и проектного метода при переходе от офлайн-обучения к онлайн-обучению [6]. С.И. Белозеровой, О.И. Чуйко проанализированы возможности, достоинства и недостатки LMS Moodle, описан процесс создания и сопровождения дистанционных учебных курсов, приведены рекомендации по их структуре и наполнению учебно-методическими материалами [7]. Т.С. Шириковой описана методика поэтапного формирования умений, связанных с проведением доказательства теорем, обеспечивающая интеграцию в учебном процессе содержания субъектного опыта учащихся с опытом осуществления компьютерного эксперимента [8]. Исследование И.Н. Макарьева посвящено построению системы методического сопровождения дистанционного обучения старшеклассников математике, ключевой особенностью которой выступает фундирование образовательного контента концепцией социокультурного содержания математического образования и теорией поэтапного формирования умственных действий [9].
Отличительной особенностью модели методического сопровождения обучения геометрии, представленной в настоящем исследовании, является ее ориентация на развивающую цель организации учебной деятельности с применением ДОТ: базисный вектор сопровождения направлен на создание интерактивной исследовательской среды, в которой у школьников будут развиваться ключевые компоненты математического мышления, повышаться уровень внутренней мотивации к учению и, как следствие, степень продуктивности познавательной деятельности.
Методологический блок модели составляют теории развития личности (A.B. Асмолов [10]), теории развития мышления (Л.В. Воронина, Л.И. Миронова и др. [11]), исследования по проблеме формирования математических понятий (М.А. Холодная, Э.Г. Гельфман [12]). Фундаментальной основой данных исследований выступает системно-деятельностный подход к изучению закономерностей развития сознания и личности, согласно которому именно деятельность как форма активного, преобразующего отношения к действительности признается ключевым фактором формирования психических структур и базовых интеллектуальных способностей. Системно-деятельностный подход реализуется в русле проводимого исследования в виде технологии организации учебно-исследовательской деятельности старшеклассников по решению систематизированного комплекса геометрических задач в среде динамической геометрии в рамках дистанционного факультативного курса.
К методологическим основаниям исследования также следует отнести широкий пласт научных работ, посвященных изучению мыслительного процесса и выявлению его специфики при решении математических задач. По мнению Л.С. Капкаевой [13], И.А. Бреус [14], В.А. Тестова [15], своеобразие математического мышления выражается в аналитико-синтетической направленности схемы рассуждений, в преобладании дедуктивного метода, в оперировании цифровой и знаковой символикой, в умении ориентироваться в пространстве и создавать различные комбинации геометрических образов. Другими словами, особенность математического мышления заключается в сочетании строгой логики и наглядных представлений, аксиоматической и конструктивной процедур, рационального и образно-ассоциативного компонентов. Это позволяет рассматривать логический и пространственный компоненты в качестве базовых составляющих мыслительной деятельности школьников при освоении математического содержания (рис. 1).
Целевой блок модели включает личностно-ориентированную цель обучения геометрии с применением ДОТ, выражающуюся в повышении качества математической подготовки школьников, и сопряженные с нею задачи: мотивационно-стимулирующую (развитие познавательного интереса посредством включения обучающихся в деятельность по исследованию моделей геометрических фигур); обучающую (закрепление, углубление, систематизация предметных знаний); развивающую (развитие логического и пространственного компонентов мышления на основе взаимодополнительности аналитического и синтетического метода представления геометрического содержания).
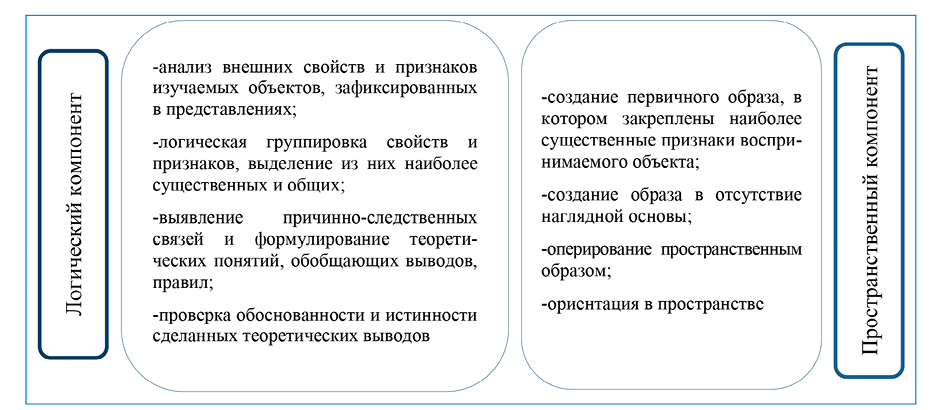
Рис. 1. Структура логического и пространственного компонентов мыслительной деятельности Примечание: составлен авторами
Общая концепция содержательного блока модели ориентирована на расширение существующей методики преподавания за счет применения цифровых технологий. В качестве геометрического содержания, на котором осуществляется развитие компонентов мыслительной деятельности школьников, выступают задачи на построение, составляющие одну из традиционных тематических линий основного курса геометрии. Богатство дидактического потенциала этих задач в плане развития математического мышления обусловлено необходимостью обращения в процессе их решения к широкому спектру геометрических фигур, выполнения анализа существенных отношений и установления логических связей, выдвижения гипотезы и составления плана ее проверки, проведения разнообразных конструктивных преобразований (движение, наложение, симметричное отражение и т.п.), выстраивания доказательства соответствия полученного результата требованиям задачи. Таким образом, в процессе деятельности школьников по решению задач на построение актуализируются операции, входящие в состав как логического, так и пространственного компонентов мышления.
Обобщение методического опыта преподавания математических дисциплин в общеобразовательной школе указывает на имеющиеся существенные трудности в освоении школьниками методов решения задач на построение, выражающиеся в неумении мысленно представлять фигуры, их пересечения и преобразования; в формальном знании аксиом построения и слабом навыке их применения; в сложности проведения анализа, доказательства и исследования. Во многом перечисленные трудности обусловлены несовершенством существующей методики обучения решению задач данного типа: выраженным дефицитом времени, формальным подходом к заучиванию готовых алгоритмов, несистемным характером изложения без акцента на отработку ключевых методов решения. Действенным инструментом преодоления сложившейся ситуации выступают компьютерные системы динамической геометрии (СДГ).
Информационно-технологический блок модели методического сопровождения обучения геометрии представлен системой динамической геометрии GeoGebra, предоставляющей широкий функционал операций, идентичных операциям на построение, инструменты для создания 3D-визуализаций, а также возможность использования на мобильных устройствах и в облачных сервисах [16]. Наиболее значимым преимуществом СДГ GeoGebra в рамках данного исследования выступает реализация когнитивно-визуального подхода, основанного на идее рационального совмещения невербального (образного) и понятийного (логического) компонентов мышления в учебном познании [17].
Процессуальный блок модели методического сопровождения обучения геометрии обеспечивает дидактическое взаимодействие педагога и обучающихся в цифровой образовательной среде с применением ДОТ. Выделены следующие этапы организации учебной деятельности старшеклассников по освоению методов решения задач на построение: мотивационно-подготовительный этап (вовлечение в дистанционный формат обучения, входная диагностика, постановка общих и индивидуальных образовательных целей); этап асинхронного взаимодействия (освоение базовой составляющей геометрического содержания в рамках индивидуальной образовательной траектории); этап синхронного взаимодействия (углубленное освоение геометрического содержания в процессе интерактивного общения участников образовательного процесса); контрольно-диагностический этап (осуществление выходного контроля и самоконтроля, групповой либо индивидуальной рефлексии). Перечисленные этапы реализуются в рамках дистанционного факультативного курса «Решение задач на построение в интерактивной геометрической среде», предназначенного для обучающихся 10–11-х классов общеобразовательной школы (табл. 1).
К каждому занятию курса разработан методический кейс, включающий: видеоинструкцию по работе с инструментами СДГ GeoGebra; теоретический блок, содержащий сведения о геометрических фигурах и их свойствах, справочно-биографические материалы; шаблоны для демонстрации методов решения задач на построение; подборку разноуровневых тренировочных заданий для организации индивидуальной работы; комплекс задач для решения в формате интерактивного группового взаимодействия; задания для входной и выходной диагностики.
Оценочно-диагностический блок модели обеспечивает систематический мониторинг уровня развития компонентов мыслительной деятельности школьников при освоении геометрического содержания на основе комплекса критериев и соответствующих им локальных показателей (табл. 2). В ходе исследования разработаны диагностические задания, ориентированные на оценку результативности интеграции дистанционных образовательных технологий в процесс обучения геометрии.
Таблица 1
Тематическое планирование дистанционного факультативного курса «Решение задач на построение в интерактивной геометрической среде»
|
№ |
Тема занятия |
Краткое содержание |
Часы |
|
1 |
Общие аксиомы конструктивной геометрии |
Основные фигуры геометрии. Понятие задачи на построение. Постулаты построений с помощью циркуля и линейки |
2 |
|
2 |
Элементарные построения циркулем и линейкой |
«Опорные» геометрические задачи на построение |
4 |
|
3 |
Схема решения задач на построение |
I. Анализ. II. Построение. III. Доказательство. IV. Исследование |
2 |
|
4 |
Метод пересечений |
Построение дуги, вмещающей данный угол. Окружность Аполлония |
2 |
|
5 |
Метод движений |
Решение задач на построение методом параллельного переноса. Вращение. Образ точки. Образ прямой |
4 |
|
6 |
Метод подобия |
Гомотетия. Образ точек при гомотетии. Решение задач на построение методом подобия |
4 |
|
7 |
Метод симметрии |
Задача Герона. Задача Фаньяно. Задача Ферма – Торричелли – Штейнера |
4 |
|
8 |
Метод инверсии |
Инверсия. Окружность инверсии. Центр инверсии. Степень инверсии. Свойства инверсии |
4 |
|
9 |
Алгебраический метод |
Построение отрезков, заданных формулами |
2 |
|
10 |
Задачи на построение, не разрешимые циркулем и линейкой |
Признак разрешимости задач на построение циркулем и линейкой. Задача о трисекции угла. Задача об удвоении куба. Задача о спрямлении окружности. Задача о квадратуре круга. Построение правильных многоугольников |
6 |
|
Итого |
34 ч |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
Таблица 2
Уровни сформированности компонентов мыслительной деятельности школьников при решении задач в системе динамической геометрии
|
Уровни |
Критерии сформированности компонентов мыслительной деятельности |
Показатели умений при решении геометрических задач |
|
Низкий |
– эпизодический характер проявления познавательной активности, – предпочтение задачам, решаемым по готовым шаблонам и образцам, – отсутствие критического анализа идей и выводов, – инертность мышления, неспособность выйти за пределы заданного способа действия |
– умение выявлять структуру задачи (данные, искомые, свойства и отношения), – умение сопоставлять данную задачу с известными классами задач с целью отыскания идеи решения, – умение составлять план решения, – умение создавать статичные пространственные образы, |
|
Средний |
– устойчивая познавательная активность, – осуществление переноса знаний и умений в новую ситуацию, – осознанное стремление к оценке результатов своей деятельности с целью ее дальнейшего усовершенствования |
– умение выявлять существенные отношения в системе данных задачи, – умение ставить цель и произвольно выстраивать программу умственных действий, – умение осуществлять пошаговый самоконтроль и коррекцию мыслительного поиска, – умение оперировать пространственными образами |
|
Высокий |
– интерес к причинно-следственным связям, к выявлению закономерностей, – способность гибко реагировать на меняющуюся ситуацию, отыскивая новые средства ее решения, – объективное осмысление своих действий с точки зрения достижения оптимального способа решения задачи |
– умение самостоятельно комбинировать известные способы деятельности в новый, – умение исследовать частные случаи решения, – умение комбинировать пространственные образы |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
Раскроем технологические аспекты функционирования представленной модели методического сопровождения обучения старшеклассников геометрии на каждом из этапов организации учебной деятельности в рамках дистанционного факультативного курса.
Для проведения дистанционных занятий используется виртуальная доска Padlet, предоставляющая возможность размещения контента разных типов и создания онлайн-уроков любой предметной направленности.
Мотивационно-подготовительный этап занятия направлен на развитие у школьников положительной мотивации к изучению геометрии. Как известно, познавательная мотивация выступает основным источником активности личности, обеспечивая перевод объективно значимой цели учения в личностно значимую, субъективно принятую [18]. Пробуждение потребности в овладении геометрическими знаниями и формирование на ее основе познавательного мотива обеспечивается такими методическими приемами, как обращение к биографическим материалам, привлечение исторических сведений о геометрических объектах, решение задач с практическим содержанием, демонстрация преимуществ интерактивной геометрической среды для визуализации исследуемых фигур. Мотивационные задачи подбираются для каждого занятия курса и размещаются на доске Padlet в формате коротких видеороликов для предварительного просмотра обучающимися.
Пример 1. Задача Ферма – Торричелли – Штейнера: «На плоскости даны три точки A, B, C, не лежащие на одной прямой. Для какой точки T плоскости сумма расстояний AT + BT + CT наименьшая?»
История этой задачи, помещенной в книге итальянского физика Винченто Вивиани «О максимальных и минимальных значениях» в 1659 г., насчитывает более трех с половиной столетий. Еще до книги Вивиани этой задачей интересовался итальянский математик и физик Эванджелиста Торричелли (1608–1647), считается, что именно он получил первое решение, основанное на физических соображениях. Согласно другим источникам, независимо от Торричелли эту задачу решил величайший французский математик Пьер Ферма (1601–1665), а первое чисто геометрическое решение принадлежит швейцарскому геометру Якобу Штейнеру (1796–1863).
Пример 2. Знаменитая задача об отражении света впервые была решена древнегреческим математиком Героном Александрийским (I в. н.э.) в трактате «О зеркалах» (рис. 2). В традиционной постановке она формулируется как задача поиска кратчайшего пути между двумя точками с заходом на прямую, однако ей легко дать практическую интерпретацию: в какой точке на прямой дороге нужно поставить автобусную остановку, чтобы суммарный путь до нее от городов A и B был наименьшим?
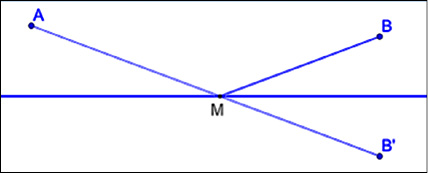
Рис. 2. Решение задачи с практическим содержанием Примечание: составлен авторами
Важным моментом мотивационно-подготовительного этапа является проведение входной диагностики для последующей постановки образовательных целей. Перед изучением каждой темы педагог устанавливает, в какой степени учащиеся владеют опорными понятиями, необходимыми для освоения нового знания, и в какой мере у них сформированы умения решать простейшие («опорные») задачи на построение, служащие составными шагами в решении более сложных задач.
Так, при изучении метода пересечений новой для школьников дефиницией является «дуга, вмещающая данный угол». Для успешного ее освоения обучающиеся должны прочно владеть такими базовыми понятиями, как окружность, радиус, хорда, дуга, центральный угол.
Входная диагностическая работа включает следующий блок заданий:
1) На данном рисунке найдите все центральные углы и все дуги, на которые эти углы опираются.
2) На данном изображении окружности с центром в точке O и несколькими точками на ней (A, B, C, D) определите сумму градусных мер дуг AB и BC. Если дуга AC равна 180°, то может ли дуга AB быть равной 100°? Ответ поясните.
3) Постройте биссектрису данного неразвернутого угла.
4) Постройте прямоугольный треугольник по гипотенузе и острому углу.
5) Постройте касательную к окружности, проходящую через данную на ней точку.
Задания диагностической работы размещаются на доске Padlet, а их решение осуществляется на виртуальной платформе GeoGebra Classroom. Старшеклассники выполняют задания самостоятельно и направляют учителю ссылку на полученный результат. В свою очередь, педагог оценивает степень готовности обучающихся к изучению новой темы и размещает на доске Padlet общую образовательную цель (для всего класса): овладеть понятием «дуга, вмещающая данный угол» и умением применять знания о вписанных и центральных углах при решении широкого круга задач на построение.
Этап асинхронного взаимодействия направлен на актуализацию знаний и освоение базовой составляющей геометрического содержания по каждой теме курса. Обучающиеся самостоятельно изучают размещенные в пространстве Padlet теоретические сведения о геометрических фигурах, просматривают подготовленный педагогом скринкаст с объяснением решения опорных задач на построение. В качестве примера на рис. 3 приведен фрагмент теоретического блока к занятию по теме «Дуга, вмещающая данный угол».
Далее школьники самостоятельно выполняют серию тренировочных заданий по изучаемой теме. При этом на основе результатов входной диагностики осуществляется индивидуализация образовательной траектории:
− обучающимся с низким уровнем подготовки (не усвоившим базовые понятия) предлагаются корректирующие задания – работа на готовом чертеже («На рисунке найдите все вписанные углы, опирающиеся на дугу AC»), применение теории в простейшей ситуации («Найдите величину вписанного угла, если соответствующий ему центральный угол равен 80°»);
− обучающимся со средним уровнем подготовки (усвоившим базовые понятия, но не умеющим применять их в нестандартных условиях) предлагается серия поддерживающих заданий – на поиск несоответствий («Два вписанных угла, опирающиеся на одну и ту же дугу, равны 35° и 40°. Возможна ли такая ситуация? Объясните ответ»), на установление связей между базовыми понятиями («Найдите угол между хордами, если он равен полусумме дуг»), на применение знаний о свойствах геометрических фигур («В окружность вписан треугольник ABC. Угол A равен 50°, дуга BC равна 100°. Найдите углы B и C, используя как теорему о вписанном угле, так и теорему о сумме углов треугольника»);
− обучающимся с высоким уровнем подготовки (легко справившимся с диагностической работой) выдаются задания, требующие широкого применения теории (нахождение отношений отрезков, доказательство перпендикулярности или параллельности прямых, построение треугольника по заданным его элементам).
Этап синхронного взаимодействия предполагает освоение геометрического содержания на углубленном уровне в процессе интерактивного общения педагога и обучающихся. Помимо доски Padlet и платформы GeoGebra Classroom, используются инструменты видеоконференцсвязи (Zoom, Яндекс Телемост, SaluteJazz и т.п.).
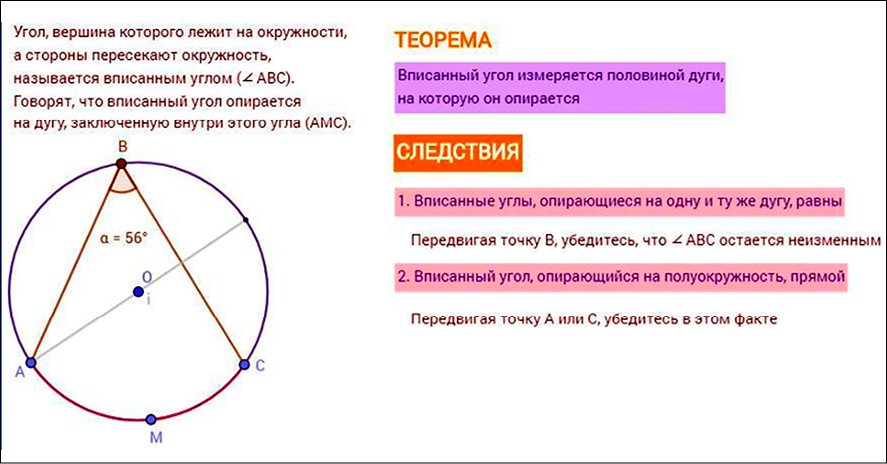
Рис. 3. Теоретический блок для освоения понятия «дуга, вмещающая данный угол» Примечание: составлен авторами на основе источника [19]
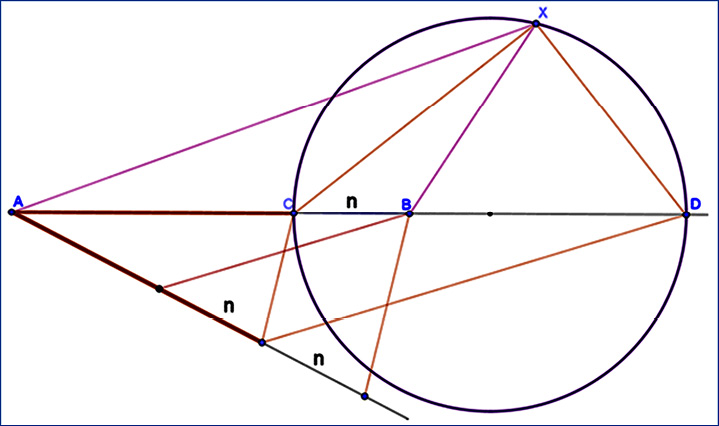
Рис. 4. Окружность Аполлония Примечание: составлен авторами
Таблица 3
Комплекс диагностических заданий для оценки уровня сформированности компонентов мыслительной деятельности школьников
|
Уровень |
Диагностируемые умения |
Характеристика и пример задания |
|
Низкий |
– выявлять структуру задачи (данные, искомые, свойства и отношения), – сопоставлять данную задачу с известными классами задач с целью отыскания идеи решения, – составлять план решения, – создавать статичные пространственные образы |
Задание репродуктивного типа. Рассчитано на применение некоторого известного алгоритма на базе изученных теоретических положений и усвоенных практических приемов деятельности. «Дан параллелограмм ABCD, у которого AB=1, BC=2, а угол ABC является тупым. Через каждую из точек B и D проведены две прямые, одна из которых перпендикулярна стороне AB, а другая – стороне BC. В пресечении этих прямых получился параллелограмм, подобный параллелограмму ABCD. Найти площадь параллелограмма ABCD». Для решения требуется создать динамическую модель, приводящую к уравнению
|
|
Средний |
– умение выявлять существенные отношения в системе данных задачи, – умение ставить цель и произвольно выстраивать программу умственных действий, – умение осуществлять пошаговый самоконтроль и коррекцию мыслительного поиска, – умение оперировать пространственными образами |
Задание реконструктивно-вариативного типа. Требует выявления некоторых скрытых связей между фигурами и их элементами, применения изученных теоретических положений в новых условиях, перестройки известных способов решения. «Около треугольника ABC описана окружность с центром O, угол AOC равен 60°. В треугольник ABC вписана окружность с центром M. Найти угол AMC». Необходимо построить окружность с центральным углом AOC = 60°. Точка В отмечается на окружности произвольно. После этого в треугольник ABC вписывается окружность с центром в точке M и измеряется угол AMC. Динамическая модель позволяет выяснить, что полученный результат верен только при условии, когда точки M и O находятся по разные стороны от хорды AC. В противном случае ответом к задаче будет служить величина угла, дополнительного к углу AMC.
|
|
Высокий |
– умение самостоятельно комбинировать известные способы деятельности в новый, – умение исследовать частные случаи решения, – умение комбинировать пространственные образы |
Задание продуктивно-творческого типа. Предполагает открытие «новых» свойств фигур или их взаимосвязей, выявление причинно-следственных связей, закономерностей, комбинирование новых способов деятельности из известных. «Найти на плоскости геометрическое место точек, сумма расстояний от которых до прямых, содержащих стороны равностороннего треугольника, является постоянной». Для решения необходимо построить динамическую модель, позволяющую изменять положение точки X, и использовать в ней динамический текст, благодаря которому можно будет следить за тем, как изменяется сумма длин перпендикуляров, проведенных из точки X к прямым, содержащим стороны данного треугольника (AC, CB, AB). Такой эксперимент дает возможность сформулировать гипотезу о том, что значения суммы длин перпендикуляров постоянны для любых точек, лежащих внутри данного треугольника или на его границе. Для проверки гипотезы необходимо создать другую динамическую модель, в которой точка X ограничена областью треугольника (использовать инструмент «точка на объекте»).
|
Примечание: составлена авторами на основе полученных данных в ходе исследования
На данном этапе преимущество отдается поисковому и проблемному методам обучения, предполагающим организацию активной, поэтапно контролируемой и направляемой преподавателем совместной работы класса по поиску подходов к решению поставленных задач. При этом широко задействуются иллюстративные возможности СДГ GeoGebra как инструмента динамического моделирования и ее функционал.
На рис. 4 представлена задача на построение в СДГ GeoGebra, в ходе решения которой применяется поисковый метод: «Дан отрезок AB и точка C, принадлежащая прямой AB. Построить геометрическое место точек F = {X|AX:XB=AC:CB} (окружность Аполлония)». На этапе анализа, предположив, что задача решена, обозначим за Х одну из точек искомого множества F. Очевидно, ХС является биссектрисой угла АХВ. Взяв точку D на прямой АВ, такую, что ХD перпендикулярна ХС, делаем вывод, что ХD – биссектриса угла, внешнего для АХВ. Следовательно, ∠CXD прямой и точка Х лежит на окружности диаметра CD. Проводя обратные рассуждения, доказываем, что любая точка окружности с диаметром CD принадлежит множеству F – окружности Аполлония. Рассуждая методом восходящего анализа, получаем алгоритм: чтобы построить окружность Аполлония, достаточно найти точку D и провести окружность с диаметром CD.
Контрольно-диагностический этап предполагает организацию выходного контроля степени освоения геометрического содержания и сформированности компонентов математического мышления. Диагностика проводится на основе комплекса задач, структурированных с учетом усложнения алгоритмов и повышения степени логической строгости решения, меры обобщенности создаваемых геометрических образов (табл. 3).
Опытно-экспериментальная работа по апробации методического сопровождения обучения геометрии осуществлялась в 2024–2025 учебном году на базе ФГБОУ «Елецкий государственный университет им. И.А. Бунина». В рамках деятельности инновационной образовательной площадки «Развитие интеллектуальной мобильности обучающихся в цифровой образовательной среде университета» преподавателями кафедры математики, информатики, физики и методики обучения проводились занятия факультативного курса «Решение задач на построение в интерактивной геометрической среде» для школьников, посещающих университетский класс «Суббота с УНИВЕРом». Экспериментальная группа включала 50 обучающихся 10-х классов физико-математического профиля общеобразовательных учреждений г. Ельца.
Для определения эффективности методического сопровождения обучения геометрии в аспекте мотивационной составляющей познавательной деятельности школьников использовалась методика диагностики направленности учебной мотивации Т.Д. Дубовицкой [20]. Измерения производились до и после изучения факультативного курса. Старшеклассники выражали свое отношение к занятиям, заполняя анкету с оценочными суждениями по шкале «верно», «скорее верно», «скорее неверно», «неверно». Примеры суждений: «Мне неинтересно решать задачи на построение, посещаю факультативные занятия по просьбе родителей», «Посещаю занятия только для того, чтобы общаться с друзьями», «Мне интересно больше узнать о конструктивной геометрии и интерактивных геометрических системах», «Испытываю желание сделать новое математическое открытие», «Хочу участвовать в математических конкурсах и олимпиадах» и др.
В зависимости от суммы набранных баллов (максимальное количество – 20) обучающиеся были разделены на группы по уровню направленности учебной мотивации: низкий (0–5 баллов) – не проявляет интерес к учебной деятельности, внутренние мотивы подчинены внешним; средний (6–14 баллов) – образовательная цель личностно принята, внешние и внутренние мотивы сбалансированы; высокий (15–20 баллов) – легко включается в деятельность, демонстрируя осознание ее смысла, внутренние мотивы носят доминирующий характер (табл. 4). До экспериментального обучения выборочная средняя и стандартное отклонение составили х = 10,56; σ = 4,87, после обучения х = 13,75; σ = 2,47 соответственно. Проверка с применением t-критерия Стьюдента для зависимых выборок на уровне значимости α = 0,05 выявила, что tэмп = 4,14 > tкр(0,05; 48) = 2,011. Таким образом, установлено значимое различие в уровне направленности учебной мотивации старшеклассников до и после дистанционного обучения с применением системы динамической геометрии.
Для определения эффективности методического сопровождения обучения геометрии в аспекте развития мыслительной деятельности обучающихся после завершения факультативного курса приводилась диагностическая контрольная работа (табл. 4).
Таблица 4
Результаты проведения опытно-экспериментальной работы
|
Распределение обучающихся по уровням направленности учебной мотивации |
Распределение обучающихся по уровням сформированности компонентов мыслительной деятельности |
||||
|
Уровни |
До, % |
После, % |
Уровни |
До, % |
После, % |
|
Низкий |
42 |
20 |
Низкий |
38 |
18 |
|
Средний |
52 |
69 |
Средний |
54 |
70 |
|
Высокий |
6 |
11 |
Высокий |
8 |
12 |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
Проверялась нулевая гипотеза: H0 − различий между эмпирическими распределениями (уровнем сформированности компонентов мыслительной деятельности до и после экспериментального обучения) нет. Альтернативная гипотеза H1 − различия между двумя эмпирическими распределениями не случайны. Эмпирическое значение критерия tэмп = 3,63 больше критического tкр (0,05; 48) = 2,011 на уровне значимости α = 0,05, следовательно, расхождения между распределениями статистически значимы.
Заключение
Проведенное исследование показало, что при соблюдении методических и организационных условий дистанционные образовательные технологии обладают существенным потенциалом в аспекте развития мыслительной деятельности и познавательной активности обучающихся. Разработанная модель методического сопровождения обучения геометрии позволяет выстроить эффективный формат дистанционного взаимодействия педагога и обучающихся, способствующий не только усвоению предметных знаний, но и развитию компонентов интеллектуальной сферы школьников. В то же время успешная реализация представленной технологии требует от учителя математики готовности к постоянному профессиональному росту и освоению роли тьютора-навигатора в цифровой образовательной среде.




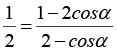 , α – угол
, α – угол 



