Введение
Оценка пожаровзрывоопасных материалов (ПВОМ) по их чувствительности и опасности, необходимая для решения вопросов лабораторной, технологической и эксплуатационной безопасности [1; 2, с. 108–134; 3, с. 250–273]. Она базируется на установлении аналогичности свойств и условий превращений ПВОМ со свойствами и условиями превращения ПВОМ из опорного (или практического) ряда чувствительности и опасности [4–6]. Практическая важность сравнительного анализа заключается в возможности установлении мер сходства и отличий ПВОМ по набору свойств материалов, в том числе качественных, их аналогичности или близости с определенными мерами в многомерном пространстве признаков и построении на их основе рядов чувствительности и опасности [1; 5; 6]. Однако в стандартизованной практике оценки чувствительности и опасности ПВОМ отсутствует формализованный алгоритм анализа многомерных данных [3, с. 275–280; 5]. Одним из следствий этого является несоответствие опорному ряду искусственных рядов чувствительности и опасности, построенных с использованием частных или усредненных критериев чувствительности ПВОМ [2, с. 87–95; 3, с. 90–99; 4].
С другой стороны, к настоящему времени разработаны математические методы [7, с. 130–149; 8; 9], алгоритмы и комплексы программ анализа, классификации, группировки, ранжирования многомерных данных. Данные методы показывают высокую эффективность для обработки данных различного типа [10, с. 113–120; 11, с. 474; 12, с. 180–200]. Среди этих методов, учитывая природу физико-химических свойств ПВОМ и задач по обеспечению безопасности работ с этим классом материалов, следует акцентировать внимание на методах кластерного анализа [6; 7, с. 37–52; 9]. Судя по большому объему публикаций и пакетов прикладных программ, кластерный анализ применяется на протяжении десятков лет в смежных областях знаний и технологической практике, однако практически не используется при решении вопросов оценки чувствительности и опасности ПВОМ. В кластерном анализе группировка объектов по совокупности свойств-признаков, установление их близости и аналогичности проводится на основе различных мер и шкал с построением наглядных дендрограмм объединения объектов в кластеры [7, с. 65–70; 9; 11, с. 378–385]. В качестве базовой меры близости объектов в большинстве методов кластерного анализа используется евклидово расстояние S = djk между j-м и k-м объектами совокупности [7]:
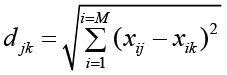 ,
,
где М – количество признаков-свойств; j, k – номера объектов, j, k = 1…N; N – общее количество выбранных для анализа объектов. В качестве начального центра для расчета расстояний и группировки данных может использоваться любой объект, что позволяет строить ряды объектов по возрастанию или убыванию меры близости между объектами или кластерами. В качестве критерия объединения объектов в группы служит достаточно общее требование – расстояние между объектами в группе должно быть меньше расстояния между группами. При этом анализ сопровождается дополнительными статистическими оценками. Методы, алгоритмы обработки данных с использованием кластерного анализа детально рассмотрены в многочисленных публикациях и реализованы в большом количестве доступных пакетов программ, например Deductor, Minitab, Statistica, SPSS и др., включающих обширный арсенал других статистических методов анализа данных [7, с. 96–108; 12, с. 160–170.
В настоящей статье представлены результаты, показывающие целесообразность и эффективность применения кластерного анализа для решения задач статистического анализа и группировки объектов из выборки данных по термическому разложению и тепловому взрыву достаточно широкой группы ПВОМ – индивидуальных энергетических соединений (вторичных и инициирующих взрывчатых веществ – ВВ) [5; 10, с. 187–194; 13].
Цель исследования – классификация, сравнительный анализ, построение опорных рядов чувствительности и опасности групп пожаровзрывоопасных материалов с использованием кластерного анализа.
Материалы и методы исследования
В качестве объектов исследования для кластеризации выбрана широкая группа энергетических соединений разных классов и назначения: нитрамины, нитроэфиры, окислители, соединения солевой природы, азиды, триазолы, ароматические нитросоединения; инициирующие и вторичные ВВ – наполнители, пластификаторы и др.) [6; 10, с. 237–249; 13]. Энергетические соединения из класса вторичных ВВ [6; 10, с. 280; 13]: № 1 – 1,3,5-триамино-2,4,6-тринитробензол (ТАТБ); № 2 – тринитротолуол (ТНТ); № 3 – 3-нитро-1,2,4-триазол-5-он (NTO); № 4 – 1,3,5,7-тетранитро-1,3,5,7-тетраазациклооктан (НМХ), № 5 – циклотриметилентринитрамин (RDX), № 6 – гексанитрогексаазаизовюрцитан (HNIW); № 7 – 1,4,5,9-тетранитрозо-1,4,5,9-тетраазадекалин (ТНАД); № 8 – 1,9-диазидо-2,4,6,8-тетранитро-2,4,6,8-тетраазанонан (ДИАЗ-4); соли динитрамида: № 9 – N-гуанилмочевинная (ГМС, GUDN); № 10 – гуанидиниевая (ГС, GDN); № 11 – аммониевая (ADN); № 12 – пентаэритриттетранитрат (ТЭН, PETN); № 13 – динитразапентан (ДНП); № 14 – 1-этил-3-нитро-1,2,4-триазол (Э-3Н), № 15 – эвтектика (1 и 2)-этил-3-нитро-1,2,4-триазола (Э-3Н*); № 16 – бис(2-фтор-2,2-динитроэтил)формаль (БЭФ, FEFO); № 17 – N-бис-(β-нитроксиэтил)нитрамин (ДИНА); № 18 – нитроэтилэтилолнитротриазол (НЭЭНТ). № 19 – динитратдиэтиленгликоля (ДНДЭГ), № 20 – динитраттриэтиленгликоля (ДНТЭГ), № 21 –нитроглицерин (НГЦ), № 22 – триметилолэтантринитрат (TMETN); № 23 – 1,3-диазидо-2-нитро-2-азопропан (ДИАЗ-1); № 24 – нитроцеллюлоза (НЦ); № 25 – фуразан-1,2,3,4-тетразин-1,3-диоксид (FTDO).
В качестве характеристик (признаков) термической чувствительности перечисленных соединений использовались параметры термического разложения компонентов в условиях термоанализаторов (Mettler Toledo) при фиксированной скорости повышения температуры (10 К/мин) – дифференциальной сканирующей калориметрии (ДСК), дифференциального термического ДТА) и гравиметрического анализов (ТГА) [5; 6; 13]: температура (Т) начала экзотермического разложения Тн, температура максимума первого пика экзотермического разложения Тмах, температура Тк, соответствующая завершению первого пика экзотермического разложения. В условиях ТГА определялась относительная к начальной потеря массы образцом ΔМ(Тмах) при температуре Тмах. Параметры теплового взрыва компонентов характеризуются данными по значениям критической температуры Ткр, соответствующей времени задержки (tз) теплового взрыва tз ≈ 60 мин при фиксированном диаметре цилиндрических образцов 20 мм [6; 10, с. 167; 13]. Максимальная размерность матрицы объекты – свойства равна 25×6. Информация о группировке признаков на основе корреляционного анализа [13] не использовалась. При построении рядов чувствительности к термическим воздействиям (классификация) использовалась информация о самом низко чувствительном материале – эталоне (ТАТБ).
В более узкой группе соединений опорных рядов чувствительности к внешним воздействиям [1; 3, с. 116–129; 6], включающей инициирующие и вторичные ВВ, используются: № 1 – ТНТ; № 2 – тетрил; № 3 – тетразен; № 4 – RDX; № 5 – HMX; № 6 – ТЭН (PETN); № 7 – НГЦ; № 8 – тринитрорезорцинат свинца, ТНРС; № 9 – гремучая ртуть; № 10 – азид свинца, АС; в качестве признаков рассматриваются температура вспышки Твсп, оС; теплота взрыва Q, ккал/кг; нижний предел чувствительности к удару, Но, мм. Цель анализа этой группы соединений – классификация на инициирующие и вторичные ВВ, сравнение с опорным рядом чувствительности и опасности. В качестве эталона с низкой чувствительностью [1] используется ТНТ. Статистическая обработка данных и их визуальное представление проводилось с использованием доступных пакетов программ: Deductor, Minitab.
Результаты исследования и их обсуждение
Далее приводится выборка из большого объема наиболее важных и интересных результатов. На рисунке показана дендрограмма объединения объектов в три кластера с использованием нормированного евклидового расстояния: первый кластер включает 1 объект – № 1, ТАТБ; второй кластер включает 11 объектов – № 1, 3, 5–7, 13–16, в том числе объекты опорных рядов – ТНТ, НМХ, RDX; третий кластер включает остальные 13 объектов, в том числе объекты опорных рядов – ТЭН (PETN), НЦ, НГЦ. Процесс объединения объектов в группы начинается с объединения наиболее близких элементов, с минимальными расстояниями между ними. Устанавливая разные пороги по расстоянию объединения объектов (уровень отсечения), можно получать разное количество кластеров с разным содержанием элементов. Например, уровень отсечения 40 % позволяет однозначно выделить два новых кластера, включающих по одному объекту: № 3 – ТНТ и № 25 – FTDO, которые расположены далеко – по расстоянию объединения, от предыдущих кластеров. Уровень отсечения в 35 % приводит к определению нового кластера, включающего три объекта: № 11 – ADN, № 18 – НЭЭНТ, № 23 – ДИАЗ-1, менее термически устойчивые по рассматриваемым признакам, чем НГЦ [5], но более стойкие, чем FTDO [1; 6].
Более полный анализ результатов кластеризации целесообразно проводить с использованием матрицы евклидовых расстояний (или других мер [7, с. 117]) между объектами. В качестве примера в табл. 1 приведена «усеченная» матрица (симметричная или инвариантная к транспонированию относительно главной диагонали) евклидовых расстояний между объектами в естественных переменных. Отсчет расстояний от диагональных элементов матрицы расстояний позволяет строить ряды объектов от любого объекта – соединения, выбранного в качестве первого члена ряда (эталона) – по значениям расстояний в соответствующем столбце или строке матрицы.
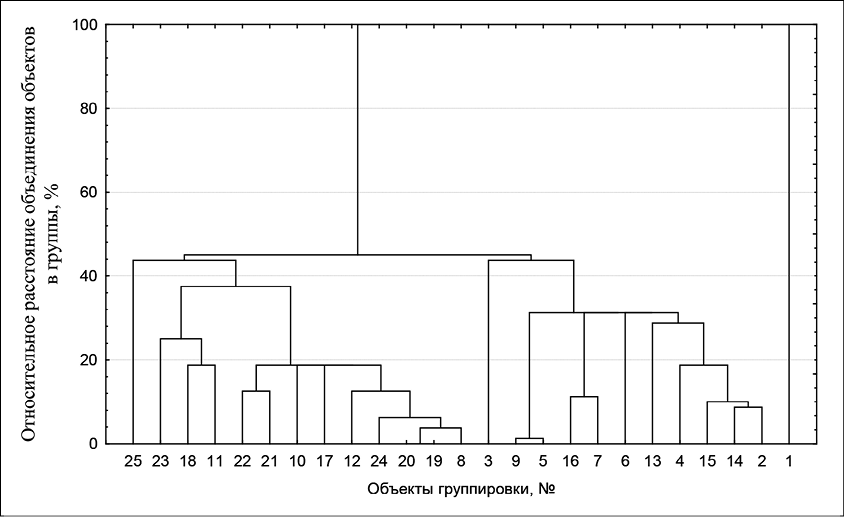
Дендрограмма объединения индивидуальных соединений (относительное евклидово расстояние) Примечание: составлена автором по результатам данного исследования
Используя, например, априорную информацию о наименее чувствительном компоненте (например, ТАТБ, столбец матрицы 1, табл. 1), можно построить ряд термической чувствительности (по увеличению чувствительности) некоторых штатных и перспективных соединений: ТАТБ < ТНТ < НМХ < НТО, HNIW < RDX < НЦ < ДНДЭГ, ДНТЭГ, PETN < ДИНА, ТМЕТН < НГЦ < НЭЭНТ, ADN < FTDO. Соединения опорных рядов выделены жирным шрифтом, а их порядок хорошо соответствует опорным рядам [1; 4; 6]. Матрица расстояний, как и разбиение совокупности данных на последовательность увеличивающегося количества L= 3; 4; 10 и 18 кластеров (табл. 1), позволяет определять наиболее близкие по обобщенной мере объекты. Это является основой выбора аналогов для оценки характеристик новых компонентов или в случае пропусков в данных, а также для определения признаков отличия [7, с. 112–125].
Например, нитротриазолы № 2 – НТО, № 14 – Э-3Н, № 15 – Э-3Н* близки по характеристикам термической чувствительности. В свою очередь, НЭЭНТ, содержащий нитротриазольную и нитроэфирную (как в структуре ДНДЭГ) группы, существенно менее термически стоек, чем ДНДЭГ и, например, Э-3Н. Несколько отличается от прогноза работы [1] и положение FTDO относительно НГЦ. Последний показывает неочевидную близость к ТМЕТN. Представляют несомненный практический интерес относительно – в сравнении с ADN, термически стойкие соли динитразовой кислоты № 9 и 10. Следует отметить устойчивость кластеров, включающих единичные объекты (например, ТАТБ, FTDO и, частично, ТНТ) при увеличении количества кластеров L, на которые разбивается совокупность данных. Полученные результаты кластеризации позволяют классифицировать и смесевые композиции на основе рассмотренных компонентов [8], определять доминирующие компоненты и смеси композиций по параметрам термического разложения и теплового взрыва [11, с. 113–126; 12, с. 124–1388]. Дополнительное тестирование показало, что полученная классификация ВВ достаточно устойчива при расширении количества признаков, например, за счет молекулярных дескрипторов [14] – пакет программ Dragon, или к введению бинарных признаков для некоторых функциональных групп [6; 7, с. 145–154].
Для группы данных, включающей инициирующие и вторичные ВВ из опорных рядов [4; 6], используются признаки, не связанные с классификацией ВВ по этим группам (табл. 2). Номера инициирующих ВВ [1; 2, с. 110–118; 3, с. 205–213] выделены в табл. 2 жирным шрифтом. В этой же таблице приведены значения евклидового расстояния (S) до объектов от ТНТ, выбранного в качестве эталона.
Таблица 1
Матрица евклидовых расстояний между объектами (усеченная)
|
№ объекта, шифр объекта |
№ объекта, евклидово расстояние (S) от диагонального элемента (эталона), стоящего на диагонали |
Количество кластеров, L, и принадлежность объектов к № кластера при заданном L |
||||||||
|
1 |
2 |
3 |
4 |
5 |
L= 3 |
L= 4 |
L= 6 |
L= 10 |
L= 18 |
|
|
1, ТАТБ |
0 |
92 |
63 |
74 |
142 |
1 |
1 |
1 |
1 |
1 |
|
2, НТО |
92 |
0 |
34 |
22 |
51 |
2 |
3 |
3 |
4 |
9 |
|
3, ТНТ |
63 |
34 |
0 |
30 |
81 |
2 |
3 |
3 |
3 |
3 |
|
4, HMX |
74 |
22 |
30 |
0 |
72 |
2 |
3 |
3 |
4 |
4 |
|
5, RDX |
142 |
51 |
81 |
72 |
0 |
2 |
2 |
6 |
7 |
5 |
|
6, HNIW |
118 |
27 |
61 |
45 |
29 |
2 |
2 |
6 |
7 |
6 |
|
7, ТНАД |
142 |
51 |
85 |
69 |
18 |
2 |
2 |
6 |
7 |
7 |
|
8, ДИАЗ-4 |
178 |
86 |
116 |
106 |
35 |
3 |
4 |
2 |
6 |
12 |
|
9, ГМС |
143 |
52 |
82 |
73 |
1 |
2 |
2 |
6 |
7 |
5 |
|
10, ГС |
192 |
101 |
129 |
122 |
50 |
3 |
4 |
2 |
10 |
10 |
|
11, ADN |
219 |
127 |
159 |
146 |
78 |
3 |
4 |
5 |
9 |
11 |
|
12, PETN |
180 |
88 |
120 |
107 |
40 |
3 |
4 |
2 |
6 |
12 |
|
13, ДНП |
112 |
23 |
50 |
45 |
31 |
2 |
2 |
6 |
5 |
13 |
|
14, Э-3Н |
86 |
7 |
32 |
15 |
58 |
2 |
3 |
3 |
4 |
9 |
|
15, Э-3Н* |
97 |
6 |
40 |
25 |
46 |
2 |
3 |
3 |
4 |
9 |
|
16, БЭФ |
135 |
45 |
79 |
61 |
24 |
2 |
2 |
6 |
7 |
7 |
|
17, ДИНА |
189 |
98 |
128 |
118 |
47 |
3 |
4 |
2 |
10 |
10 |
|
18, НЭЭНТ |
211 |
119 |
150 |
139 |
69 |
3 |
4 |
5 |
9 |
18 |
|
19, ДНДЭГ |
175 |
83 |
114 |
103 |
33 |
3 |
4 |
2 |
6 |
12 |
|
20, ДНТЭГ |
175 |
83 |
114 |
103 |
33 |
3 |
4 |
2 |
6 |
12 |
|
21, НГЦ |
196 |
105 |
138 |
122 |
59 |
3 |
4 |
2 |
6 |
15 |
|
22, ТМЕТN |
189 |
98 |
131 |
115 |
52 |
3 |
4 |
2 |
6 |
15 |
|
23, ДИАЗ-1 |
229 |
137 |
168 |
157 |
87 |
3 |
4 |
5 |
9 |
2 |
|
24, НЦ |
171 |
79 |
110 |
98 |
29 |
3 |
4 |
2 |
6 |
12 |
|
25, FTDO |
250 |
159 |
191 |
176 |
110 |
3 |
4 |
4 |
2 |
8 |
Примечание: составлена автором по результатам данного исследования
Таблица 2
Взрывчатые характеристики некоторых индивидуальных ВВ
|
№ ВВ |
ВВ |
Твсп, оС |
Q, ккал/кг |
Но, мм |
S от ТНТ |
|
1 |
ТНТ |
475 |
1050 |
240 |
0 |
|
2 |
Тетрил |
257 |
1150 |
130 |
264 |
|
3 |
Тетразен |
160 |
575 |
70 |
595 |
|
4 |
RDX |
260 |
1380 |
90 |
421 |
|
5 |
HMX |
335 |
1360 |
120 |
361 |
|
6 |
ТЭН (PETN) |
225 |
1460 |
100 |
500 |
|
7 |
НГЦ |
222 |
1545 |
30 |
594 |
|
8 |
ТНРС |
293 |
390 |
110 |
697 |
|
9 |
Гремучая ртуть |
170 |
425 |
70 |
716 |
|
10 |
АС |
330 |
408 |
110 |
671 |
Примечание: составлена автором на основе источников [1; 2, с. 110–154; 3, с. 172–189] и по результатам данного исследования (значения S).
Это позволяет построить общий опорный ряд инициирующих и вторичных ВВ по увеличению чувствительности и опасности: ТНТ, тетрил, НМХ, RDX, ТЭН (PETN), НГЦ, тетразен, ТНРС, АС, гремучая ртуть. Этот ряд хорошо соответствует опорным рядам чувствительности и опасности ВВ [2, с. 112–123; 3, с. 112–139; 4]. Некоторые вопросы вызывает положение тетрила в последовательности полученного ряда объектов, что не противоречит данным, приводимым в литературе для частных рядов чувствительности [1; 4; 6]. Дендрограмма объединения объектов (кластеризация) однозначно показывает два кластера, соответствующих инициирующим и вторичным ВВ.
Таким образом, приведенные результаты кластерного анализа позволяют сделать однозначное заключение о его эффективности при классификации ВВ: по типу, при построении рядов чувствительности и опасности, при определении аналогов, доминирующих компонентов и смесей и при решении других задач. Следует отметить, что пакеты Deductor, Minitab содержат опцию тестирования нового объекта на предмет отнесения к какому-либо кластеру или определения аналога, а также опцию группировки признаков.
Использование других подходов и методов, включая логико-структурный, корреляционный, факторный и дискриминантный анализы, нейросетевые алгоритмы, расширит, как показывают результаты представленного тестирования и данные ряда работ, информативность проведенной группировки и классификации, а также позволит получать корреляционные, функциональные и другие соотношения, в том числе инвариантные, с низким значением дисперсии результатов [13–15].
Выводы
Проведенные исследования позволяют сделать следующие выводы:
1. Выбран в качестве базового, статистический метод группировки и классификации энергетических материалов по характеристикам их термического разложения и теплового взрыва – кластерный анализ.
2. Определены матрицы расстояний (евклидовых) между объектами, проведена группировка и классификация широкой группы индивидуальных энергетических материалов, описаны процедуры выбора аналогов, построены дендрограммы и ряды чувствительности, в том числе опорные.
3. Показана эффективность использования методов кластерного анализа для многомерной классификации соединений различных классов и назначения, построения опорных рядов, установления близости или аналогичности объектов по совокупности признаков.



