Введение
На сегодняшний момент процесс обработки заявок в системах ИТ-поддержки внешних клиентов, получающих услуги телекоммуникаций, является затратным и длительным, поскольку на такие рутинные задачи, как классификация заявок и их эскалация, затрачивается большое количество ресурсов. Снижение подобных затрат возможно с помощью внедрения систем обработки заявок, что позволит сократить время их обработки, уменьшить трудозатраты и обеспечить прозрачность бизнес-процессов. В настоящее время разработано большое количество систем типа: Service Desk и Help Desk, которые хорошо справляются с различными задачами по оптимизации бизнес-процессов, но, несмотря на широкий спектр инструментов, которые предлагают данные решения, они не позволяют полностью оптимизировать такие задачи, как, например, классификация или приоритизация заявок (обращений). По этой причине становится нормой в эти системы внедрять технологии искусственного интеллекта, применение которых увеличивает эффективность работы систем в целом, сокращает время отклика и повышает удовлетворенность пользователей. Использование интеллектуальных решений позволяет повысить конкурентное преимущество компании за счет оптимизации ИТ-процессов, сокращения времени на обработку заявок, а также повышения удовлетворённости пользователей и клиентов, но необходимо при внедрении интеллектуальных решений применять технологии, соответствующие структуре системы, требованиям к ней с точки зрения реальных бизнес-процессов. Поэтому достаточно важной и актуальной задачей является исследование алгоритмов классификации, которые можно применять для оптимизации процессов обработки заявок.
Цель данной работы состоит в исследовании популярных алгоритмов классификации заявок в системах коммуникации. Для достижения цели требуется решить следующие задачи: 1) выявить преимущества и недостатки существующих подходов; 2) провести моделирование алгоритмов классификации; 3) оценить модели на основе различных показателей, и в итоге выбрать наиболее подходящий алгоритм классификации для оптимизации системы обработки заявок.
Материалы и методы исследования
Отметим особенности применения методов классификации заявок в системах коммуникации. Во-первых, во многих практических задачах невозможно использовать заранее известные методы или алгоритмы, поскольку механизмы генерации исходных данных неизвестны или имеющейся информации недостаточно для создания модели, описывающей источник данных. Говорят, что в таких ситуациях исследователь имеет дело с «черным ящиком», из которого поступают данные. В таком случае единственный вариант – анализировать доступную последовательность исходных данных и пытаться делать предсказания, улучшая модель по мере поступления новых данных [1; 2, с. 864; 3, с. 62]. Во-вторых, каждый экземпляр в любом наборе данных, применяемом алгоритмами машинного обучения, представлен с использованием одного и того же набора признаков, причем следует учитывать, что признаки могут быть непрерывными, категориальными или бинарными. В-третьих, если экземпляры имеют известные метки (набор размеченных данных для тренировки модели на всех этапах ее построения), то такое обучение называется обучением с учителем (Supervised Machine Learning, SML), в отличие от обучения без учителя (Unsupervised Machine Learning, UML), где экземпляры не имеют меток – используя эти неконтролируемые (кластерные) алгоритмы, исследователи надеются обнаружить неизвестные, но полезные классы объектов [4, с. 53]. В-четвертых, возможна ситуация, когда информация для обучения предоставляется системе из внешней среды (внешний тренер, учитель) в виде скалярного сигнала подкрепления, который является мерой того, насколько хорошо система работает. В этом случае обучающийся не получает указаний, какие действия следует предпринимать, а должен сам выяснить, какие действия приносят наилучшее вознаграждение, пробуя поочередно каждое из них – обучение с подкреплением (Reinforcement Machine Learning, RML) [5, с. 210]. Учитывая указанные особенности применения систем, отметим, что классификация заявок как задача машинного обучения относится к категории обучения с учителем, в которой модель обучается на разделении наблюдений на нескольо классов.
Процесс в обучении с учителем разделен на два этапа: обучение и тестирование [6; 7, с. 210]. Алгоритм, используемый для категоризации данных в один из несколько предопределенных классов, играет роль классификатора, основная цель которого состоит в том, чтобы научиться распознавать и правильно классифицировать новые данные на основе информации, полученной из обучающего набора данных.
Обзор математического аппарата алгоритмов обучения позволил выделить следующие алгоритмы в обучении с учителем, используемые для решения задачи классификации:
− искусственные нейронные сети (Artificial Neural Network, ANN) [8],
− наивный байесовский классификатор (Naive Bayes) [9, с. 34; 10],
− метод ближайших соседей (K-nearest Neighbor, k-NN) [4, с. 64; 11, с. 198],
− случайный лес (Random Forest) [4, с. 123; 12, с. 85],
− дерево решений (Decision Tree, DT) [4, с. 105; 12, с. 81],
− линейная регрессия (Linear Regression) [4, с. 380],
− поддерживающие векторные машины (Support Vector Machine, SVM) [13, с. 316],
− логистическая регрессия (Logistic Regression) [4, с. 241].
Искусственная нейронная сеть (ANN) представляет собой модель, которая эмулирует работу биологического нейрона, ее главная цель – воссоздать методы оценки данных, такие как классификация, обобщение и распознавание образов, используя простые распределенные и устойчивые обработчики данных, называемые элементами обработки (PE) или искусственными нейронами. Основное преимущество ANN заключается в том, что обучение модели приводит к изменениям в нейронах. Обработка данных осуществляется в распределенном параллельном режиме. ANN представляют собой мощные инструменты обработки данных, способные выявлять зависимости в наборе данных. В их основе лежат искусственные нейроны, каждый из которых имеет системный узел, включающий в себя связи с другими нейронами. В конечном итоге выходной нейрон получает взвешенную сумму входных данных и применяет нелинейную функцию к этой сумме, что дает окончательный результат для всей нейронной сети [8; 12, с. 379]. Наивный байесовский классификатор основывается на применении теоремы Байеса и предназначен для классовой классификации данных с независимыми признаками, то есть каждый из признаков независимо влияет на то, что объект принадлежит определенному классу. Метод K-ближайших соседей (k-NN) основывается на том, что объекты схожих классов стремятся находиться близко друг к другу в пространстве признаков. Для классификации нового объекта алгоритм находит k ближайших обучающих объектов и определяет его класс на основе мажоритарного голосования среди этих соседей. Параметр k является целым числом, заданным пользователем, и контролирует количество соседей, учитываемых в классификации [4, с. 64]. Для улучшения качества классификации можно использовать алгоритм «случайный лес» (Random Forest) [4, с. 123; 12, с. 85]. Он является расширением алгоритма дерева решений (основан на правиле: «Если <условие>, то <ожидаемый результат>»), использует ансамбль деревьев для предсказания классов объектов. Каждое дерево строится на случайном подмножестве обучающих данных и случайном подмножестве признаков. В результате каждое дерево в ансамбле отличается от соседнего, что позволяет уменьшить эффект переобучения и повысить качество предсказаний. Особенность линейной регрессии в том, что она предсказывает ценность неизвестных данных с помощью другого связанного и известного значения данных, математически моделирует неизвестную или зависимую переменную и известную или независимую переменную в виде линейного уравнения. Одним из наиболее популярных методов обучения, который применяется для решения задач классификации, является метод опорных векторов (SVM), основная его идея заключается в построении гиперплоскости, разделяющей объекты выборки оптимальным способом. Алгоритм работает в предположении, что чем больше расстояние (зазор) между разделяющей гиперплоскостью и объектами разделяемых классов, тем меньше будет средняя ошибка классификатора [13, с. 316]. Для поиска взаимосвязей между двумя факторами данных применяется метод логистической регрессии, эта взаимосвязь используется для прогнозирования значения одного из этих факторов на основе другого. Логистический регрессионный анализ обобщает метод линейной регрессии и вместо предсказания конкретного значения (как это делает модель линейной регрессии) выдает число на интервале от 0 до 1. Чтобы преобразовать любое число в указанный диапазон, используется логистическая функция – сигмоида, главным ее свойством является то, что она фактически независима от значений ее аргумента, поэтому результатом всегда будет число в интервале [0,1]. Таким образом, эту функцию можно рассматривать как удобный способ сжатия или упаковки значений, вычисляемых с помощью линейной модели [14].
Результаты исследования и их обсуждение
Результаты сравнения алгоритмов классификации приведены в таблице 1.
Для окончательного выбора подходящего алгоритма классификации было проведено имитационное моделирование алгоритмов. Оценивались алгоритмы на основе следующих показателей:
− пропускная способность – количество данных, обработанных алгоритмом за единицу времени,
− время отклика – время, которое требуется модели, чтобы обработать один запрос,
− точность – насколько правильно модель предсказывает данные.
Моделирование выполнено в системе RapidMiner, которая является средой для проведения экспериментов и решения задач интеллектуального анализа, визуализации и моделирования [15; 16].
Таблица 1
Сравнительный анализ алгоритмов классификации
|
Алгоритм |
Преимущества |
Недостатки |
|
ANN |
− эффективен при моделировании сложных нелинейных отношений между входными и целевыми переменными, − адаптивен к изменениям в данных, − масштабируемость (обработка больших объемов данных) |
− затратный при реализации вычислений, − необходим большой объем данных для обучения, − сложность интерпретации, − склонность к переобучению |
|
Naive Bayes |
− простота и скорость, − эффективность на небольших наборах данных, − хорошее обобщение, − хорошая обработка категориальных признаков |
− ограничение о предположении независимости признаков, − неспособность улавливать сложные взаимосвязи, − проблемы с несбалансированными данными, − чувствительность к качеству данных, − неэффективность при наличии коррелирующих признаков |
|
k-NN |
− простота, − отсутствие обучения, − адаптивность к изменениям, − хорошая производительность на небольших объемах данных |
− вычислительная сложность, − неэффективность на высокоразмерных данных, − чувствительность к выбору параметра k, − низкая эффективность на несбалансированных данных, − зависимость от метрики расстояния |
|
Random Forest |
− высокая точность, − устойчивость к переобучению, − эффективность на больших объемах данных, − масштабируемость – легко параллелизуется и может эффективно обрабатывать задачи на многопроцессорных и распределенных системах |
− сложность интерпретации, − сложность подбора гиперпараметров, − вычислительно затратный процесс |
|
DT |
− простота интерпретации, − не требует предобработки данных, − устойчивость к выбросам, − работает с нелинейными данными |
− склонность к переобучению, − неустойчивость к изменениям в данных, − неэффективность на больших объемах данных, − сложность обработки категориальных данных |
|
Linear Regression |
− простота интерпретации, − эффективность при линейной зависимости, − вычислительная эффективность |
− ограниченность в моделировании сложных взаимосвязей, − чувствительность к выбросам, − ограничение на количество признаков, − ограничения о предположении представления данных (линейность, нормальное распределение остатков, отсутствие мультиколлинеарности) |
|
SVM |
− эффективность в пространствах высокой размерности, − эффективное использование памяти, − адаптивность к различным типам данных, − устойчивость к переобучению |
− чувствительность к выбору параметров, − сложность интерпретации, − вычислительная сложность обучения на больших наборах данных |
|
Logistic Regression |
− простота интерпретации, − эффективность на больших объемах данных – тратит относительно небольшое количество ресурсов, − мало параметров |
− неэффективна в случае нелинейных зависимостей, − чувствительность к выбросам, − требуется предобработка данных для заполнения пропущенных значений |
Примечание: составлено авторами на основе полученных данных в ходе исследования.
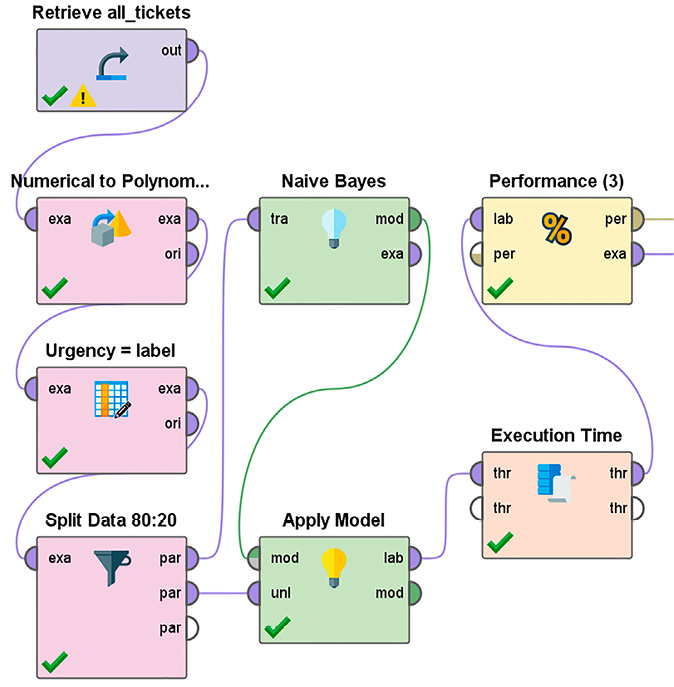
Моделирование алгоритма наивного байесовского классификатора
В качестве исходных данных были взяты данные о пользовательских заявках со следующими атрибутами: title, body, ticket_type, category, sub_category1, sub_category2, urgency, business_service, impact. Выполнено разделение данных на тренировочную и тестовую выборки в соотношении 80:20. Классификация выполнялась по срочности заявки. Оптимальные наборы гиперпараметров, то есть параметров, которые задаются в начале обучения, определены с помощью грид-оптимизации параметров (grid search). Grid Search заключается в переборе возможных параметров и выборе лучшей комбинации, которая дает наилучший результат. Пример организации имитационного эксперимента для наивного байесовского классификатора приведен на рисунке.
Отметим основные этапы моделирования алгоритма наивного байесовского классификатора: на предварительном этапе (общий для всех алгоритмов) подготавливаются данные для проведения эксперимента – на рисунке эти операции выполняют блоки Retriever all_tickets, Numerical to Polinom, Ugrency, Split Data, далее рассчитываются априорные вероятности принадлежности заявки к определенному классу, этот расчет во многом основывается на предварительных данных, как субъективных, так и объективных, и формируется функция правдоподобия как результат проведения статистического моделирования (блок Native Bayes). Для задачи классификации достаточно найти класс с максимальной апостериорной вероятностью. На заключительном этапе проводятся измерения выбранных ранее показателей модели (блоки Performance и Execution Time).
Результаты моделирования алгоритмов представлены в таблице 2.
Алгоритмы были ранжированы по каждому показателю, и для выбора лучшего применена интегральная оценка в виде суммы рангов – алгоритм с наименьшим рангом признается лучшим с точки зрения его влияния на эффективность процесса обработки заявок. При необходимости можно использовать и другой принцип сравнения, но очевидно, что в данном случае результат выбора не должен измениться – на основе выявленных преимуществ и показателей моделей наилучшим алгоритмом классификации для оптимизации системы обработки заявок является дерево решений.
Таблица 2
Сравнительный анализ алгоритмов классификации на основе метрик построенных моделей
|
Алгоритм |
Пропускная способность, заявка/c |
Ранг |
Время отклика, мс |
Ранг |
Точность, % |
Ранг |
Сумма рангов |
|
ANN |
43936,65 |
5 |
0,02276 |
5 |
87,19 |
3 |
13 |
|
Naive Bayes |
285588,24 |
2 |
0,00350 |
2 |
78,84 |
8 |
12 |
|
k-NN |
1017,07 |
8 |
0,98321 |
8 |
86,02 |
6 |
22 |
|
Random Forest |
11463,99 |
6 |
0,08722 |
6 |
86,76 |
4 |
16 |
|
DT |
571176,47 |
1 |
0,00175 |
1 |
88,69 |
1 |
3 |
|
Linear Regression |
147121,21 |
3 |
0,00679 |
3 |
86,69 |
5 |
11 |
|
SVM |
3124,19 |
7 |
0,32008 |
7 |
80,15 |
7 |
21 |
|
Logistic Regression |
87477,48 |
4 |
0,01143 |
4 |
87,59 |
2 |
10 |
Примечание: составлено авторами на основе полученных данных в ходе исследования.
Заключение
В результате исследования популярных алгоритмов классификации, выявления их особенностей применения, преимуществ и недостатков, а также проведения имитационного моделирования получены оценки показателей моделей и проведено их ранжирование. Это позволило выбрать наиболее подходящий алгоритм классификации для оптимизации системы обработки заявок – алгоритм дерево решений (decision tree). Для классификации заявок он может быть эффективным выбором для оптимизации процесса обработки за счет высокой точности и пропускной способности, легко интерпретируется для различных данных, требует небольшой и сравнительно простой предварительной обработки данных, а также способен обрабатывать как числовые, так и категориальные данные.



