Введение
Электролитно-плазменная обработка металлов и сплавов (ЭПО) – перспективный метод поверхностной обработки, сочетающий электрохимическое воздействие и локальный высокотемпературный разряд в электролите [1, 2]. При достаточно высоком напряжении на границе металл – электролит возникает парогазовая оболочка, ионная проводимость которой приводит к возникновению плазменного разряда между металлом (анодом) и электролитом (катодом либо специальным электродом) [3, 4]. Такая плазма в межэлектродном промежутке генерирует значительное тепло, вызывая нагрев поверхностного слоя металла, электролита и выделение пара [5, 6]. Контролируемый нагрев позволяет реализовать различные технологические процессы. Для понимания и управления такими процессами необходимо количественное соотношение между подводом энергии и ее распределением между различными элементами системы. В литературе описаны экспериментальные исследования температурных режимов электролитно-плазменных разрядов [3, 6]. В [7] описаны модели теплообмена в подобных системах. В частности, показано, что при определенных условиях температура активного анода не превышает ~100–110 °С, что позволяет выполнять полирование стали без отпускной выдержки и без структурных превращений в поверхностном слое [8].
Цель исследования – изучение распределения тепловых потоков в межэлектродном пространстве при различных условиях разряда в системах металлический электрод – плазма – электролит.
Материалы и методы исследования
Предположения при построении модели: геометрия межэлектродного промежутка рассматривается осесимметричной; парогазовая оболочка вокруг анода считается равномерной по толщине; стационарное состояние (установившийся тепловой режим) достигается за время импульса разряда.
Основу модели составляет баланс мощности, выделяемой в процессе разряда, и мощности, рассеиваемой в системе. Теплота выделяется за счет протекания электрического тока через плазму (джоулев нагрев) и за счет экзотермических реакций (например, окисление металла анода). Расходуется энергия на нагрев материалов и теплоотдачу в окружающую среду. Баланс тепла можно записать следующим уравнением:
Qe + Qreact = Qa + Qk + Qsol + Qvap + Qrad , (1)
где Qe – количество теплоты, выделяемое током в плазме и электролите; Qreact – теплота химических реакций (например, окисления анода); Qa и Qk – тепло, переданное соответственно аноду (детали) и катоду; Qsol – теплота, ушедшая на нагрев жидкого электролита; Qvap – тепловой поток, унесенный образующимся паром; Qrad – потери на излучение в окружающую среду. Левая часть уравнения (1) характеризует приход энергии, правая – ее распределение между компонентами системы [9, 10].
Каждый член баланса вычисляется на основе физических соотношений. Так, количество джоулевой теплоты определяется законом Джоуля – Ленца:
Qe = UIt, (2)
где U – напряжение между электродами; I – сила тока разряда; t – время (длительность воздействия в рассматриваемом режиме). Теплота реакции окисления металла анода рассчитывается как Qoxid = qV, где q – удельная теплота реакции (например, для окисления железа q ≈ 822 кДж/моль [11]), V – количество прореагировавшего металла (моль). Тепловые потоки Qa, Qk, Qsol a вычисляются путем решения уравнений теплопроводности и конвективного теплообмена для анода, катода и объема электролита соответственно, с граничными условиями, заданными конфигурацией задачи.
Для оценки теплоотдачи паром Qvap используется коэффициент теплообмена испарения, определенный по эмпирическим зависимостям [12, 13]. Потери на излучение Qrad оцениваются по закону Стефана – Больцмана, исходя из площади и средней температуры светящейся области разряда. Решение уравнения баланса (1) проводится итерационно до сходимости, при которой сумма тепловых потоков правой части равна общей выделенной теплоте (левая часть). Параметры модели (электропроводность плазмы, коэффициенты теплоотдачи и др.) подбираются согласно данным литературы [14, 15] и результатам собственных экспериментов.
Для верификации модели использованы данные по электролитно-плазменному полированию стали 20Х13 в струйном режиме [8]. Металлический образец (анод) площадью ~0.03 м² погружался в поток водного электролита (10 % водный раствор карбамида) при температуре ~25 °С. Катодом служил полый трубчатый модуль, через который подавался электролит (обратный поток). Напряжение источника питания варьировали от 0 до 500 В, ток в импульсном режиме не превышал 6 А. Температура на поверхности анода измерялась термопарой и плавкими индикаторами [16, 5]; также фиксировалась температура жидкости (в сборнике электролита) и пара (в уловителе). Погрешность измерений оценивалась в ±5 °С. Эти экспериментальные результаты использованы для сравнения с расчетными данными.
Результаты исследования и их обсуждение
Расчеты показывают, что до ~50–55 % энергии тока поглощается электролитом (водой) и уносится в виде нагревающейся жидкости. Около 10–15 % уносится испаряющейся влагой и излучением в окружающую среду. На нагрев самих электродов расходуется сравнительно меньшая доля энергии: порядка 30–35 % уходит в массивный катодный модуль и лишь 3–5 % – непосредственно в обрабатываемый металлический анод. Эти результаты соответствуют экспериментальным наблюдениям: температура небольшого анода повышается относительно умеренно, тогда как значительная часть выделившегося тепла рассеивается в объеме электролита и на стенках камеры [6, 10].
В таблице приведены расчетные стационарные температуры основных элементов системы для режимов, близких к максимальному тепловыделению в рассматриваемых экспериментах при 220 В и 5,5 А. Видно, что поверхность анода достигает порядка 110 °С, тогда как объемный электролит нагревается до ~90 °С. Температура парогазовой среды и стенок камеры также находится в пределах 100–110 °С. Эти величины хорошо согласуются с измеренными в экспериментах значениями [17], подтверждая адекватность модели. Отметим, что указанные температуры относятся к полировочному режиму, при котором отсутствует интенсивное искровое расплавление или оплавление материала анода [8].
В режиме же электротермического насыщения (например, плазменной цементации) целенаправленно достигаются более высокие температуры анода (600–900 °С) за счет использования иного состава электролита и увеличения энергии разряда.
Важным результатом моделирования является определение влияния режима разряда (приложенного напряжения, гидродинамических условий) на температурное состояние анода. Расчетная зависимость максимальной температуры поверхности анода от напряжения представлена на рисунке.
При погружении образца в неподвижный электролит (электролиз без плазмообразования) температура незначительно повышается с ростом U за счет омического нагрева электролита. Однако при достижении порога образования устойчивой парогазовой оболочки (~150–180 В для данных условий) наблюдается резкий рост температуры анода, связанный с переходом в режим развитого электролитно-плазменного разряда. Максимум температуры (~110 °С) соответствует интервалу 180–220 В, после чего при дальнейшем повышении напряжения температура несколько снижается. Модель объясняет это тем, что в области сверхкритических напряжений возникают неустойчивые разряды и интенсивное кипение (разбрызгивание электролита), что усиливает теплоотвод от анода и ограничивает дальнейший рост его температуры. Таким образом, существует оптимальный диапазон U, в котором локальный тепловой режим наиболее интенсивен.
Пример распределения температур между компонентами системы (расчет при U = 220 В, I = 5,5 А, время 30 с)
|
Компонент системы |
Температура, °C (стационарная) |
|
Поверхность анода (сталь 20Х13) |
110 ± 5 |
|
Жидкий электролит (в ванне) |
87 ± 5 |
|
Парогазовая среда (уловитель пара) |
105 ± 5 |
|
Стенки рабочей камеры |
100 ± 5 |
|
Катодный модуль (трубка) |
~30 |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
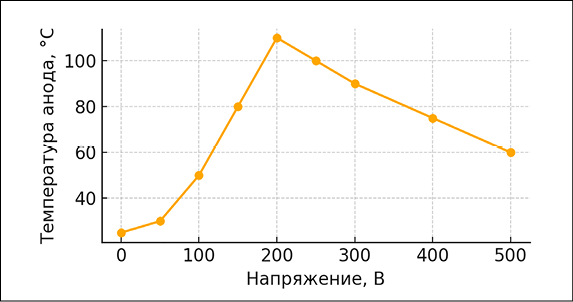
Зависимость максимальной температуры поверхности анода от напряжения между электродами (расчетные данные для стали 20Х13 в 10 %-ном растворе карбамида) Примечание: составлен авторами по результатам данного исследования
Данная картина соответствует экспериментально наблюдаемому характеру зависимости температуры анода от напряжения [18]. Добавление принудительной циркуляции электролита (струйный режим) приводит к снижению абсолютных значений температуры за счет улучшенного охлаждения поверхности. Например, при фокусированной струе электролита температура анода поддерживается на уровне лишь ~60–80 °С даже при 300–400 В, что используется для деликатного полирования без термического воздействия на структуру стали [8].
Результаты моделирования показывают, что энергетический баланс в электролитно-плазменной системе существенно смещен в сторону поглощения тепла электролитом. Это означает, что жидкая фаза электролита играет роль эффективного охлаждающего агента, отводящего более половины выделяемой энергии. Данный вывод согласуется с экспериментальными фактами: визуально наблюдается интенсивное кипение электролита вокруг нагретого электрода, а измеренная температура потока жидкости возрастает значительно (до ~80–90 °С) даже при умеренном разряде [17].
Нагрев металлического анода, напротив, относительно невелик – не более 100–120 °С в полировочных режимах. Это объясняется малой долей энергии, идущей непосредственно в твердый металл, и постоянным отводом тепла в объем электролита и на катод. Катодный модуль в проводимых экспериментах имел значительно большую поверхность и тепловую массу, чем анод, поэтому около трети тепла уходит в катод и рассеивается в окружающей среде (через систему охлаждения катодного узла). Таким образом, межэлектродное пространство функционирует как своеобразный кипящий калорифер, где электрическая энергия преобразуется преимущественно в тепло жидкой фазы.
Максимум на графике зависимости температуры анода от напряжения (рисунок) указывает на наличие наиболее эффективного режима с точки зрения локального нагрева поверхности. В случае электрополирования этот режим соответствует верхней границе стабильного горения разряда, дающего наивысшую температуру, не вызывая при этом дефектов поверхности. Экспериментально известно, что полирование сталей в электролитно-плазменном разряде протекает эффективно при напряжениях близких к порогу кипения электролита, после чего дальнейшее увеличение напряжения малоцелесообразно. С другой стороны, для задач термохимического насыщения (например, диффузионного насыщения углеродом или азотом) требуется максимальный нагрев поверхности. Этого достигают в режиме интенсивного искрового разряда (непрерывное кипение, режим разбрызгивания), при котором температура металлического анода может быть доведена до 600–800 °С и поддерживаться в течение необходимого времени обработки. Однако подобный режим сопряжен с риском эрозии и расплавления поверхности, поэтому важен компромисс между стабильностью разряда и интенсивностью нагрева.
Заключение
Построенная в данной работе математическая модель не учитывает сложных нестационарных эффектов – например, периодические колебания тока и образования пузырьков пара, которые могут приводить к колебаниям температуры. Тем не менее усредненные результаты баланса хорошо описывают общие тенденции, позволяющие оптимизировать режимы обработки. Так, на наличие наиболее эффективного режима с точки зрения локального нагрева поверхности указывает максимум в зависимости стационарной температуры анода от напряжения. В случае электрополирования этот режим соответствует верхней границе стабильного горения разряда, дающего наивысшую температуру, не вызывая при этом дефектов поверхности. Экспериментально известно, что полирование сталей в электролитно-плазменном разряде протекает эффективно при напряжениях близких к порогу кипения электролита, после чего дальнейшее увеличение напряжения малоцелесообразно. Дальнейшее развитие модели может включать учет динамики парообразования и гидродинамики потока электролита, а также влияние геометрии и размеров электродов. Кроме того, планируется расширить модель для различных составов электролита, что позволит прогнозировать температурные поля для процессов плазменно-электролитного азотирования, оксидирования и др., где возможны дополнительные источники или стоки тепла (эндо- или экзотермические химические реакции в плазме, растворение электродов и пр.).



