Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,279

Введение

Удовлетворение потребностей государства в квалифицированных (подготовленных к работе) кадрах – это одна из главных целей любого образовательного учреждения профессионального образования [1]. В частности, это декларируется в качестве первой цели в уставе Чувашского государственного университета (ЧувГУ) [2]. Качество подготовки таких кадров является важным фактором для определения конкурентоспособности образовательного учреждения [3].

Качество подготовки выпускника выражает совокупность степеней его подготовленности со стороны различных преподавателей. Отдельные преподаватели сообщают о степени подготовленности обучающихся при помощи итоговых оценок по своим учебным дисциплинам. Высокая оценка может служить мотивацией студенту для успешного освоения соответствующей дисциплины. Подробнее мотивирующие факторы для получения той или иной оценки студентом рассмотрены в работе [4]. Для информирования студентов об ожидаемых оценках возможно применение прогнозирования этих оценок. Кроме мотивации, с учетом получаемого прогноза возможно также проведение некоторых мероприятий с целью повышения успеваемости [5]. Об актуальности прогнозирования успешности обучения студентов сообщается, к примеру, М.В. Носковым и соавт. [6; 7].

Одним из подходов к прогнозированию оценок является использование искусственной нейронной сети (НС). Для применения НС требуется выполнить ее обучение. В ЧувГУ разработано приложение, позволяющее обучать НС, предназначенную для прогнозирования оценок по дисциплине «Базы данных». Ожидается, что, чем больше будет данных, тем точнее будут прогнозы [8, с. 20]. Например, в [9] сообщается об учете при прогнозировании 86 признаков. В связи с этим приложение позволяет при прогнозировании оценок учитывать приблизительно столько же – 84 фактора (признака).

Прогнозирование осуществляется при помощи НС, представляющей собой простой персептрон. Всего на входе НС m = 233 значения по каждому студенту, полученные из 84 признаков. Имеется входной слой, состоящий из 233 нейронов, и один выходной нейрон. Каждое из 233 входных значений подается на входы каждого из 233 нейронов входного слоя с помощью m2 дуг, обладающих весами. Как обычно в персептронах, каждый нейрон входного слоя вырабатывает выходное значение на основе функции активации (см. ниже) от суммы произведений входных значений на веса соответствующих дуг. Выходные значения каждого нейрона входного слоя подаются на вход выходного нейрона с помощью 233 дуг, имеющих веса. Выходной нейрон по такому же принципу, как и остальные нейроны, выставляет выходное значение, используя функцию активации.

Кодировка признаков осуществляется следующим образом. На входе НС часть факторов учитывается как прямое числовое значение, например средняя оценка за второй семестр, а другая часть – как значение 0 или 1, выражающее принадлежность к тому или иному кластеру, например, к одной из 12 групп административно-территориальных районов. Существуют такие признаки, которые учитывают широкий диапазон чисел, например число жителей населенного пункта, откуда прибыл студент. В данном случае в качестве входного значения используется десятичный логарифм указанного числа, таким образом, диапазон значительно сужается, наподобие нормирования признаков. Некоторые признаки нормируются, например балл ЕГЭ по физике делится на 100 как на максимальное значение. В итоге все признаки представлены небольшими числами от 0 до 7, среди них нет стремящихся к нулю.

Задача обучения НС может быть выражена как задача оптимизации:

f(x)→min,

где x – набор входных данных:

1) матрица n×m, в которой каждая строка соответствует одному из n студентов, а столбец – одному из m значений параметров, присущих студентам; min ≥ 0; min ∈ R, где R – множество действительных чисел; f – целевая функция;

2) вектор-столбец итоговых оценок, по одной оценке Oi на студента, i = 1,…,n, где n – число студентов,

при ограничениях на неравенства и принадлежность к доменам, присущим каждому из указанных 233 значений. Например, значение «средний балл за 2 семестр» является вещественным числом от 2 до 5. Имеются некоторые специфические ограничения: например, студент может быть из одной и только одной группы административно-территориальных районов.

Поскольку числовое значение на выходе крайнего правого нейрона, обозначаемое S, однозначно определяется из совокупности весов дуг, обозначаемой W, и m входных значений НС, целевая функция может быть выражена как усредненное по всем студентам значение табличной функции от значения Si на выходе крайнего правого нейрона и оценки Oi, полученной студентом по дисциплине «Базы данных»:

,

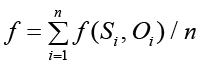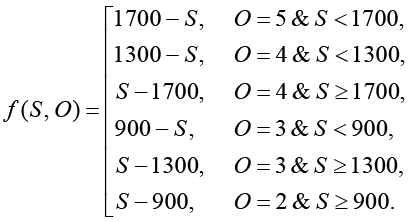
где Si определяется как значение функции возбуждения нейрона (см. ниже).

При обучении НС некоторыми разработчиками применяется метод обратного распространения ошибки [10, с. 174]. Разработан программный модуль, реализующий данный метод для рассматриваемой сети, однако при анализе его кода выявлена положительная обратная связь, приводящая к чрезвычайному увеличению весов дуг (до значений 10 в 308 степени и т.п.). Это не только противоестественно, но и, в свою очередь, приводит к аварийному завершению программы из-за ошибок операций с плавающей запятой еще при неприемлемо высоких значениях целевой функции (около 180, см. контрольные значения ниже).

Другой вариант оптимизации весов дуг – использование метода однокоординатного спуска (ОКС), однако он работает неприемлемо долго. Реализация метода ОКС показывает, что для совершения всего одной итерации (то есть исследования изменений в каждой из координат) требуется около 4 ч машинного времени на указанной ниже вычислительной системе.

Время одной итерации для метода ОКС пропорционально произведению числа студентов n на число координат (m2 + m, поскольку одна координата – это вес одной дуги НС), на время однократного вычисления целевой функции (пропорционально m2 + m) и на количество экспериментальных значений для одной координаты (около 20). То есть временная сложность составляет nm4. Можно попытаться несколько оптимизировать время вычислений за счет хранения части промежуточных результатов в дополнительных массивах, однако при этом потребовались бы массивы вещественных чисел размерностью m ×m × n, что затратно по размеру требуемой оперативной памяти. В связи с этим актуальна разработка более эффективного алгоритма обучения рассматриваемой НС.

Цель данного исследования – разработка практически реализуемого алгоритма обучения НС для прогнозирования оценок обучающихся. Решаемые задачи: разработать базовый алгоритм, произвести его программную реализацию, исследовать параметры алгоритма на оптимальность с помощью вычислительных экспериментов.

Материал и методы исследования

В качестве тестового примера рассматривается прогнозирование оценок 126 обучающихся в бакалавриате 3-го курса на кафедре компьютерных технологий ЧувГУ по дисциплине «Базы данных» за 2 года, по очной и очно-заочной формам обучения. В наборе данных имеются следующие оценки: «отлично», «хорошо», «удовлетворительно», «неудовлетворительно». Данные получены из информационных систем ЧувГУ «Личный кабинет и портфолио обучающихся ЧувГУ», служебного портала ЧувГУ, годовых отчетов студенческого научного общества факультета, бумажного рабочего журнала преподавателя и других бумажных документов. Учитывается 84 признака студента. Студенты, по которым не удалось собрать все данные, не учитываются в исследовании. Полученный набор данных случайным образом делится на обучающую и контрольную выборки в соотношении, близком к используемому в [11] соотношению, то есть 101 : 26 ≈ 80 : 22, при этом для балансировки классов целевой переменной по каждому из классов, то есть для каждого из четырех значений оценки, отбирается приблизительно 80 % соответствующих студентов. Так обеспечивается наличие представителей всех классов в контрольной выборке.

Общим методом исследования является проведение вычислительного эксперимента с вычислительной системой: ноутбук с процессором Intel(R) Core(TM) i5-7200U, 2712 МГц. Результаты эксперимента обрабатываются методами математической статистики. Выявление оптимальных параметров алгоритма оптимизации весов дуг НС представляет собой метаоптимизацию. При обучении НС используется кросс-валидация типа K-fold [12]. Сокращение набора признаков производится с помощью алгоритма AdDel, принцип работы которого сообщается в [11, с. 470]. Исследования производились с 05.12.2024 по 18.11.2025.

Разработка базового алгоритма

Предлагаемый алгоритм может рассматриваться как одна из вариаций стохастического градиентного спуска, нередко применяемого в машинном обучении [13]. Особенности данного алгоритма:

− целевой функцией f при оптимизации весов дуг является функция, напрямую зависящая от среднего отклонения по модулю вычисленных НС оценок от фактических для всех студентов из обучающей выборки;

− исследуется окрестность текущей точки многомерного пространства, координаты которой представляют собой веса дуг НС;

− производится ряд случайных изменений в относительно небольшом числе случайно выбранных координат (практически используется 120 изменений, то есть изменения производятся в 0,22 % координат);

− при нахождении удачных изменений формируется вектор изменений Δ, вдоль которого производятся новые изменения в координатах. При разработке алгоритма первая версия не предусматривала формирования такого вектора, производился каждый раз новый независимый ряд изменений, при этом оптимизационный процесс, как правило, останавливался в локальных экстремумах с неприемлемо высокими (около 60) значениями f;

− при удачном, то есть приводящем к снижению f, перемещении текущей точки вдоль Δ, все компоненты вектора Δ умножаются на число 2 и происходит повторное перемещение по полученному вектору, и так несколько раз. Число подобных перемещений определяется виртуальным числом, которое не должно превышать максимума, например 100, показывающего, сколько могло было быть сделано перемещений без умножения Δ на 2. Ранние варианты алгоритма не предусматривали умножения на 2, при этом скорость работы была существенно ниже. Максимум используется для приближения к принципам естественной НС, в которой веса дуг не могут стремиться к бесконечности.

Базовый алгоритм обучения НС следующий.

1. Загрузить:

1.1. Обучающую выборку, путем загрузки всего набора данных и загрузки сведений о разделении этого набора на обучающую и контрольную выборки.

1.2. Совокупность весов дуг НС, обозначаемую W.

1.3. Сведения об активности признаков.

2. Установить параметры:

2.1. Промежуточное число итераций H.

2.2. Максимальное число изменений НС на итерации Nmax.

2.3. Число изменений K в Δ.

2.4. Общее число совершенных итераций It ← 0.

3. Повторять H раз, то есть совершать итерации:

3.1. Сделать копию W, обозначаемую W1.

3.2. Вычислить целевую функцию f0 = f (W).

3.3. Установить число N изменений НС на данном шаге как случайное число от 1 до Nmax.

3.4. Произвести N случайных изменений в W1, равномерно распределенных между входными и выходными связями (дугами входного и выходного слоев) по их количеству. Изменения представляют собой действительные числа от -5 до +5 с точностью до 3 знаков после запятой. Очистить Δ и сохранить сведения об изменениях в Δ.

3.5. Вычислить целевую функцию f = f (W1).

3.6. Если f ≥ f0, то перейти к следующей итерации цикла по H.

3.7. Иначе:

3.7.1. Скопировать f0 ← f, W ← W1. Установить фактор масштабирования Fm ← 0,5.

3.7.2. Отобразить на экран номер итерации, N, f.

3.7.3. Установить счетчик шагов c ← 0.

3.7.4. Повторять, пока c < 100:

3.7.4.1. Удвоить Fm; c ← c + Fm. То есть произвести виртуальное увеличение c на удвоенное значение.

3.7.4.2. Выполнить повторные изменения в весах дуг W1 на соответствующие значения Δ, умноженные на Fm.

3.7.4.3. Вычислить целевую функцию f2 = f(W1).

3.7.4.4. Если f2 < f0, то:

3.7.4.4.1. Скопировать f0 ← f2, W ← W1.

3.7.4.4.2. Отобразить на экран номер итерации, N, f2.

3.7.4.4.3. Перейти к следующему шагу (п. 3.7.4).

3.7.4.5. Иначе:

3.7.4.5.1. Произвести обратные изменения в W1 по информации из Δ, то есть изменения по направлению, противоположному Δ.

3.7.4.5.2. c ← c + 7, то есть произвести виртуальное увеличение c на 7.

3.7.4.5.3. Перейти к следующему шагу (п. 3.7.4).

4. Отобразить на экран It и улучшение в целевой функции, полученное за шаг 3.

5. Если f > 0 & It < 200000, при указании пользователя откорректировать H, Nmax, K и перейти к шагу 3.

6. Сохранить W как результат обучения. Конец.

Алгоритм является стохастическим, вследствие чего его временная сложность как функция точно не определяется, однако можно утверждать, что он многократно для каждого из n студентов использует подпрограмму вычисления целевой функции с временной сложностью m2.

Результаты исследования и их обсуждение

Произведено исследование работы предложенного алгоритма с помощью программной реализации с целью разработки наиболее оптимального алгоритма из некоторых вариантов. Модификации алгоритма, образующие различные варианты, такие:

1. В п. 3.7.4.5, если Fm > 1, производить также уменьшение Fm в четыре раза, предполагая, что можно успешно перемещать текущую точку в направлении Δ, но не в два раза дальше, чем ранее, а только в 0,5 раза.

2. Между п.п. 3.7.4.5.1 и 3.7.4.5.2 вставить еще один пункт – выполнить K случайных преобразований Δ, если Fm < 1 (либо Fm ≤ 1), так как существует вероятность, что если текущая точка ранее успешно перемещалась в этом направлении, она будет успешно перемещаться в немного измененном направлении.

Использовались как различные наборы признаков, генерируемые случайным образом, так и один и тот же набор признаков. В каждом эксперименте оптимизация производилась от исходного значения f (около 1207) до контрольных значений – 100, затем 10. Значения 1 и тем более 0 в некоторых случаях оптимизационный процесс не достигал, несмотря на работу свыше 2 часов, что выяснилось в результате седьмого по счету запуска этого процесса, поэтому до таких значений оптимизация далее до некоторого момента не рассматривалась.

Всего выполнено 48 подобных экспериментов. Средние значения времени достижения значений f = 100 и f = 10 для различных вариантов алгоритма следующие (в секундах):

1. С уменьшением Fm и случайными преобразованиями Δ – 26,5 и 236.

2. Без уменьшения Fm, но со случайными преобразованиями Δ – 19 и 130,5.

3. С уменьшением Fm, но без случайных преобразований Δ – 69 и 722.

4. Без уменьшения Fm и без случайных преобразований Δ – 27 и 206.

Таким образом, наивысшую скорость работы показывает вариант 2, который представлен вышеизложенным алгоритмом.

Исследована функция возбуждения (называемая также передаточной функцией, функцией активации) нейрона F для варианта 2 как наиболее перспективного. Использовались следующие значения: максимальное значение порога возбуждения p2 = 500, а минимальное: p1 = 0,95p2. В качестве функции возбуждения вначале применялась кусочно-линейная функция, состоящая из трех линий, которая описывается следующим образом.

До достижения суммарного значения на входе σ = p1 значение F = (σ – p1) / 1000. При p1 ≤ σ ≤ p2 функция линейно возрастает по формуле F = (σ – p1) / (p2 – p1) до значения F = 1, и далее вычисляется по формуле F = 1 + (σ – p2) / 1000. Это значение выставляется на выход нейрона.

Однако обычно чаще в литературе говорится об использовании гладкой функции возбуждения. Проанализировано использование в базовом алгоритме такой функции на основе плавной функции знака – softsign [14] со смещением: F = (σ – p) / (|σ – p| + 1), где p – смещение относительно начала координат (центр порога), p = 0,975p2. Выполнено 20 экспериментов, в результате выявлено, что при p = 0 алгоритм сходится к значению 10 примерно в 1,67 раз быстрее, чем при p = 487,5. Для применения метода обратного распространения применялся также другой вид гладкой функции возбуждения – логистическая функция (сигмоида) [10, с. 170], однако в этом случае требуется проверка ограничений для возведения в степень во избежание ошибок арифметического переполнения. Наложение подобных ограничений приводило к остановке оптимизационного процесса в локальных экстремумах, поэтому далее сигмоида не рассматривалась.

Применение гладкой или кусочно-линейной функции практически не оказывает влияния на скорость сходимости при p = 487,5, то есть при смещении порога относительно 0, равном 487,5.

Исследовано влияние величины порога на скорость сходимости к f ≤ 10 при кусочно-линейной функции возбуждения. Для этого проведено по 10 экспериментов для каждого из трех значений p2 ∈ {1,10,500}. При p2 = 500 среднее время сходимости составило 118,6 с, при p2 = 10 составило 95,9 с, при p2 = 1 соответственно 92,2 с. Значение p2 = 0 не исследовалось, поскольку минимум порога в таком случае будет совпадать с его максимумом.

Таким образом, целесообразно использовать несмещенный относительно 1 порог. Далее в экспериментах использована гладкая функция возбуждения на основе функции softsign и параметры, оптимальность которых выявлена путем проведения ряда экспериментов с варьированием этих параметров:

1. Число случайных преобразований (при добавлении таких преобразований после п. 3.7.4.5.1 базового алгоритма) K = 10.

2. Константа cstop = 100 во фразе «повторять, пока c < 100» (см. п. 3.7.4 базового алгоритма; число 100 программное приложение позволяет изменять на другое целое число).

3. Центр порога возбуждения p = 0,975, что соответствует значению p2 = 1.

4. Nmax = 120.

Для повышения эффективности базового алгоритма выполнено:

1. Сокращение набора признаков с помощью алгоритма AdDel. В итоге используется 33 признака из 84. Это направлено не только на сокращение времени по сбору исходных данных, но и на избежание проблемы «переобучения» НС [15].

2. Кросс-валидация типа K-fold. При этом исследована зависимость точности прогнозирования от количества подмножеств (так называемых «фолдов»), на которые делится обучающая выборка набора данных: для 14 значений количества от 4 до 50 проведено в среднем по 25,7 экспериментов. Выявлена наибольшая целесообразность деления набора данных x на nfold = 11 подмножеств x1,…,x11, что уточнено проведением повышенного количества (40) экспериментов с этим значением. Точность выше на 4 % от среднего значения точности для 14 вышеуказанных значений. При этом усредненное время обучения для разных значений количества изменяется от -4 до +61 % по сравнению с временем при nfold = 11.

При использовании кросс-валидации исследована зависимость качества прогнозов от метода приближения к минимуму f в обучающей выборке. Для выявления среднестатистических показателей произведено по 10 раз обучение тремя методами (30 экспериментов):

1. Обучение по каждому xi (i = 1,…,11) непосредственно до f(xi) = 0, то есть f(xi) → 0.

2. Сначала обучение по каждому xi (i = 1,…,11) до значения f(xi) = 100, затем то же, но до f(xi) = 10, затем, аналогично, до f(xi) = 0, что обозначим как f(xi) → {100,10,0}.

3. По аналогии с предыдущим методом, но вместо трех значений с пятью значениями f(xi): 100, 20, 7, 1, 0, что обозначим как f(xi) → {100,20,7,1,0}.

Обученные таким образом НС затем применялись для прогнозирования оценок в контрольной выборке. Наименьшее число ошибочных прогнозов получено третьим методом; первый метод производит в среднем на 16 % больше таких ошибок, а второй на 5 % больше. Время работы для этих трех методов отличается ненамного: второй метод наискорейший, третий требует в среднем на 10 % больше времени, а первый – на 24 %.

Поскольку число ошибок важнее при незначительном отличии скорости работы, наилучшим следует считать третий метод.

Усредненные значения достигаемой точности и времени исполнения при вариации параметров алгоритма

Примечание: составлена авторами на основе полученных данных в ходе исследования.

Числовые показатели обучения по данным экспериментов с оптимальными параметрами алгоритма следующие:

− среднее время работы составляет 81 с (от 50 до 152 с) при среднеквадратическом отклонении 31 с;

− среднее количество ошибочных прогнозов в контрольной выборке 27,1 %, то есть точность прогноза 72,9 % (6,8 ошибок из 25, от 4 до 10 ошибок). Это можно считать приемлемым результатом: например, в [1] сообщается о точности прогноза 67 % и выше.

Затем проведена серия дополнительных экспериментов. При следующей совокупности значений параметров алгоритма (назовем ее базовой) наблюдается повышенная точность прогнозирования при относительно небольшом времени исполнения:

– количество признаков сокращается в соответствии с алгоритмом AdDel;

– f(xi) → {100,20,7,1,0}; cstop = 100;

Nmax = 120; K = 10; nfold = 11;

– уменьшение Fm не осуществляется;

– функция активации softsign со смещением p = 0,975.

В таблице приводятся усредненные сведения о достигаемой точности и затрачиваемом для этого времени при изменении одного из параметров по сравнению с базовой совокупностью с указанием количества проведенных при этом экспериментов.

В приведенных данных только при cstop = 1000 точность выше, чем при базовой совокупности значений параметров, однако при этом время выполнения увеличивается более чем вдвое. Остальные изменения характеризуются более низкой достигаемой точностью. Таким образом, базовая совокупность – это, с высокой вероятностью, оптимум, во всяком случае, локальный, для задачи выбора оптимальных значений параметров.

Заключение

Применение кросс-валидации позволяет значительно чаще достигать нулевых ошибок при обучении НС. Без использования данного метода оптимизационный процесс практически останавливался в локальном минимуме в одном из нескольких экспериментов. С использованием кросс-валидации такого не произошло ни в одном из 600 выполненных подряд экспериментов.

Выявлены следующие значения параметров и варианты использования алгоритма, применение которых представляется целесообразным с точки зрения скорости сходимости и количества ошибочных прогнозов:

− в векторе изменений после безрезультатного перехода по нему выполняются случайные преобразования в количестве K = 10;

− максимум виртуального числа повторных переходов по вектору изменений – 100;

− функция возбуждения гладкая на основе softsign с центром порога срабатывания нейрона p = 0,975;

− максимальное число изменений весов дуг для формирования вектора изменений Nmax = 120.

− уменьшения фактора масштабирования не производится;

− кросс-валидация типа K-fold с делением набора данных на 11 подмножеств и последовательным обучением по каждому подмножеству до пяти убывающих значений целевой функции, заканчивая нулевым.

Программное приложение, реализующее предложенный алгоритм, позволяет прогнозировать не только итоговую оценку по дисциплине «Базы данных», но и средний балл по всем дисциплинам за 5 семестр. Таким образом, алгоритм обладает определенной универсальностью.

Вышеизложенный алгоритм с модификацией, представляющей собой перебор сочетаний по три признака, реализуется магистрантами кафедры компьютерных технологий в качестве лабораторной работы по выбору наиболее информативной системы признаков для прогнозирования на наборах данных по вариантам.