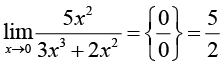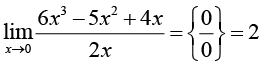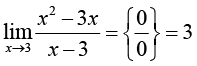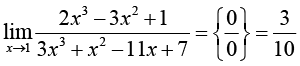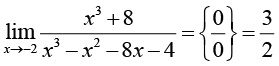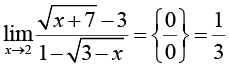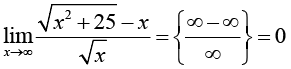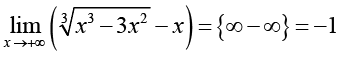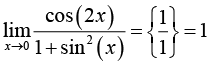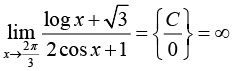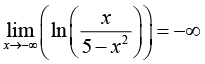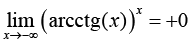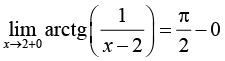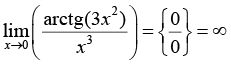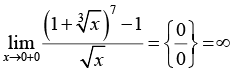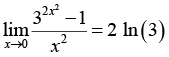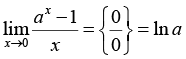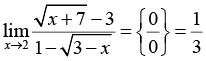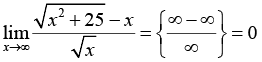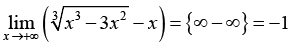Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,279

Введение

Современное общество переживает стремительное развитие цифровых технологий, и особенно заметную роль в этой трансформации играет искусственный интеллект (ИИ), реализуемый в виде генеративных сетевых решений. Сегодня ИИ активно внедряется в различные сферы жизни человека: медицину, промышленность, транспорт, бизнес, науку и образование. Для большинства людей ИИ становится доступным и применимым в повседневной жизни, как волшебный «черный ящик», который подсказывает решения. Технологию уже не отменить, даже если есть такое желание, и актуальны вопросы об адаптации к ней, оптимальном использовании и о том, как сложится будущее [1, 2].

Особенно ощутимо влияние ИИ в сфере образования. Школьники и студенты все чаще прибегают к использованию «интеллектуальных помощников» для решения домашних заданий, поиска информации, подготовки к экзаменам и объяснения сложных тем, мотивируя выбор такого пути потенциальным упрощением в понимании теоретических материалов, помощью в решении сложных математических задач, получении пошаговых объяснений. Может быть поставлен вопрос не только о влиянии ИИ-технологий на учебные результаты, но и на общее восприятие студентами выбранной сферы профессиональной деятельности, на социальные и профессиональные установки: будущий инженер совершенствует компетенции курьера, а не конструктора-изобретателя, отклоняясь он привычного образа [3, 4]. Нет сомнений, что невиданная ранее доступность информации сомнительного качества и ее комбинаций, предоставляемая новым продуктом, изменит сферу профессионального образования, но понимание того, как и когда сбалансируются интересы разных заинтересованных сторон, действующих в этой сфере, пока отсутствует, хотя уже стало предметом зарубежных теоретических исследований, например [5–7] и др. Появились актуальные отечественные результаты, представленные в [8–10] и др. Проводятся опросы пользователей нейросетевых моделей, с результатами которых можно познакомиться в [11–13] и др.

Оптимистический взгляд на применение нейросетевых технологий в обучении состоит в том, что этот инструмент может стать мощным средством для повышения эффективности учебного процесса. Искусственный интеллект способен не только давать готовые ответы, но и обучать: подсказывать, направлять, задавать вопросы и вовлекать в процесс. Таким образом, ИИ можно рассматривать как персонального помощника студента, который всегда доступен, терпелив, этически комфортен и поможет справляться с учебной нагрузкой.

Пессимистический взгляд на новую ситуацию вскрывает риски некритического использования предлагаемых решений, подмену и избегание обучающимся собственных интеллектуальных усилий и, как следствие, снижение качеств тех изменений, которые ожидаются от студентов в педагогическом процессе, ориентированном не на получение правильных ответов «для отчетности», а на действительное научение, изменение студента. Здесь, с учетом профессиональной инерции преподавателей, появляется источник отрицательных эмоций: учебные задачи в привычных объемах успешно решены студентами и с привычными трудовыми затратами проверены преподавателем, вопросов у студентов нет, а в контрольных мероприятиях и собеседованиях обнаруживается аморфность знаний, приемы принятия решений студентами не усвоены. Как следствие, результаты педагогического взаимодействия кажутся неудовлетворительными, поставлены невысокие оценки, все недовольны… Основные ожидания, связанные с ИИ-технологиями, имеют в России направленность на автоматизацию планирования или проверки студенческих работ и подобные вопросы [14] (обостряя до абсурда, мы имеем шансы увидеть битву ИИ-проверки с ИИ-решателями без живых преподавателей и студентов). Эффективные способы временно, для проведения объективного контроля усвоенных студентами знаний, запретить неконтролируемое использование студентами новых возможностей или надежно отличить результаты, полученные без них, от результатов, полученных «нечестно», практически отсутствуют [12, 14]. Наблюдается явный дефицит идей продуктивного использования новых материалов такой природы в качестве инструмента обучения.

В работе Я. Кузьминова можно найти предложение о прямом педагогическом внимании к тому, как обучающийся может находить ошибки в ИИ-решениях [15]. В развитие этой линии, предлагается возможность использования новой формы проблемных учебных заданий: поиск типовых недочетов в предложенных ИИ-решениях с педагогической поддержкой в виде их классификации, когда студенту надо не просто обнаружить недочет, но отнести его к тому или иному типу, как сделано в данной работе, либо, наоборот, систематически проверять ИИ-решение на наличие в нем недочетов перечисленных типов.

Для предметной основы исследования выбрана тематика, связанная с нахождением пределов элементарных функций, замечательная по возможности применения разных стилей решения, необходимости частого обращения к теоретическому аппарату (теоремам о свойствах бесконечно больших и малых величин, основным теоремам о пределах, «замечательным» пределам и таблице эквивалентных бесконечно малых величин), высоким требованиям к алгебраической эрудиции обучающихся и знанию свойств основных элементарных функций. Во многих задачах процесс решения не прозрачен заранее, так как неожиданно могут появляться (или не появляться) неопределенности и выходы на границы области определения используемых функций, оказывается необходимым не просто применение стандартной техники, а мини-исследование. Своеобразной ловушкой для ИИ-решателя является возможность использования для нахождения пределов эффективных приемов, выходящих за предполагаемые рамки изученного студентами материала: дифференциального исчисления и разложения функций в степенные ряды. Предполагается, что выявленные особенности использования нейросетевых инструментов в той или иной степени характерны для большинства других разделов учебного курса математики в техническом вузе, а в некоторой степени – вообще для процессов принятия решений в инженерной деятельности.

Цель исследования. В рамках данной работы в качестве основного объекта рассматриваются решения несложных типовых задач из раздела «Введение в математический анализ» по нахождению пределов элементарных функций (традиционно входящего в программы курсов «Математика» технических вузов), предлагаемых специализированными нейросетевыми решателями (использованы ChatGPT-4o, Gemini, Grok, DeepSeek). Исследование в своей основе направлено на выявление общих особенностей этих решений и оценку потенциала их использования в учебном педагогическом взаимодействии в рамках указанного раздела курса «Математика», а также, в качестве обобщения, на улучшение понимания перспектив его влияния на образовательный (учебный и воспитательный) процесс и ожидаемые результаты педагогического взаимодействия всего курса, исходя из методологического предположения об эволюции системы в сторону нового баланса интересов взаимодействующих сторон. Следующий уровень обобщения – осторожная перспективная оценка возможных эффектов в профессиональном становлении будущих инженеров.

Материал и методы исследования

С использованием типовых заданий, доступных в учебной литературе и в раздаточных материалах учебных курсов, в интерфейсах нескольких доступных специализированных нейросетевых решателей были сформулированы запросы и получены характерные ответы. Эти тексты, разделенные по типам задач, подверглись анализу с целью выявления процедурных недостатков в предложенных решениях, промежуточных и итоговых результатах. Некоторые примеры были добавлены для уточнения возникающей картины. Затем замечания к решениям были типизированы и решения соотнесены с замечаниями (по их типам), что позволило перейти к элементарной числовой (статистической) обработке таких данных и сформулировать общие выводы.

Результаты исследования и их обсуждение

В ходе исследования были выделены типы недочетов, характерных для сгенерированных нейросетями текстов решений:

A – критические фактические ошибки, приводящие к неправильному результату, и очевидные логические нарушения: «циклическая» логика и т.п.;

B – вульгарное некорректное обращение с терминологией («х = ∞», «предел расходится» и т.п.), некорректные алгебраические выражения со знаком «∞» в аргументах функций и алгебраических операций;

C – неосторожное применение конечной подстановки, влекущее (или потенциально влекущее) неопределенность или выход из области определения исследуемой функции, без предварительной проверки соответствующих условий или оговорки о пробном характере такого действия;

D – использование приемов дифференциального исчисления: правила Лопиталя, разложения в функциональный степенной ряд (без указания доступной альтернативы), условно недоступные студентам во время изучения раздела «Введение в математический анализ»;

E – применение малоизвестных алгебраических приемов («синтетическое деление», «Бином Ньютона для старших членов» и т.п.) и неназванные алгебраические приемы, имеющие доступные альтернативы в процедурах, предположительно известных студентам по школьному опыту;

F – другие ошибки, имеющие значение для понимания хода решения, в том числе стилистические ошибки, неясные фразы, англицизмы («факторизация», то есть разделение на множители и т.п.).

Соотношение между задачами (запросами) и обнаруженными недочетами показано в табл. 1–4. Общий текстовый объем всех полученных ИИ-решений существенно превосходит возможности статьи, поэтому после каждой таблицы приведен краткий комментарий по ней и избранные образцы решений с наглядными недочетами.

Самый частый недочет, характерный для ИИ-решений простых задач с алгебраическими элементарными функциями (табл. 1), – неосторожное применение конечной подстановки, способное завести решение в логический тупик (типа С); такие ошибки легко предотвратить ценой небольших дополнительных затрат: либо предварительно оговорить пробный характер действия (при неудаче – понятный возврат в главную логическую цепочку), либо предварительной проработкой элементов «от простого к сложному».

Таблица 1

Пределы с потенциальными неопределенностями, допускающими разрешение через элементарные алгебраические действия, и типовые замечания к предложенным решениям (типы недочетов A–F перечислены выше)

* задачи могут быть решены альтернативно с использованием аппарата эквивалентных бесконечно малых величин и продублированы в табл. 3.

Примечание: составлена автором на основе данных, полученных в ходе настоящего исследования.

Правильным интеллектуальным приемам принятия решений (таким, как дисциплинированная проверка гипотез с готовностью принять противоположное утверждение в случае выявления противоречия, многошаговые цепочки выводов, декомпозиция, выделение главных факторов, использование классификаций и др.) целесообразно обучаться на материале математики (или, например, юриспруденции – в социальных направлениях подготовки), решая учебные задачи, но ИИ-решатели, как видно, плохо помогают обучиться таким приемам, не разделяя подобные педагогические ценности.

При работе с чуть более сложными ситуациями (задачи 1.7 и 1.8) современные ИИ-решатели могут допускать критические процедурные ошибки (рис. 1).

В табл. 2 представлены задачи, имеющие общее качество: для их решения требуется хорошая эрудиция в области поведения основных элементарных функций, предполагается аргументация при принятии решений с помощью общеизвестных графиков. Нейросетевые решатели не склонны к таким действиям (вместо схематических графиков по специальным запросам могут быть предоставлены элементы Pithon-кода для их построения), поэтому предлагаемые тексты не обладают достаточной наглядностью, цепочки утверждений просто декларируются, часто без уважения к корректному употреблению терминологии (недочет типа B). Некоторые образцы, иллюстрирующие явные недочеты в решениях этих задач, представлены на рис. 2.

Рис. 1. Образцы недочетов к задачам 1.1–1.8 А) Утверждение, не связанное с известными теоремами: разность бесконечно больших величин должна рассматриваться как неопределенность (здесь утверждение оказалось верным из-за небольшой общей степени у двух слагаемых, а при степенях от единицы оно могло оказаться ошибочным). Фактическая ошибка: знаменатель дроби не является бесконечно малой величиной; Б) Для нахождения ответа использован некорректный прием, который годится только для иллюстрации ответа Примечание: составлен авторами по результатам данного исследования

Рис. 2. Образцы недочетов к задачам 2.1–2.5. А) Некорректное утверждение: существование и конечность пределов числителя и знаменателя, при знаменателе, не стремящемся к нулю, надо проверять в соответствии с теоремами; бесконечно большая величина в числителе или знаменателе дроби или бесконечно малая величина в знаменателе дроби тоже не дадут права пользоваться «прямой подстановкой»; Б) Понятийная ошибка: предел действительно не существует, но ожидалось, что заданная функция может быть названа бесконечно большой «по модулю» и результат обозначен «= ∞» без конкретизации знака; В) Понятийная ошибка: неопределенность отсутствует, ситуация подчиняется известным теоремам о связи бесконечно малых и бесконечно больших величин; Г) Некорректное использование терминологии и фактическая ошибка в знаке величины, влекущая общий неверный ответ Примечание: составлен авторами по результатам данного исследования

Таблица 2

Пределы с трансцендентными функциями, предполагающие знание их поведения в разных условиях, и типовые замечания к предложенным решениям (типы недочетов A–F перечислены выше)

Примечание: составлена автором на основе данных, полученных в ходе настоящего исследования.

Таблица 3

Пределы с неопределенностями, требующими применения аппарата эквивалентных бесконечно малых величин или замечательных пределов, и типовые замечания к предложенным решениям (типы недочетов A–F перечислены выше)

* задачи допускают альтернативные решения через элементарные алгебраические преобразования (подбор сопряженных множителей) и продублированы здесь для целей статистического учета замечаний.

Примечание: составлена автором на основе данных, полученных в ходе настоящего исследования.

Рис. 3. Образцы недочетов к задачам 3.1–3.4 А) Некорректное применение «приближенного равенства»; некорректное применение правила Лопиталя (приема, условно недоступного студентам) в неподходящей ситуации, когда неопределенности нет и выражение подчиняется простым теоремам о связи бесконечно больших и бесконечно малых величин; Б) Прием, условно недоступный студентам; В) Неясная фраза Примечание: составлен авторами по результатам данного исследования

Аппарат применения и таблица эквивалентных бесконечно малых величин – эффективный и одновременно доступный инструмент работы с неопределенностями, в которых задействованы трансцендентные функции (табл. 3). К сожалению, нейросетевые решатели практически никогда не угадывают возможность применения этого приема, предлагая в решениях альтернативные частные приемы (качество материала нестабильное), не догадываясь сотрудничать с преподавателем, если последний поставил конкретную учебную цель, а студент не донес ее до запроса. Отсюда происходит современное методическое требование: уделять внимание четкой формулировке учебного задания, подробно оговаривая предполагаемые приемы (и наоборот, нечеткая формулировка задания, а то и скрытый текст задания белым шрифтом на белом фоне, распознаваемый ИИ-решателем, но не студентом, – один из способов выявить факты нежелательного применения технических помощников). Образцы, иллюстрирующие сделанные ошибки, представлены на рис. 3.

Рис. 4. Образцы недочетов к задачам 4.1–4.3 А) Существенно некорректная логика решения; Б) Фактическая ошибка в знаке первого слагаемого, приведшая к неправильному общему результату; В) Неназванные алгебраические или аналитические приемы; ответ не совпадает с декларируемым результатом «разложения» Примечание: составлен авторами по результатам данного исследования

Таблица 4

Другие задачи и типовые замечания к предложенным решениям (типы недочетов A–F перечислены выше)

Примечание: составлена автором на основе данных, полученных в ходе настоящего исследования.

В табл. 4 специально собраны задачи, предполагаемо вызывающие затруднения. Задача 4.1 очень полезная, легко решается с помощью правила Лопиталя (условно недоступного студентам), но ИИ-решатели проявляют свою не лучшую сторону, с самоуверенностью предлагая некорректные идеи. В задачах 4.2 и 4.3 продуктивно можно было бы применить переход линейной заменой к бесконечно малому аргументу, но этот прием ИИ-решатель не увидел (и не использовал никогда во всех рассмотренных задачах). Образцы представлены на рис. 4.

Заключение

Практический аспект работы по нахождению пределов имеет специфику, которую приходится брать во внимание при организации обучения: для нахождения решения всегда требуется сопоставительно использовать разнородную информацию о рассматриваемом аналитическом выражении и об условии предела; часто при поиске решения возникают логические тупики (неопределенности и понимание недостаточной точности принятых ранее решений, выхода на границу областей определения функций и т.п.), требующие возврата к предшествующему состоянию решаемой задачи, когда нужная информация еще не упущена в частных упрощающих действиях. Такой характер учебного материала обуславливает необходимость достаточной интеллектуальной дисциплины у лица, принимающего решения (ЛПР), либо в применении надежных суждений, либо в совершении пробных действий с четким пониманием возможного риска. Нужна некоторая исходная уверенность в своих силах для того, чтобы начать «делать то, что надо» с теми элементами выражения, где это возможно, шаг за шагом (и с готовностью к возвратам, поискам обходных путей) приближаясь к слабо предсказуемому результату.

Кроме того, интуитивная поисковая часть действий, то есть пути от условий и данного к результату, часто оказывается отделенной от процесса оформления решения и остается (в силу психологических эффектов) скрытой не только от конечного читателя предъявленного решения, но и от самого ЛПР, забывающего «неверные ходы» после нахождения правильного пути к ответу.

От удачного учебного текста, в котором рассмотрена конкретная задача на нахождение предела, ожидается не только наличие правильного ответа и обоснование этого ответа, но и вскрытие общих исследовательских установок, внутренней механики получения результата, параллельное аккуратное указание справочных данных и использованных техник решения при фактической корректности. Такие ожидания от решений, предлагаемых нейросетевыми решателями, обученными на текстах сомнительного неконтролируемого качества, были бы явно завышенными, и это не удивительно, что подавляющее большинство предлагаемых решений содержат явные недочеты. Другие особенности предлагаемых решений – полное отсутствие наглядных иллюстраций (графиков основных элементарных функций с акцентированием внимания на нужной зоне) и «суверенное» представление решателей о багаже алгебраических приемов, доступных студентам. Запретить ИИ-решателю использование приемов, изучаемых в учебном курсе позже раздела «Ведение в математический анализ», удается только при специальном составлении запроса. Тем не менее тексты предлагаемых решений принципиально расширяют арсенал учебных текстов (теоретическое изложение темы; справочные материалы; примеры решения аналогичных задач) в аспекте направленности на решение конкретной задачи, это сильная сторона ИИ-решений. Конечно, производительность ЛПР может существенно увеличиться (без отношения к качеству этих работ), но несомненно, что условия пользы нейросетевых решателей связаны с возможностью преодоления недостатков в предлагаемых решениях: желаниями и способностями студентов проводить проверку фактов и процедур, предложенных машиной, сопоставление этих решений с примерами, предложенными в надежных источниках… Педагогическое взаимодействие не упрощается, а «поворачивается» другой стороной, и однозначный прогноз эффектов, вызванных доступностью новых возможностей, затруднителен, так как зависит от множества дополнительных факторов, среди которых особенности понимания «успеха» педагогами и администрацией вуза, накопленная эрудиция, а также неустойчивая и плохо прогнозируемая внутренняя мотивация обучающихся. Сформулируем несколько утверждений, имеющих разнонаправленный характер.

− Студент с доброкачественной ориентацией на продуктивное развитие будет иметь альтернативный инструмент для формулирования первичных идей в индивидуальных работах, однако необходимая критика ИИ-решений, подбор альтернативных к предложенным частным приемам, сопоставление с образцами оформления и другая обработка этих решений может привести к сравнимым затратам времени и усилий; перспективы профессионального становления существенно не меняются.

− Если минимальные учебные требования заключаются в предъявлении студентом какого-нибудь решения задач, это будет происходить легче, как в рамках отдельного раздела, так и в рамках всего курса «Математика», с очевидными негативными последствиями для профессионального становления студента (по сравнению с традиционной траекторией) в дальнейшем: даже ущербная эрудиция (для формирования которой требуется около трех лет систематических учебных усилий в сфере математики) и сниженная мотивация не помешают составлять запросы в соответствии с выданным заданием и предъявлять ответы; коррупционная емкость взаимодействия уменьшится.

− Объективный достоверный контроль учебных достижений студентов станет труднее и дороже; возможные ухудшения собственной фактической обученности инженеров будут частично компенсироваться перманентным использованием технических средств как во время дальнейшего обучения, так и в начале профессиональной деятельности.