Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,279

Введение

Традиционные методы исследования сложных проблем, к которым относятся нелинейные и/или нестационарные задачи медицины, биологии, экологии, стремительно замещаются мультидисциплинарным подходом и растущим числом методов и алгоритмов, их реализующим [1]. Технологии машинного обучения (Machine Learning, ML) [2], извлекая неочевидные закономерности из многомерных наборов данных, способны конструировать наиболее надежный прогноз анализируемых показателей в наборах данных, характерных для биохимических и биофизических систем.

а)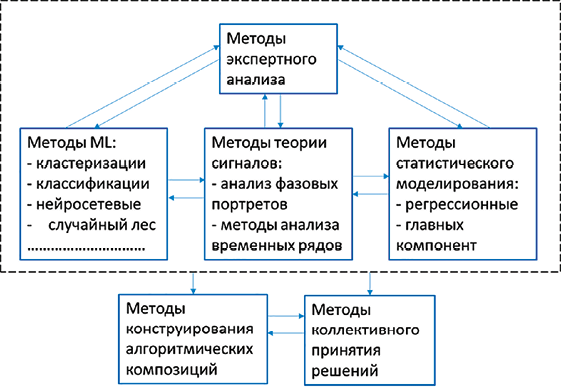

б)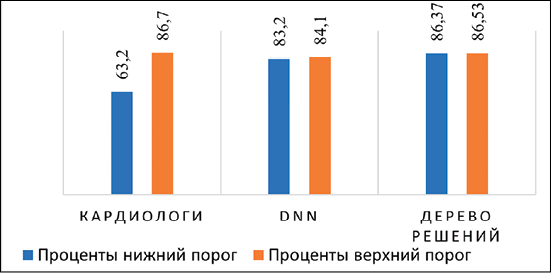

Рис. 1. Современные достижения в анализе ЭКГ-данных: а) основные направления и методы ЭКГ-анализа; б) степень точности определения патологий по ЭКГ Примечание: составлен авторами на основе источников [6–8] для а) и б) соответственно

Современная медицина активно внедряет методы ML (рис. 1, а) для совершенствования диагностики, прогнозирования и лечения заболеваний [3–5]. Одной из ключевых задач в этой области является классификация патологий сердца, играющая важную роль в раннем выявлении сердечно-сосудистых заболеваний, являющихся одной из ведущих причин смертности во всем мире (по данным Всемирной организации здравоохранения).

Однако точность определения патологий сердца при обработке ЭКГ-данных существенно различается у экспертов и алгоритмов [9, 10] (рис. 1, б).

Цель исследования – разработка ансамблевых алгоритмов с эффективностью выше эффективности базовых алгоритмов-операндов и сравнительное исследование ее свойств на выборке ограниченного объема первичных данных в открытом доступе.

Материалы и методы исследования

Полагаем, что диагностируемый набор исходных данных как сведения о некотором динамическом объекте в форме фрагментов временных рядов, порожденных случайным процессом:

, (*)

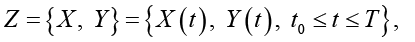
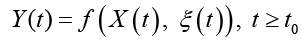характеризующим состояние исследуемого объекта и принимающего значения в фазовом пространстве с σ-алгеброй подмножеств пространства, покрывающей всевозможные физические ситуации. При этом X(t) сопоставлен ненаблюдаемым (истинным) переменным состояния системы; Y(t) – случайная наблюдаемая функция; ξ(t) – неизвестный шум с ограниченной дисперсией. Относительно модели (*) на [t0, Т] выдвинуто n > 0 гипотез (диагнозов) (Ω1,…,Ωn), составляющих полную группу событий. Полагаем, что фрагмент реализации процесса (*) может принадлежать только одному из классов 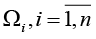. Измерения Y(t) осуществляются по дискретному плану 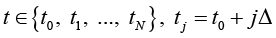, 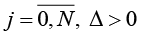. Задача состоит в построении решающего правила, относящего наблюдаемый фрагмент реализации случайного процесса Y(t) (*) к одному из классов 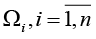и оценивании его качества в смысле заданных критериев.

В рамках описания (*) конструирование ансамбля моделей, в котором базовые алгоритмы кооперируются для получения более эффективного решения за счет взаимного парирования ошибок отдельных алгоритмов, осуществляем на основе ML.

В качестве базовых алгоритмов рассмотрим наиболее популярные [11]: метод опорных векторов (SVM), деревья решений, метод k-ближайших соседей (KNN), наивный байесовский алгоритм (Naive Bayes (NB)).

К общепринятым метрикам оценки эффективности алгоритмов машинного обучения [12] относят: Recall, Precision и F1-Score, оценивающие, в частности, ошибки 1, 2 родов (частоту ложноположительных и ложноотрицательных случаев, табл. 1), а также кривую ROC (Receiver Operating Characteristic), площадь под ней ROC-AUC (Area Under the ROC Curve).

Таблица 1

Матрица ошибок (Confusion Matrix) [13]

Описание условий эксперимента и результаты численного моделирования четырех базовых алгоритмов. На основе данных [13] сформирована выборка из 812 записей (360 двухсекундных фрагментов ЭКГ как признаков), сопоставленных четырем классам нарушений сердечного ритма: 1) опасные для жизни аритмии, требующие неотложной реанимации (трепетание желудочков; фибрилляция желудочков); 2) опасные для жизни желудочковые аритмии (желудочковая тахикардия высокой частоты: мономорфная и полиморфная); 3) суправентрикулярные аритмии (мерцательная аритмия, наджелудочковая тахикардия, синусовая брадикардия, блокада сердца первой степени, узловой ритм); 4) нормальный синусовый ритм с объемами выборок, равными 337, 169, 106, 200 записей соответственно.

Ансамбли алгоритмов. Конструирование ансамблевых алгоритмов осуществляется попарным стекингом в форме метамодели с целью получения более совершенной модели, которая будет содержать суперпозицию операндов – комбинируемых алгоритмов. В качестве метамодели использовалась логистическая регрессия, в которой в отличие от линейной свертки голосов алгоритмов с фиксированными коэффициентами используется более сложная стратегия алгоритмической суперпозиции, выявляющая неочевидные взаимосвязи и контекстные зависимости между алгоритмами, динамически определяя, предсказания какого алгоритма заслуживают большего доверия в текущих условиях (например, [2, 14, 15]).

Результаты исследования и их обсуждение

Реализация алгоритмов (рис. 2–7, табл. 2–4) производилась на языке Python 3.11+ с применением библиотек Pandas 2.2.3, NumPy 2.0.2, Scipy 1.13.1, Matplotlib 3.9.4, Scirit-Learn и модулей Time, Os; ссылка на веб-сервис GitHub с полным кодом проекта https://github.com/NikosSoRf/stat.git.

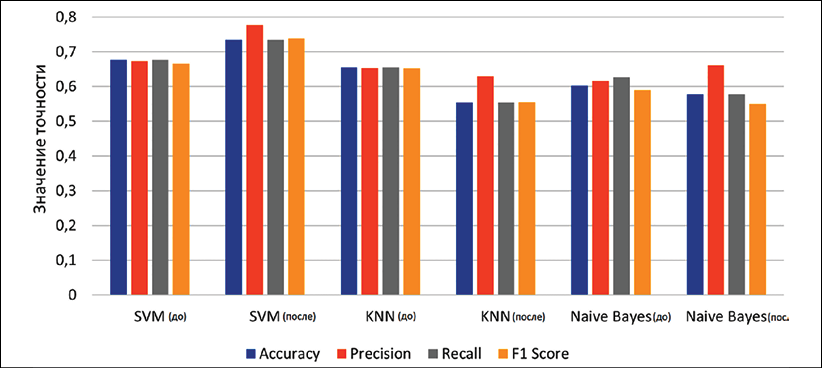
Рис. 2. Сравнительная диаграмма метрик алгоритмов до и после балансировки (устранение дисбаланса классов до 106 записей, метод Random Undersampling) Примечание: составлен авторами по результатам данного исследования

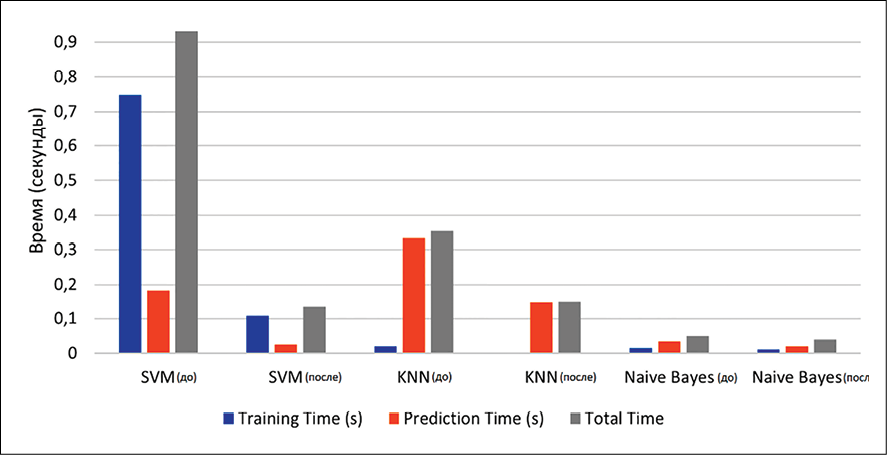
Рис. 3. Результат сравнения времени работы алгоритмов до и после балансировки Примечание: составлен авторами по результатам данного исследования

Таблица 2

Результаты сравнения свойств базовых алгоритмов для неравномерного и равномерного наборов ( / )

Примечание: составлена авторами на основе полученных данных в ходе исследования.

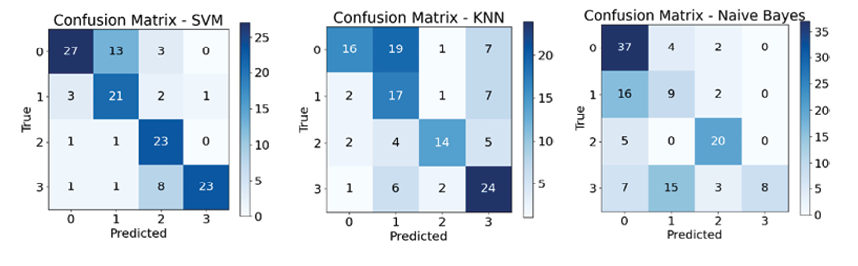
Рис. 4. Матрицы ошибок алгоритмов в условиях равномерного распределения объектов римечание: составлен авторами по результатам данного исследования

Подбор параметров осуществлен методом GridSearch, диапазоны рассматриваемых параметров GridSearch: для SVM C: [0.1, 1, 10, 100], kernel: [‘linear’, ‘rbf’, ‘poly’], gamma: [‘scale’, ‘auto’, 0.1, 0.01], для KNN n_neighbors: [3, 5, 7, 9, 11], weights: [‘uniform’, ‘distance’], metric: [‘euclidean’, ‘manhattan’, ‘minkowski’]; для SVM – радиальная функция с параметрами C = 40, gamma = 0.1; для KNN k = 5; p = 2 для L2 нормы, weights = uniform; для NB параметр сглаживания 10- 6. Оценка качества модели осуществлялась на основе кросс-валидации (30 и 70 % от исходного объема на тестовую и обучающую выборки) с использованием out-of-fold в методе cross_val_predict (см. текст программы https://github.com/NikosSoRf/stat.git). В связи с ограниченным объемом сбалансированной выборки (106 наблюдений, 4 класса) для оценки стабильности модели применена 10-кратная стратифицированная кросс-валидация.

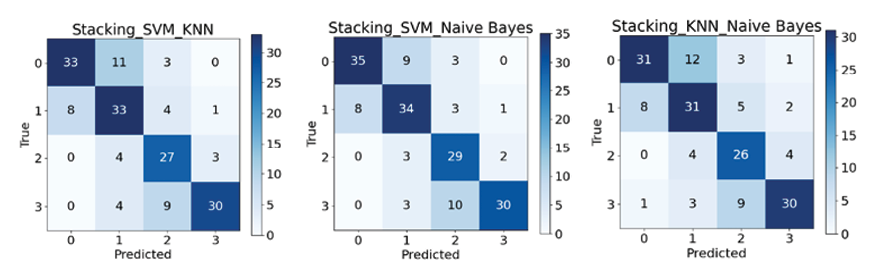
Рис. 5. Матрицы ошибок ансамблей алгоритмов Примечание: составлен авторами по результатам данного исследования

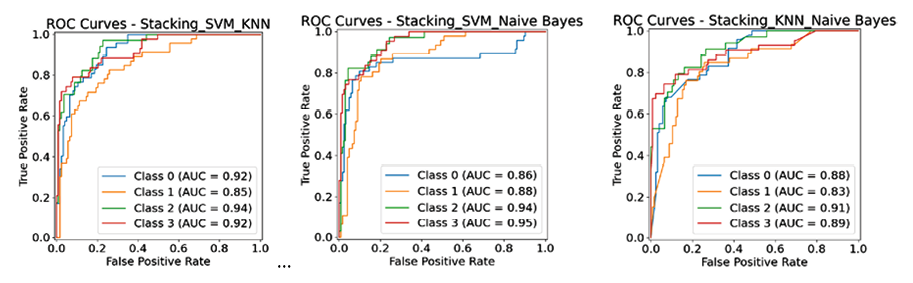
Рис. 6. Графики ROC кривых для ансамблевых алгоритмов Примечание: составлен авторами по результатам данного исследования

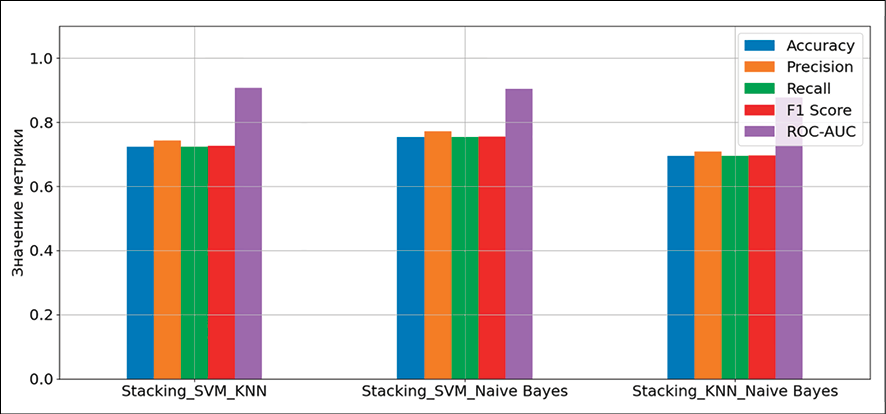
Рис. 7. Сравнительные диаграммы метрик точности ансамблевых алгоритмов Примечание: составлен авторами по результатам данного исследования

Таблица 3

Результаты сравнения ансамблей алгоритмов до и после аугментации ( / )

Примечание: составлена авторами на основе полученных данных в ходе исследования.

Таблица 4

Статистические показатели для средней точности предсказания с уровнем значимости p = 0,05

Примечание: составлена авторами на основе полученных данных в ходе исследования

Из рис. 4 и 5 следует явное преимущество ансамблевых методов перед отдельными алгоритмами, при этом благодаря некоррелированности ошибок базовых алгоритмов (SVM, KNN, NB) их комбинация не только повышает общую точность, но и значительно улучшает сбалансированные метрики для слабо определяемых классов, обеспечив более надежную и устойчивую диагностическую систему.

Ансамбль SVM-NB (рис. 7) демонстрирует самую высокую и стабильную производительность по большинству классов, достигнут лучший результат по 0-му классу (опасные для жизни аритмии) и имеет место определенный баланс результатов относительно других классов. Ансамбль SVM-KNN является менее уверенным и стабильным из рассмотренных с самым низким значением у 0-го класса, а ансамбль KNN-NB оказался наименее эффективным без явных преимуществ перед соперниками, по всем классам есть пары, которые показывают равный или лучший результат (рис. 6, 7; табл. 3).

Из табл. 3 следует, что ансамбль SVM-NB достигает наивысших значений по ключевым метрикам Accuracy (табл. 4), Precision, Recall и F1-Score, при этом его общее время выполнения остается конкурентоспособным.

Ансамбль SVM-KNN показывает очень близкий результат по ROC-AUC (0.907) и является самым быстрым среди коллективов с SVM. В свою очередь, ансамбль KNN-NB, несмотря на рекордную скорость работы (0,042 с), существенно уступает конкурентам по всем метрикам точности, что не позволяет считать его эффективным для данной задачи.

Аугментация выборки на основе метода Smoothing привела к увеличению размера данных в 2 раза (до 848 записей, по 212 на класс) и ожидаемо к улучшению результатов (после дробной черты в табл. 3). При этом тестирование проходило на нескольких методах аугментации: noising, scaling, smoothing. Метод с шумом не показал существенно лучших результатов, но сильно увеличил время обработки данных.

Из табл. 3 следует, что точность ансамблевых алгоритмов возросла, но увеличились временные затраты на обучение (почти в 2 раза у каждой модели) и ответа алгоритмов (на 0,04 с у моделей с SVM и в 3 раза у моделей без SVM в условиях ниже приведенных параметров вычислительного устройства).

Эксперименты проводились на основе операционной системы Windows 10; аппаратная конфигурация включала процессор Intel Core i3-5005U (2,00 GHz), 8 ГБ оперативной памяти DDR3 и интегрированную графику Intel HD Graphics 5500. Внешние Python-библиотеки, необходимые для работы проекта, представлены в файле requirements.txt.

Заключение

В статье представлены результаты сравнительного анализа наиболее часто используемых алгоритмов машинного обучения для задачи четырехмерной классификации патологий сердца на первичных данных в условиях ограниченного объема выборки. Результаты данной работы могут быть полезны при разработке веб-сервиса для апробации потоковой диагностики по ограниченным данным. Дальнейшее развитие в этом направлении авторы связывают с параллельным решением следующих задач: 1) разработка масштабируемой проблемно-ориентированной программной системы для иерархического поиска эффективных композиций и ансамблевых алгоритмов на большом наборе данных; 2) создание метамодели коллектива алгоритмов, обучающейся на разнотипных данных.