Введение
Электролитные системы все активнее внедряются в современные технологические процессы. Они являются ключевым компонентом в таких направлениях, как создание проточных редокс-батарей, разработка плазменно-электролитных методов обработки материалов и производство металлических порошков для последующего использования в аддитивных технологиях [1–3].
Моделирование электролиза невозможно без анализа реакций на электродных поверхностях. Тип и механизм этих электрохимических процессов напрямую зависят от кислотности среды (pH). При этом итоговые реакции, фигурирующие в моделях, представляют собой обобщение многостадийных превращений.
Важно понимать, что общая запись суммарной реакции электролиза объединяет два пространственно разделенных процесса: анодное окисление и катодное восстановление, протекающие на разных электродах. К примеру, механизм адсорбции водорода на инертных металлах различен для сред с разной кислотностью. В кислых растворах этот процесс описывается реакцией 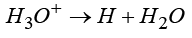 , тогда как в щелочных средах он протекает согласно
, тогда как в щелочных средах он протекает согласно 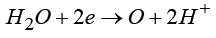 .
.
Для формулировки граничных условий в электрохимических задачах широко применяется закон Фарадея:
m = (Q / F) * (M / z).
В данном уравнении m представляет массу вещества, осажденного на электроде, параметр M/z соответствует эквивалентной массе продукта реакции, Q – суммарный электрический заряд, F – постоянную Фарадея. Следует отметить, что в реальных экспериментах наблюдаемое количество полученного вещества, как правило, отличается от теоретического значения, предсказанного законом Фарадея [4]. Причиной данного несоответствия является идеализированная природа закона Фарадея, предполагающая протекание лишь одной электрохимической реакции. На практике же выход меди может быть снижен до 98–99 % из-за параллельности процессов восстановления одно- и двухвалентных ионов меди [5]. Таким образом, характеристика, равная соотношению практического выхода к теоретическому, получила название «выход по току» [6].
Для описания зависимости скорости электродной реакции от потенциала используется уравнение Батлера – Фольмера. Данное уравнение непосредственно связывает величину тока, протекающего через электрод, с его перенапряжением и фундаментальными кинетическими константами стадий окисления и восстановления.
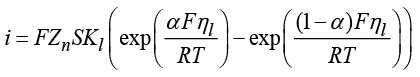 .
.
где i – плотность тока, ηl – перенапряжение электродной реакции на электроде l, S – площадь электродов, Zn – величина валентности, α – экспериментальный параметр, характеризующий перенос частиц между электродами.
Уравнение анодно-катодной волны также используется при описании граничных условий:
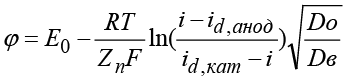 ,
,
где Do, Dв – коэффициенты диффузии окисленной и восстановленной форм, 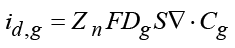 – диффузионный ток, φ – потенциал электродов, R – универсальная газовая постоянная, T – температура электролита.
– диффузионный ток, φ – потенциал электродов, R – универсальная газовая постоянная, T – температура электролита.
Поляризационные кривые наиболее информативны для многокомпонентных растворов, в которых несколько электроактивных веществ выделяются поэтапно. Моделирование таких систем основано на решении системы кинетических уравнений, где константы скоростей обычно задаются через закон Аррениуса. Тем не менее данный подход не всегда универсален, так как отдельные стадии электролиза могут иметь различный порядок и не подчиняться аррениусовской зависимости [7]. Моделирование требует корректного выбора математического аппарата. Со стороны кинетики закон Аррениуса применим лишь тогда, когда лимитирующая стадия не является гетерогенной диссоциацией. Со стороны электростатики для определения конфигурации электрического поля применяют либо уравнение Пуассона, либо его приближение в виде условия локальной электронейтральности [8; 9]. На стенках часто ставят нормальную компоненту равной нулю (уравнение неразрывности) [10; 11]. Потенциал и перенапряжение, используемые для описания граничных условий, характеризуют именно электрохимические реакции, а не материал электрода [9; 12]. Современное понимание процессов описано в [13; 14]. При построении модели граничные условия для уравнения Пуассона на поверхности электрода часто формулируются на основе эмпирических данных. Ключевым инструментом для получения таких данных и изучения механизмов реакций служит анализ поляризационных кривых, графически отображающих зависимость тока от электродного потенциала.
Таким образом, прямое использование рассмотренных законов при постановке граничных условий для математической модели сопряжено с рядом фундаментальных трудностей. Одни из них оперируют интегральными параметрами, объединяющими вклад обоих электродов, другие содержат эмпирические подгоночные коэффициенты, а третьи применимы исключительно для лимитирующей стадии, что не отражает всей сложности многостадийного процесса. Как следствие, их использование в модели неизбежно ведет к одному из двух сценариев: либо к появлению дополнительных подгоночных параметров, требующих экспериментального определения для каждой конкретной системы, либо к ограничению области применимости модели лишь теми техническими условиями, которые были всесторонне изучены эмпирическим путем.
Цель исследования – разработка алгоритмического обеспечения для расчета констант скоростей электродных реакций с последующей имплементацией в математическую модель.
Материалы и методы исследования
Объектом численного исследования выступает щелочной раствор KOH. Данный электролит взят как одно из недорогих возможных решений для получения водорода на этапе перехода к «зеленой энергетике» [15]. Использование недорогих щелочных электролитов в будущем позволит снизить общие затраты на производство водорода, делая технологию более масштабируемой и привлекательной для широкого внедрения.
Моделирование электролиза в гетерогенной системе между плоско-параллельными инертными электродами при допущении о потенциальности электрического поля реализовано в виде системы уравнений, содержащей:
1. Основу модели составляют начально-краевые задачи для уравнений переноса (диффузии-конвекции), определяющих пространственно-временное распределение концентраций ионных компонентов. Конкретный набор уравнений зависит от состава электролита. При моделировании электролиза КОН система включает уравнения переноса для гидроксид-ионов, катионов водорода и катионов калия.
2. Краевая задача для потенциала электрического поля.
Для математического представления модели примем, что катод расположен при x = 0, анод при x = b, и введем следующие обозначения:
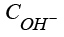 ,
, 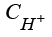 ,
, 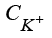 ,
, 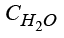 – концентрации гидроксильной группы, катионов водорода и калия, воды;
– концентрации гидроксильной группы, катионов водорода и калия, воды;
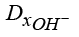 ,
, 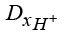 ,
, 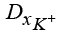 – коэффициенты диффузии гидроксильной группы, катионов водорода и калия;
– коэффициенты диффузии гидроксильной группы, катионов водорода и калия;
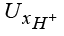 ,
, 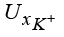 – значения подвижности гидроксильной группы, катионов водорода и калия;
– значения подвижности гидроксильной группы, катионов водорода и калия;
ℜ – константа скорости процесса диссоциации воды,
χ – электрическая восприимчивость электролита,
ε0 – диэлектрическая постоянная,
k1, k2, k3, k4 – константы скоростей катодных процессов
(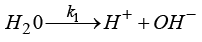 ,
,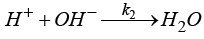 ,
,
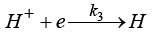 ,
, 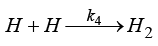 ),
),
l1, l2, l3, l4 – анодных в щелочном электролите
(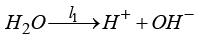 ,
, 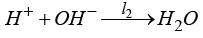 ,
,
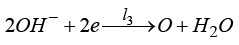 ,
, 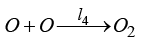 ).
).
Таким образом, компоненты математической модели:
1) Уравнение баланса аниона OH– с граничными условиями:
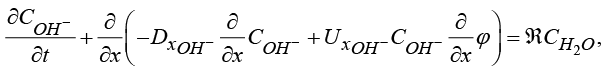 (1)
(1)
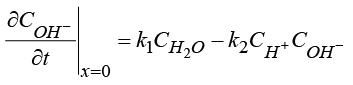 , (2)
, (2)
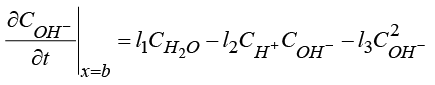 . (3)
. (3)
2) Уравнение баланса катиона H+ с граничными условиями:
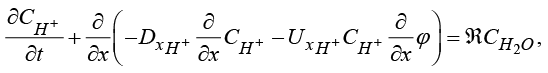 (4)
(4)
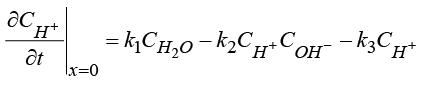 , (5)
, (5)
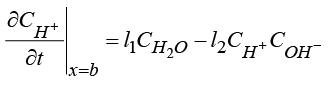 . (6)
. (6)
3) Уравнение баланса катиона K+ с граничными условиями:
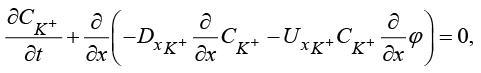 (7)
(7)
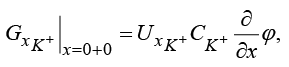 (8)
(8)
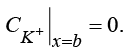 (9)
(9)
4) Уравнение Пуассона для потенциала электрического поля
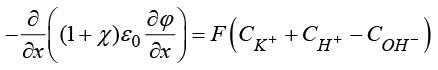 , (10)
, (10)
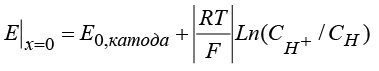 , (11)
, (11)
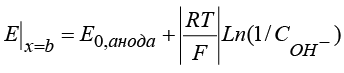 . (12)
. (12)
При вычислении перенапряжения учитываются только концентрации частиц, реагирующих на рассматриваемом электроде (аноде или катоде). Для определения концентрации частиц, принимающих участие в окислительно-восстановительных реакциях на электродах, и количества вещества, сформировавшегося на электроде, также решаются системы, состоящие из задач Коши, описывающих стадийные электрохимические реакции:
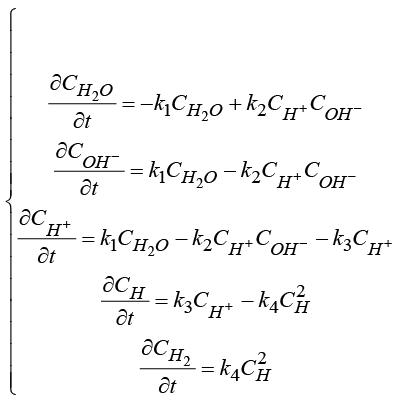 (13)
(13)
И выход кислорода (анод):
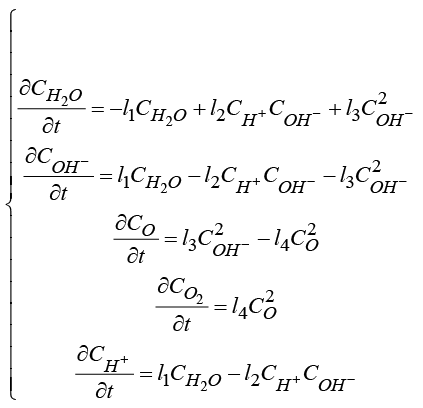 (14)
(14)
Указанная модель предназначена для описания пространственной неоднородности внутренних параметров гетерогенных систем в области между электродами.
Вычислительный алгоритм реализует поэтапное решение начально-краевых задач. Для их дискретизации на равномерной пространственной сетке интегро-интерполяционным методом строятся явные разностные схемы. Все коэффициенты системы рассчитываются на нижнем временном слое. Переход между временными слоями организован следующим образом: при заданном общем шаге по времени для каждой задачи проверяется условие Куранта. Если рассчитанный из этого условия локальный шаг оказывается меньше общего, то переход к следующему основному слою осуществляется через серию промежуточных шагов, соответствующих критерию устойчивости. Решение уравнения Пуассона выполняется на заключительном этапе с использованием рассчитанных концентраций частиц на новом временном слое.
В качестве начальных условий принимается равномерное распределение концентраций по всему объему электролита. Цепочки стадийных электрохимических реакций содержат в себе как гетерогенные реакции, то есть реакции нулевого порядка, проходящие на электроде, так реакции между их продуктами. Учитывая, что кинетические константы являются заранее неопределёнными параметрами и зависят от конкретных условий системы, на первом этапе проводится их оценка. Данная процедура основана на решении обратной нульмерной задачи, подробно описанной в литературе [16; 17].
Результаты исследования и их обсуждение
Разработанный численный алгоритм обеспечивает прогнозирование выхода водорода, определение констант скоростей электродных процессов по экспериментальным данным о выходе продукта, а также расчет пространственно-временных распределений концентраций реагентов в приэлектродных областях. Поставленная модель не связывает напрямую оба электрода изначально при ее построении, что дает возможность перехода к технологиям, разрабатываемым на основе фундаментальных основ процесса электролиза, но затрудненным для экспериментального исследования, например разряды с жидкими электродами, где нет возможности промерить напряжение на границе раздела электролит – рабочий газ [1; 3]. Верифицировался алгоритм по данным с электролизера конфигурацией: 50 мм – внутренний диаметр, 60 см2 – рабочая площадь электродов, 300 мм – высота уровня электролита, электролит – это 30 % раствор KOH [7]. Значения коэффициентов диффузии, подвижности ионов, диэлектрическая проницаемость взяты согласно значениям приведенным в [18, с. 23, 31, 39, 49], константа диссоциация воды [19]. Температуру, поддерживаемую постоянной с помощью регулирующего потенциометра, берем согласно данным, приведенным в [7]. В целом расчеты показали хорошее совпадение расчетных и экспериментальных данных, расхождения не превышают 11 %. На рис. 1 представлено сравнение экспериментальных и расчетных данных при 0,5 А и 60°C при катодном выделении водорода.
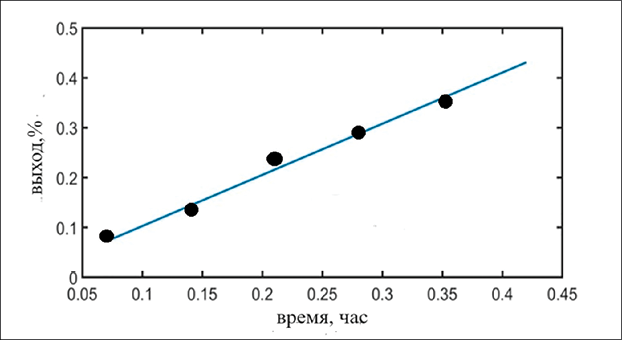
Рис. 1. Выход водорода (0,5 А и 60 °C). Точки – результаты эксперимента работы [7], прямая представляет расчетные данные данного исследования
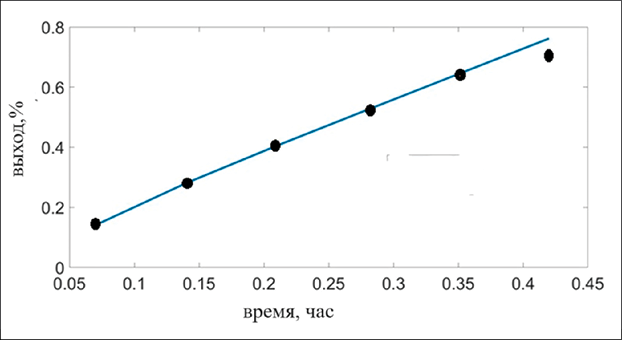
Рис. 2. Выход кислорода (1 А и 80 °C). Точки – результаты эксперимента работы [7], прямая представляет расчетные данные данного исследования
На рис. 2 отображено анодное выделение кислорода при 1 А и 80 °C. Для сравнения взяты эксперименты работы [7].
Проведенные расчеты показали, что в приближении постоянной поверхности электрода (при выделении газообразных продуктов) погрешность определения выхода газа несущественно отличается от результатов нульмерной модели, однако вычислительные затраты при этом возросли. Однако обоснованность необходимости решения пространственной задачи возникает при расчете задачи с изменением активной поверхности электрода вследствие образования на нем поверхностных покрытий [20]. Разработанные алгоритмы легли в основу программного обеспечения [21].
Заключение
Предложен алгоритм численного решения одномерной задачи, учитывающий кинетику процессов на межфазной границе электрод – электролит. Многостадийность электрохимических реакций выделения веществ моделируется с помощью систем кинетических уравнений. Для решения задач химической кинетики применяются методы Рунге – Кутты, эффективные для прямых расчетов при известных константах скоростей. В случае неизвестных кинетических параметров требуется решение обратных оптимизационных задач. В данной работе представлен алгоритм для одномерного случая, состоящий из двух независимых блоков. Первый блок решает нульмерную задачу идентификации констант скоростей электрохимических процессов.
Решение кинетических задач позволяет количественно оценить вклад отдельных приэлектродных процессов и выполнить предварительный прогноз газовыделения. Второй блок алгоритма реализует решение поставленной математической модели нахождения пространственных характеристик. Сравнение расчетных и экспериментальных данных показало хорошее количественное совпадение по объему выделенного газа на обоих электродах. Анализ пространственных распределений продемонстрировал качественное соответствие, выражающееся в воспроизведении характерных градиентов концентраций.



