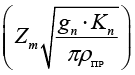Введение
Известно, что для разработки современных машин требуются глобоидно-цилиндрические червячные приводы, позволяющие обеспечить высокую нагрузочную способность, коэффициент полезного действия (КПД), ресурс работы, а также при этом обладающие малым весом и габаритами [1].
Для реализации конструкторско-технологических решений, обеспечивающих повышение нагрузочной способности глобоидно-цилиндрической червячной пары с вогнутой формой винтовой поверхности червяка и выпуклой формой зубьев сопряженного колеса приводов, требуется разработать новые научно обоснованные подходы к геометрическим принципам образования рабочих поверхностей сопряженных пар, а также методам их изготовления и контроля. Реализация научно обоснованных подходов может позволить устранить имеющие технологические недостатки изготовления профильно сопряженных глобоидных передач, обусловленных низкой производительностью и высокой трудоемкостью нарезания вогнутой винтовой поверхности глобоидного червяка [2, с. 212-214].
На сегодняшний день схему образования зацепления модернизированной классической глобоидной передачи, как правило, формируют путём получения производящей образующей линии методом копирования рабочей поверхности инструмента в процессе нарезания винтовой поверхности (ВП) глобоидного линейчатого червяка. Передачи глобоидные с линейчатым червяком в настоящее время широко применяются в промышленности, однако они имеют недостатки по нагрузочной способности по сравнению с профильно сопряженными червячными передачами [3, с. 386-390]. При ротационном точении винтовой поверхности (ВП) глобоидного нелинейчатого червяка с вогнутым эвольвентным профилем производящую образующую линию формируют по схеме обкатки с профилированием методом огибания. Выполнение нарезания витков указанного червяка многолезвийным принудительно вращаемым инструментом в режиме обкатки обеспечивает получение сложнопрофильной поверхности с высокой точностью (до 7-й степени) и пониженной шероховатостью (Ra ≈ 2,2–2,9 мкм) относительно обработки одиночным резцом. При этом процесс нарезания ВП ротационным точением в 16 раз превышает по производительности изготовление глобоидного червяка трехрезцовой головкой [4].
Изготовление зубьев сопряженного цилиндрического колеса цилиндрической червячной фрезой позволяет отказаться от глобоидной червячной фрезы, что снижает затраты на режущий инструмент. При проектировании и изготовлении профильно сопряженных глобоидных передач необходима разработка методики образования выпукло-вогнутого поверхностного зацепления глобоидно-цилиндрической червячной пары для реализации поверхностного контакта, обеспечивающего более низкое напряжение. Низкое контактное напряжение даст возможность повысить нагрузочную способность профильно сопряженной червячной пары [5, с. 144-152], снизить габариты и массу, а также увеличить ресурс работы и КПД. Нагрузочная способность может быть увеличена в 1,4-3 раза, КПД на 10-30%, ресурс работы в 2-3 раза по сравнению с существующими передачами.
Целью исследования является разработка методики образования зацепления радиусно-сопряженной глобоидно-цилиндрической пары привода с нелинейчатым червяком, профиль витка которого очерчен по вогнутой эвольвенте, а зубьев сопряженного колеса – по выпуклой эвольвенте.
Материалы и методы исследования
В работах приведен анализ особенностей технологий изготовления глобоидно-цилиндрических передач [5, с. 280-286; 6; 7]. Показаны технологические сложности нарезания ВП глобоидного червяка с вогнутым эвольвентным профилем, позволяющим обеспечить повышение радиуса приведенной кривизны в зацеплении глобоидно-цилиндрической пары. Увеличение радиуса приведенной кривизны в зацеплении способствует повышению пятна поверхностного контакта рабочих поверхностей и снижению контактного напряжения [4; 5, с. 120-124]. Для изготовления глобоидного червяка с вогнутым эвольвентным профилем предложен метод ротационного точения (РТ) [8]. Оценить радиусный профиль ВП глобоидного червяка и зубьев сопряженного колеса позволяет разработанная модель глобоидного червяка с вогнутым эвольвентным профилем винтовой поверхности и сопряженного с ним цилиндрического колеса с выпуклым эвольвентным профилем зубьев [9, с. 10-45]. Представлены формулы [10] для расчета контактного и изгибочного напряжения, учитывающие влияние радиуса приведенной кривизны в зацеплении на их значения с учетом формулы Герца [9, с. 10-45; 11; 12].
Предложено радиус приведенной кривизны в зацеплении определить на основе радиуса приведенной кривизны профиля зуба червячного колеса, взятого как исходное формообразующее звено. Радиус кривизны глобоидного червяка определяется через предложенный коэффициент (Кс) сопряжения радиусных рабочих поверхностей, устанавливаемый на основе графика зависимости коэффициента контактного напряжения Кδn. Представлен аналитический анализ и формулы [12, с. 386-394] для расчета радиусов кривизны зуба сопряженного цилиндрического колеса и глобоидного червяка с ВП вогнутого эвольвентного профиля, а также приведенного радиуса кривизны в зацеплении. На основе аналитических и экспериментальных методов разработана методика образования зацепления профильно сопряженной глобоидно-цилиндрической червячной пары с применением коэффициента снижения контактного напряжения, путем сравнения его с контактным напряжением глобоидно-цилиндрической червячной пары с линейчатым червяком.
Результаты исследования и их обсуждение
C целью проведения исследований была разработана модель глобоидного червяка с вогнутым эвольвентным профилем винтовой поверхности и сопряженного с ним цилиндрического глобоидного колеса с выпуклым эвольвентным профилем зубьев, которая представлена на рисунке 1.
Моделирование позволяет оценить радиусный профиль ВП глобоидного червяка и зубьев цилиндрического прямозубого колеса, а также возможного их профильного сопряжения [7, с. 10-45; 13].
Для опытной глобоидно-цилиндрической червячной пары был проведен геометрический расчет [3, с. 98-110], а также расчет на прочность на основе определения контактных и изгибочных напряжений при условии, когда червяк линейчатый. Контактное напряжение δn рассчитывалось по формуле [10]:
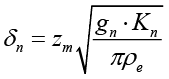, (1)
где Zm – коэффициент, учитывающий механические свойства материалов, gn – удельная нормальная нагрузка, Кn – коэффициент нагрузки по контактным напряжениям, ρе – приведенный радиус кривизны контактных поверхностей.
Радиус приведенной кривизны лежит в основе определения контактных напряжений δn, чем выше радиус приведенной кривизны, тем меньше контактные напряжения. Это характерно, когда глобоидный червяк имеет ВП нелинейчатого профиля.
Изгибочное напряжение зубьев зубчатого колеса, сопряженного с глобоидным червяком, рассчитывалось по формуле [10]:
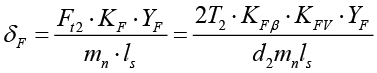, (2)
где KF – коэффициент нагрузки при изгибе, KFβ – коэффициент концентрации нагрузки при изгибе, KFV – коэффициент динамической нагрузки при изгибе, mn – нормальный модуль, YF – коэффициент формы зуба, T2 – крутящий момент, Ft2 – окружное усилие на червячном колесе, ls – суммарная длина контактных линий, d2 – делительный диаметр колеса.
Суммарная длина контактных линий с увеличением радиуса приведенной кривизны тоже увеличивается и способствует увеличению пятна контакта [14], что позволяет снизить изгибочное напряжение, действующего на зуб колеса, сопряженного с ВП глобоидного червяка.
Рис. 1. Разработка моделей для исследований: а) модель глобоидного червяка с эвольвентным вогнутым профилем винтовой поверхности; б) модель цилиндрического прямозубого колеса с выпуклым эвольвентным профилем зубьев Источник: составлено авторами
Известно, что увеличение радиуса приведенной кривизны ведет к снижению контактных напряжений в зацеплении глобоидной передачи в соответствии с формулой Герца [12]. Радиус приведенной кривизны зависит от вида сопряжения контактирующих поверхностей червячной пары. Виды контактирующих поверхностей червячной пары представлены на рисунке 2 (а и б).
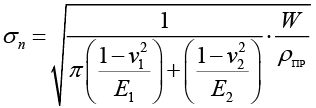, (3)
где v1, v2, Е1, Е2 – модули упругости и коэффициенты Пуассона материалов червячной пары, ρпр – приведенный радиус кривизны, W – нормальная нагрузка на единицу длины контактной линии.
Радиус приведенной кривизны ρпр1 червячной пары, при условии, что червяк линейчатый (рис. 2б), определялся по радиусу кривизны профиля зуба червячного колеса:
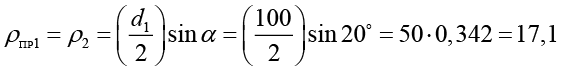мм, (4)
где d1 – делительный диаметр червячного колеса, d1=100 мм;
α = 20° – угол зуба в средней плоскости колеса.
Если профиль червяка нелинейчатый (рис. 2а), то радиус приведенной кривизны ρпр2 сопряженных криволинейных поверхностей рассчитывается по формуле Герца:
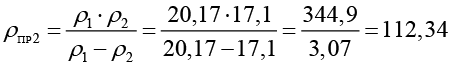мм, (5)
где ρ1 – радиус кривизны глобоидного червяка.
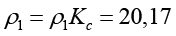мм, (6)
где Кс – коэффициент сопряжения радиусных поверхностей; Кс = 1,18.
Коэффициент снижения контактного напряжения Кδn в зацеплении составил 2,56 раза за счет увеличения ρпр2, Кδn рассчитывался по формуле:
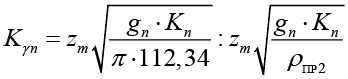(7)
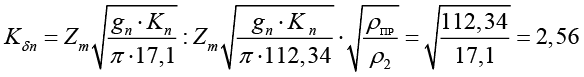, (8)
где Zm – коэффициент, учитывающий механические свойства материалов;
gn – удельная нормальная нагрузка;
Кn – коэффициент нагрузки по контактным напряжениям;
ρe – приведенный радиус кривизны контактных поверхностей.
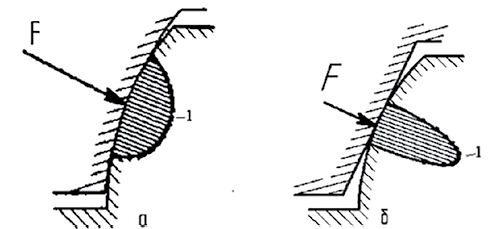
Рис. 2. Виды контактирующих поверхностей червячной пары: а) выпукло-вогнутые контактирующие поверхности глобоидно-цилиндрической червячной пары; б) линейный контакт рабочих поверхностей цилиндрической червячной пары; 1) распределение напряжения в зоне зацепления Источник: составлено авторами
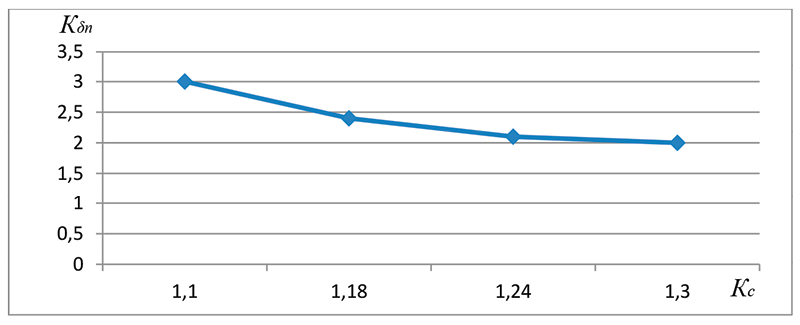
Рис. 3. Зависимость коэффициента снижения контактного напряжения Кδn от коэффициента Кс сопряжения радиусных рабочих поверхностей в зацеплении червячной передачи
Методика образования зацепления профильно сопряженной глобоидной червячной пары
|
№п/п |
Наименование этапа |
Примечание |
|
1 |
Расчет геометрических размеров глобоидной червячной пары и прочностных параметров |
Формулы в [8] |
|
2 |
Определение радиуса кривизны ρ2 профиля зуба цилиндрического колеса в зацеплении |
|
|
3 |
Определение радиуса кривизны ρ1 профиля витков глобоидного червяка в зацеплении |
|
|
4 |
По формуле Герца рассчитать радиус приведенной кривизны сопряженной глобоидной червячной пары |
|
|
5 |
Определить коэффициент снижения контактного напряжения Кδn в зацеплении за счет увеличения радиуса приведенной кривизны по сравнению с зацеплением с линейчатым червяком, когда ρПР = ρ2 |
|
|
6 |
Рассчитать на прочность глобоидную червячную пару |
Формулы в [7, с. 10-45] |
|
7 |
Изготовить профильно сопряженную червячную пару |
Технологические схемы [5, с. 240-251] |
:
График зависимости коэффициента снижения контактного напряжения Кδn от коэффициента Кс сопряжения радиусных рабочих поверхностей в зацеплении глобоидно-цилиндрической червячной передачи показан на рисунке 3, который разработан авторами.
На основании расчета геометрических и прочностных параметров, а также экспериментальных исследований разработана методика образования зацепления опытной профильно сопряженной червячной пары с нелинейчатым червяком (таблица) [15].
Разработанная методика образования зацепления профильно сопряженной глобоидной червячной пары может быть использована при проектировании и изготовлении глобоидно-цилиндрических передач.
Заключение
Критический анализ и систематизация материалов по решению научно-технологических задач оптимизации геометрии зацепления, направленных на снижение контактных напряжений при увеличении приведенного радиуса кривизны и длины контактных линий, выявили сложность технологических проблем. Проблемные вопросы, связанные с технологией изготовления глобоидных червячных передач радиусного сопряженного профиля, применяемых для создания перспективных профильно сопряженных приводов, рассмотрены на основе работ известных ученых в области разработок геометрии зацепления и технологии изготовления глобоидных червячных передач.
Ключевая идея исследований, ориентированных на повышение эксплуатационных характеристик классических глобоидных передач с линейчатым червяком, состоит в обеспечении такой геометрии зацепления, которая оптимально формируется в процессе установившейся работы червячного редуктора. С опорой на обширный массив теоретических и экспериментальных данных были усовершенствованы методики проектирования и технологии изготовления классических глобоидных передач. В частности, предложено модифицировать зацепление путём утонения витков червяка на торцевых участках, а также разработаны подходы к моделированию и улучшению параметров жидкостной смазки.
Несмотря на достигнутый прогресс, передачи с сопряжением «выпукло–вогнутый» – обеспечивающие повышенную нагрузочную способность, более плавный ход и высокую точность позиционирования – в отечественном машиностроении применяются ограниченно. Основными сдерживающими факторами являются технологическая сложность и высокая себестоимость изготовления. К ключевым причинам относятся низкая производительность операций формирования винтовой поверхности вогнутого профиля глобоидного червяка, а также значительная стоимость технологического оснащения (режущего инструмента и оборудования). Дополнительно остаётся нерешённой задача снижения трения в зацеплении и связанной с ним повышенной тепловой нагрузки глобоидной червячной передачи. Перспективным путём повышения эффективности приводов является модернизация процесса ротационного точения винтовой поверхности глобоидного червяка с вогнутым эвольвентным профилем посредством применения принудительно вращаемого многолезвийного инструмента. При этом зубья сопряжённого глобоидного цилиндрического колеса с выпуклым эвольвентным профилем целесообразно нарезать цилиндрической червячной фрезой, что позволяет отказаться от более дорогостоящей глобоидной червячной фрезы. Это даст возможность повысить производительность процесса и снизить стоимость производства.
Основная проблема существующих глобоидных червячных передач заключается в неэффективной конфигурации зацепления, которая снижает нагрузочную способность. Причиной является формирование контакта между рабочими поверхностями витков червяка и зубьев колеса при малых значениях приведённого радиуса кривизны и ограниченной общей протяжённости линий контакта. Такая геометрия зацепления связана с тем, что винтовая поверхность глобоидного червяка выполняется линейчатой при изготовлении. Требуется придать глобоидному червяку нелинейчатую форму винтовой поверхности для снижения контактного напряжения в зацеплении, повышения нагрузочной способности глобоидной червячной передачи, которая позволит уменьшить габариты и вес привода, а также повысит ресурс работы и КПД. К известным конструкциям относится передача ZT: червяк в ней имеет нелинейчатую винтовую поверхность с вогнутым профилем витков, а сопряжённое цилиндрическое колесо – зубья выпуклого профиля. Для передачи ZT характерно снижение контактных напряжений за счёт увеличения приведённого радиуса кривизны, а также более благоприятные условия формирования жидкостного трения. Вместе с тем технология изготовления таких передач сложна и затратна: требуется шлифование червяка тороидным кругом, что обуславливает низкую производительность и ограничивает промышленное распространение. В настоящее время наибольшее применение получили цилиндрические червячные передачи с линейчатой винтовой поверхностью витков червяка; они технологически просты, но уступают по показателям нагрузочной способности и КПД. Применение технологии ротационного точения позволяет получить ВП радиусного профиля с более высокой производительностью и низкой себестоимостью.
Разработанная методика расчета радиуса приведенной кривизны сопряженных рабочих поверхностей на основе моделирования геометрии глобоидного червяка и сопряженного с ним зубчатого колеса, а также экспериментальных исследований позволили определить кривизну профиля зуба и ВП глобоидного червяка, изготовленного ротационным точением. На основе кривизны профиля колеса и ВП глобоидного червяка рассчитывался радиус приведенной кривизны в зацеплении. График зависимости коэффициента снижения контактных напряжений Кδn от коэффициента Кс сопряжения радиусных рабочих поверхностей в зацеплении позволяет выбрать соответствующие параметры червячной пары.
На основе теоретических и экспериментальных исследований разработана методика образования зацепления профильно сопряженной глобоидно-цилиндрической пары. Методика может быть использована при проектировании и изготовлении профильно сопряженных глобоидных передач с заданной нагрузочной способностью. Расчеты показали, что коэффициент снижения контактного напряжения в зацеплении при проектировании опытной глобоидной пары составил Кδn = 2,56. При изготовлении глобоидно-цилиндрической профильно сопряженной червячной пары Кδn = 2,5, что подтверждает высокую сходимость полученных результатов на практике. Геометрические параметры ВП глобоидного червяка определили при помощи 3D-сканера Сreality CR-Scan Raptor.
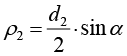
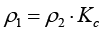
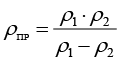
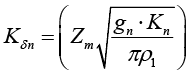