Введение
Основной задачей транспортной логистики является оптимизация маршрутов доставки, направленная на минимизацию затрат времени, топлива и других ресурсов. Одной из ключевых математических моделей для решения этой проблемы выступает задача коммивояжёра (TSP – Traveling Salesman Problem), заключающаяся в построении гамильтонова пути во взвешенном графе. TSP относится к классу NP-трудных задач, что делает применение точных методов неэффективным для графов большой размерности [1, с. 29-30]. На практике для решения задачи коммивояжёра широко применяются метаэвристические подходы, в особенности методы, основанные на принципах коллективного интеллекта и природных систем [2-4]. Среди наиболее эффективных мультиагентных методов следует выделить алгоритм муравьиной колонии (Ant Colony Optimization) и алгоритм роя частиц (Particle Swarm Optimization). Муравьиный алгоритм имитирует поведение насекомых при поиске оптимальных путей с помощью механизма феромонов [5-7]. Алгоритм роя частиц основан на координированном движении стайных организмов и их социальном поведении [8; 9]. Эти подходы демонстрируют высокую эффективность при поиске квазиоптимальных решений в сложных комбинаторных задачах, что обусловлено их способностью адаптироваться к изменяющимся условиям и находить баланс между исследованием пространства решений и эксплуатацией найденных хороших вариантов. В контексте задачи коммивояжёра оба алгоритма показывают устойчивые результаты, однако их сравнительная эффективность может существенно варьироваться в зависимости от специфики конкретного случая, что определяет актуальность их детального исследования и модификации для различных практических сценариев применения.
Следует отметить, что современные исследования включают и другие нечёткие метаэвристики для TSP, например: имитации отжига [10], гибридные алгоритмы [11], генетические алгоритмы [12]. Однако целенаправленное сравнение нечётких версий ACO и PSO, как наиболее репрезентативных алгоритмов роевого интеллекта с разной природой поиска, остаётся актуальной задачей. Это позволяет оценить эффективность нечёткого подхода к принципиально разным механизмам оптимизации.
Применение классических версий муравьиного алгоритма и метода роя частиц для решения TSP, несмотря на их эффективность, сталкивается с принципиальным ограничением – жёсткой детерминированностью модели. Традиционная постановка задачи предполагает точные, фиксированные значения весовых коэффициентов (временных, стоимостных или дистанционных), что противоречит вероятностной природе реальных транспортных систем. В действительности параметры перевозок часто носят неопределённый характер: стоимость может колебаться в зависимости от рыночных условий, а расстояния – корректироваться с учётом текущей внешней обстановки. Особенно ярко это проявляется в сложных климатических условиях, характерных для организации морской логистики в Арктической зоне, где расстояние между пунктами может существенно изменяться под влиянием динамической ледовой обстановки, сезонных факторов и изменчивых погодных условий, определяющих фактический путь судна [13; 14]. В связи с этим при моделировании транспортно-логистических систем необходимо учитывать широкий спектр ограничений [15, с. 81–89].
Для преодоления этого методологического разрыва предлагается модификация рассматриваемых алгоритмов путём введения элементов нечёткой логики. Такой подход позволит отразить неопределенность входных данных, адаптировать параметры алгоритмов к изменяющимся условиям, повысить устойчивость решений к вариациям входных параметров. В отличие от классических детерминированных версий, нечёткие модификации муравьиного алгоритма и метода роя частиц лучше соответствуют критерию практической адекватности, сохраняя операционную ценность решений при переносе в реальные условия транспортного планирования. Это достигается за счёт способности работать с «размытыми» входными данными и адаптивно корректировать поиск оптимальных маршрутов в условиях неполноты информации.
Целью данного исследования является разработка нечётких модификаций алгоритмов муравьиной колонии и роя частиц для решения задачи коммивояжёра в условиях неопределённости входных данных, с последующим сравнительным анализом их эффективности по критериям точности, скорости сходимости и устойчивости к вариациям параметров.
Материалы и методы решения
В классической задаче коммивояжёра рассматривается полносвязный ориентированный граф G = (V,E,W), где V = {1,2,…,n} представляет множество вершин (пунктов), E – множество дуг (маршрутов между пунктами), а W = (wij) – матрица весовых коэффициентов размерности n×n. Диагональные элементы матрицы wii = ∞ исключают остановку в текущей вершине. Требуется найти гамильтонов цикл минимальной длины, посещающий каждую вершину ровно один раз.
В исследовании для решения задачи коммивояжёра рассмотрим использование природных алгоритмов ACO и PSO.
Муравьиный алгоритм имитирует поведение муравьёв при поиске кратчайшего пути к источнику пищи. В основе алгоритма лежит механизм феромонных следов. Искусственные «муравьи» случайным образом исследуют граф, оставляя виртуальные феромоны на рёбрах, при этом вероятность выбора ребра зависит от концентрации феромонов и эвристической информации (например, обратной к длине ребра). Вероятность перехода из вершины i в вершину j имеет вид:
,
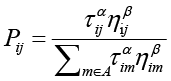где α, β – параметры, определяющие степень влияния, соответственно, феромонных следов и эвристической оценки при выборе следующей вершины; τij – феромонный след между вершинами i и j; ηij – эвристическая оценка, представляющая собой протяжённость пути между вершинами i и j; A – множество, содержащее все вершины, которые еще не посещены в текущем маршруте, обеспечивая построение допустимого решения.
Для адаптивного управления параметрами α и β муравьиного алгоритма предлагается использовать аппарат нечётких чисел. В рамках данного подхода параметры α (влияние феромона) и β (влияние эвристики) будут представлены как треугольные нечёткие числа: α = (αl, αc, αr), β = (βl, βc, βr), где левая граница отражает степень неопределенности в сторону минимальных значений параметра, центральное значение – наиболее вероятная оценка, правая граница отражает степень неопределенности в сторону максимальных значений параметра.
При использовании нечётких параметров вероятность перехода в следующую вершину графа в силу замкнутости операций [16] также будет нечётким числом Pij = (Pij l, Pij c, Pij r). Для преобразования нечёткого вывода в конкретное решение о следующей вершине маршрута применяется процедура дефазификации по методу центра тяжести:
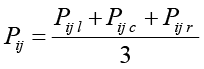
С течением времени более короткие пути накапливают больше феромонов, что усиливает их привлекательность для последующих агентов. Параллельно происходит испарение феромонов, предотвращающее застревание в локальных оптимумах. Изменение феромона на рёбрах графа на каждом шаге имеет вид:
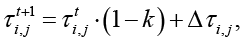
где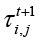 
– концентрация феромонного следа на следующем шаге; 
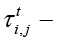концентрация феромонного следа на текущем шаге; k – параметр интенсивности испарения феромонного следа; 
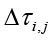– совокупный феромонный след, отложенный всеми агентами на ребре (i,j) в течение текущего шага алгоритма.
Алгоритм итеративно улучшает решение, сочетая принципы положительной обратной связи и стохастического поиска, что делает его эффективным для задач комбинаторной оптимизации, включая задачу коммивояжёра.
Метод роя частиц реализует принцип коллективного интеллекта, где каждая частица роя кодирует потенциальный маршрут в виде перестановки вершин графа. Начальная инициализация предполагает случайное распределение частиц в пространстве решений с присвоением им начальных координат xᵢ и векторов скорости vᵢ. Ключевыми параметрами алгоритма выступают когнитивный коэффициент c1, социальный коэффициент c2 и инерционный вес w. На каждом шаге обновляется вектор скорости vi:
,
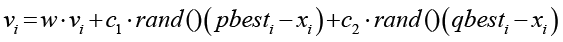где pbesti – лучшее индивидуальное решение, qbesti – лучшее коллективное решение, rand() – случайное число из [0,1].
Для корректировки положения частицы производится обновление её положения xᵢ = xᵢ + vᵢ. После обновления скорости и положения каждой частицы выполняется проверка и актуализация лучших найденных решений, что обеспечивает постоянное улучшение качества маршрутов в процессе оптимизации.
Для учёта неопределённости в условиях задачи коэффициенты c1 и c2 адаптируем через нечёткую логику. Представим указанные параметры алгоритма в виде нечётких треугольных чисел c1 = (c1l, c1a, c1r), c2 = (c2l, c2a, c2r). При переходе к нечёткому представлению параметров рассчитанные скорость и положение частицы приобретают аналогичную природу, формализуемую треугольными числами v = (vl, vc, vr), x = (xl, xc, xr). Метод сочетает быстроту сходимости за счёт социального взаимодействия частиц с гибкостью поиска, что делает его эффективным для решения задачи коммивояжёра.
Выбор треугольных нечётких чисел для представления параметров обусловлен простотой интерпретации, вычислительной эффективностью, адекватностью моделирования. Это позволяет сохранить баланс между точностью моделирования и производительностью алгоритма.
Результаты исследования и их обсуждение
Реализация нечётких алгоритмов производилась с использованием библиотеки работы с нечёткой логикой cikit-fuzzy языка программирования Python. Вычислительные эксперименты проводились на графе со 100 вершинами, со случайными координатами с равномерным распределением в единичном квадрате. Расстояния между вершинами вычислялись по евклидовой метрике с последующей линейной нормировкой всех весов рёбер к интервалу (0,1).
Результаты работы нечёткого муравьиного алгоритма с различными значениями параметров α (влияние феромона) и β (влияние эвристики) представлены в таблице 1. В верхней части каждой ячейки таблицы указана средняя длина маршрута, а в нижней – стандартное отклонение.
Как видно из таблицы 1, минимальная длина маршрута 7,88±0,52 достигнута при параметрах α=(1;1,2;1,4), β=(3,5;3,7;3,9). Наихудшие результаты наблюдались при β=(0;0,2;0,4), что объясняется недостаточным учетом эвристической информации в целевой функции вследствие доминирования феромонной составляющей в выборе пути и ранней сходимости к субоптимальным решениям.
Таблица 1
Длина маршрута (среднее ± ст. отклонение) при решении задачи коммивояжёра нечётким муравьиным алгоритмом
|
β α |
(0;0,2;0,4) |
(0,5;0,7;0,9) |
(1;1,2;1,4) |
(1,5;1,7;1,9) |
(2;2,2;2,4) |
(2,5;2,7;2,9) |
(3;3,2;3,4) |
(3,5;3,7;3,9) |
|
(0;0,2;0,4) |
41,70 ±2,85 |
32,37 ±2,11 |
21,09 ±1,45 |
15,42 ±1,01 |
12,10 ±0,79 |
11,09 ±0,65 |
10,24 ±0,58 |
9,71 ±0,55 |
|
(0,5;0,7;0,9) |
36,48 ±2,45 |
14,55 ±0,95 |
10,71 ±0,70 |
9,42 ±0,62 |
8,56 ±0,56 |
8,56 ±0,55 |
7,93 ±0,52 |
8,04 ±0,53 |
|
(1;1,2;1,4) |
17,41 ±1,15 |
10,65 ±0,70 |
8,78 ±0,58 |
8,14 ±0,54 |
8,58 ±0,56 |
8,50 ±0,56 |
8,38 ±0,55 |
7,88 ±0,52 |
|
(1,5;1,7;1,9) |
32,91 ±2,20 |
13,16 ±0,86 |
10,21 ±0,67 |
9,16 ±0,60 |
8,83 ±0,58 |
9,29 ±0,61 |
7,98 ±0,52 |
8,28 ±0,54 |
|
(2;2,2;2,4) |
34,84 ±2,30 |
15,94 ±1,04 |
11,88 ±0,78 |
10,14 ±0,66 |
10,21 ±0,67 |
9,44 ±0,62 |
8,20 ±0,54 |
8,35 ±0,55 |
|
(2,5;2,7;2,9) |
39,74 ±2,65 |
17,09 ±1,12 |
11,00 ±0,72 |
10,65 ±0,70 |
9,42 ±0,62 |
9,36 ±0,61 |
8,61 ±0,56 |
8,34 ±0,55 |
|
(3;3,2;3,4) |
39,67 ±2,64 |
18,58 ±1,21 |
13,85 ±0,91 |
11,28 ±0,74 |
10,58 ±0,69 |
9,14 ±0,60 |
8,91 ±0,58 |
8,53 ±0,56 |
|
(3,5;3,7;3,9) |
43,12 ±2,87 |
19,86 ±1,30 |
13,40 ±0,88 |
10,61 ±0,69 |
10,28 ±0,67 |
8,53 ±0,56 |
8,78 ±0,57 |
9,03 ±0,59 |
Примечание: составлено автором на основе полученных данных в ходе исследования.
Таблица 2
Длина маршрута (среднее ± ст. отклонение) при решении задачи коммивояжёра нечётким алгоритмом роя частиц
|
с1 с2 |
(0;0,1;0,2) |
(0,3;0,4;0,5) |
(0,6;0,7;0,8) |
(0,9;1;1,1) |
(1,2;1,3;1,4) |
|
(0;0,1;0,2) |
44,13±2,94 |
45,34±3,02 |
40,67±2,71 |
43,83±2,92 |
43,25±2,88 |
|
(0,3;0,4;0,5) |
43,41±2,89 |
45,55±3,04 |
42,56±2,89 |
46,95±3,13 |
43,69±2,91 |
|
(0,6;0,7;0,8) |
45,09±3,01 |
44,33±2,96 |
46,08±3,07 |
43,98±2,93 |
44,41±2,96 |
|
(0,9;1;1,1) |
43,75±2,92 |
43,37±2,89 |
44,28±2,95 |
41,73±2,78 |
44,80±2,99 |
|
(1,2;1,3;1,4) |
43,40±2,89 |
40,84±2,72 |
45,57±3,04 |
46,37±3,09 |
45,16±3,01 |
Примечание: составлено автором на основе полученных данных в ходе исследования.
Результаты работы нечёткого алгоритма роя частиц представлены в таблице 2. В верхней части каждой ячейки таблицы указана средняя длина маршрута, а в нижней – стандартное отклонение.
Согласно данным таблицы 2, оптимальная конфигурация параметров с1=(0,6;0,7;0,8), с2=(0;0,1;0,2) обеспечивает минимальную длину маршрута 40,67±2,71. Максимальное значение длины маршрута равно 46,95±3,13.
Исследования подтверждают преимущество нечёткого ACO перед нечётким PSO для задач средней размерности. Модифицированный муравьиный алгоритм показывает более стабильную и быструю сходимость, что подтверждает его эффективность для решения сложных задач транспортной логистики, в частности для оптимизации маршрутов в условиях Арктической зоны [17]. Это объясняется естественной интеграцией нечётких параметров (феромонного следа и видимости) в бионическую логику алгоритма, где «размытость» оценок создает гибкий механизм адаптации к интервальным данным и эффективно предотвращает застревание в локальных оптимумах. Учитывая результаты вычислений, полученных в работе [10], нечёткая версия алгоритма роя частиц демонстрирует рост вычислительной сложности. Это обусловлено необходимостью выполнения операций над нечёткими числами (сложение, умножение) и последующей дефазификации на каждой итерации для каждой частицы, что добавляет дополнительную вычислительную нагрузку по сравнению с классическим PSO, где все операции детерминированы и выполняются над скалярными значениями.
Заключение
Проведенное исследование демонстрирует, что нечёткие модификации алгоритмов оптимизации позволяют эффективно учитывать неопределённость входных данных при решении задачи коммивояжёра. Наибольшую эффективность показал муравьиный алгоритм, где введение нечётких параметров обеспечило баланс между адаптивностью и вычислительной сложностью. В отличие от этого, нечёткая версия алгоритма роя частиц, несмотря на теоретическую перспективность, продемонстрировала существенный рост вычислительных затрат без пропорционального улучшения качества решений, что ограничивает её практическое применение для рассматриваемого класса задач.
Особенно актуально это преимущество для задач морской логистики в Арктической зоне, где динамические изменения ледовой обстановки, погодных условий и сезонных маршрутов требуют гибкого подхода к планированию и высокой устойчивости к вариациям исходных данных.