Введение
Современные промышленные предприятия характеризуются высокой степенью автоматизации технологических процессов, в которых асинхронные электродвигатели составляют основу электромеханических систем [1]. Согласно статистическим данным, асинхронные двигатели потребляют до 45% всей производимой электроэнергии и обеспечивают функционирование критически важного оборудования [2; 3]. Внезапные отказы электроприводов приводят к значительным экономическим потерям, составляющим в среднем 50–100 тысяч рублей за час простоя производственной линии [4].
Анализ причин отказов асинхронных двигателей показывает, что 41,5% неисправностей связаны с подшипниковым узлом, 36,5% с обмотками статора, 9% – со стержнями ротора и 13% – с прочими причинами (рис. 1) [5; 6].
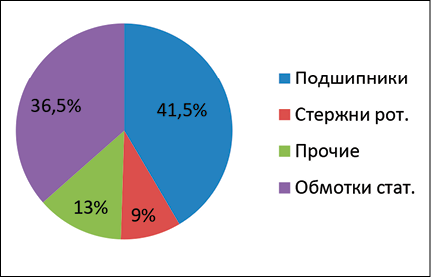
Рис. 1. Статистика распределения неисправностей электродвигателей
Такое распределение неисправностей обусловлено воздействием различных факторов: электрических перегрузок, механических напряжений, тепловых воздействий и загрязнений окружающей среды [7].
Существующие методы диагностики асинхронных двигателей можно разделить на две основные категории: методы параметрической идентификации, основанные на анализе электрических параметров двигателя, и методы машинного обучения, использующие статистические закономерности в диагностических признаках [8; 9]. Каждый подход имеет свои преимущества и ограничения, что требует проведения комплексного сравнительного анализа их эффективности.
Целью исследования является развитие методологии интеграции параметрических и обучаемых диагностических систем на основе анализа временных рядов сопротивления и индуктивности для выявления дефектов статорных обмоток асинхронных электродвигателей в нестационарных режимах.
Материалы и методы исследования
Теоретическую основу исследования составляют работы в области теории электрических машин, методов параметрической идентификации динамических систем и алгоритмов машинного обучения для задач классификации [10; 11]. Объектом диагностирования являлся трехфазный асинхронный электродвигатель типа АИР100S4У3 с короткозамкнутым ротором номинальной мощностью 3 кВт, номинальным напряжением 380 В, частотой вращения 1420 об./мин. и с обмоткой статора, выполненной по схеме «звезда».
Целью диагностирования является определение технического состояния двигателя ω ∈ Ω, где множество состояний Ω = {ω0 + ω1 + ω2} включает:
ω0 – номинальный режим работы (отсутствие повреждений);
ω1 – межвитковое замыкание в первой отпайке обмотки статора;
ω2 – межвитковое замыкание в третьей отпайке обмотки статора.
В составе гипотезы исследования рассматривались условия диагностирования в нестационарном режиме пуска электродвигателя при номинальном напряжении питания и отсутствии нагрузки на валу. Диагностические измерения фиксируются в интервале времени t ∈ T, где T = 1c – продолжительность переходного процесса пуска.
На основе наблюдаемых временных рядов токов статора
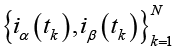
и напряжений
,
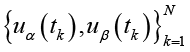измеренных с частотой дискретизации fs = 10 кГц (N = 10 000 отсчетов), требуется определить вектор диагностических признаков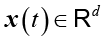 
и построить решающее правило D: ℝ→Ω, минимизирующее вероятность ошибочной классификации:
Perror = P{D(x) ≠ ωист}→min,
где ωист – истинное техническое состояние двигателя.
Исследование базировалось на математическом моделировании электромагнитных процессов в асинхронном двигателе и экспериментальном анализе диагностических алгоритмов. Математическая модель асинхронного двигателя в координатах α – β описывается системой дифференциальных уравнений Парка – Горева:
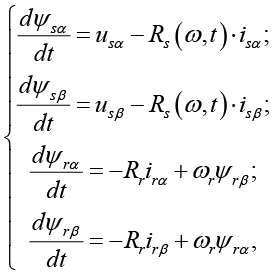
где ψsα, ψsβ – потокосцепления статора; ψrα, ψrβ – потокосцепления статора; Rs(ω,t), Rr – активные сопротивления обмоток статора и ротора; ωr – угловая скорость вращения ротора.
Для целей параметрической идентификации используется эквивалентная упрощенная модель, связывающая измеряемые величины напряжения и тока через параметры LM(t) и RM(t) – эквивалентные индуктивность и активное сопротивление обмотки статора [12]:
,
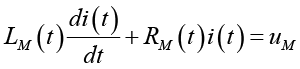где LM(t), RM(t) – настраиваемые параметры модели, изменяющиеся во времени при наличии повреждений; uM – выходное напряжение модели; i(t) – мгновенное значение тока двигателя.
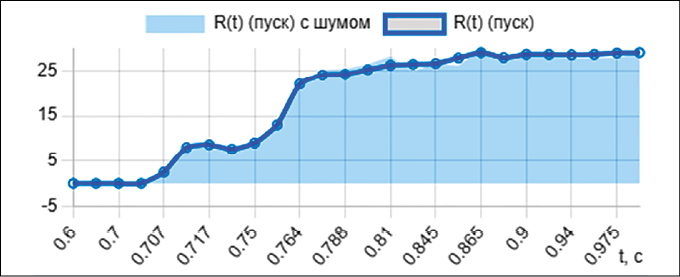
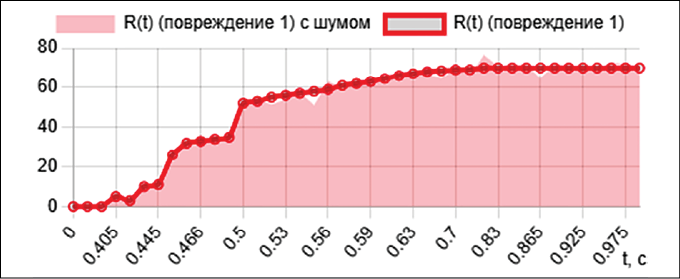
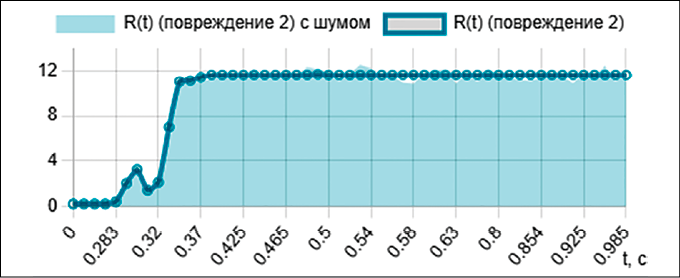
Рис. 2. Зависимости R(t) при пуске, повреждении первой отпайки (повреждение 1), повреждении третьей отпайки (повреждение 2) Примечание: составлено авторами на основе численных экспериментов
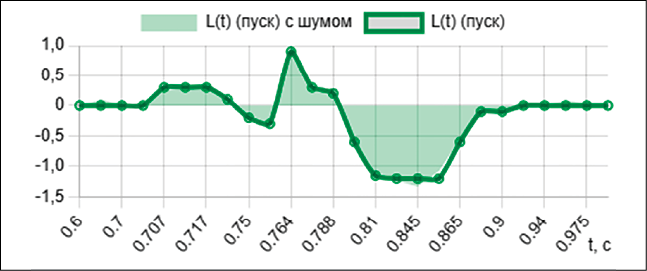
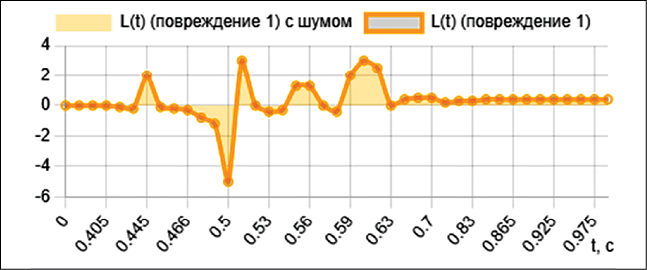
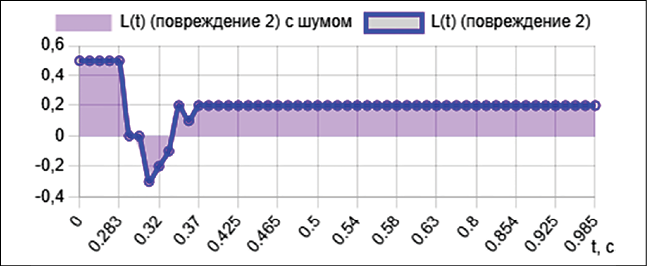
Рис. 3. Зависимости L(t) при пуске, повреждении первой отпайки (повреждение 1), повреждении третьей отпайки (повреждение 2) Примечание: составлено авторами на основе численных экспериментов
Данная модель справедлива для инженерного анализа переходных процессов и позволяет выявлять отклонения параметров LM(t) и RM(t) от номинальных значений при различных типах повреждений обмотки статора.
В результате численного решения системы уравнений методом Рунге – Кутты 4-го порядка получены зависимости эквивалентных активного сопротивления R(t) (рис. 2) и индуктивности L(t) (рис. 3) асинхронного электродвигателя для трех режимов его работы: пуск в номинальном режиме (ω0), повреждение первой отпайки обмотки статора (ω1) и повреждение третьей отпайки (ω2).
На основе полученных временных рядов RM(t) и LM(t) формируется вектор диагностических признаков:
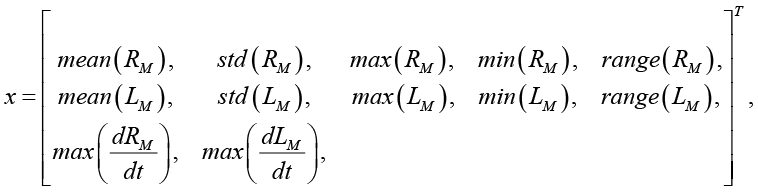
где mean(∙), std(∙), max(∙), min(∙), range(∙) – среднее значение, стандартное отклонение, максимум, минимум и размах соответствующего временного ряда.
Примененный алгоритм параметрической идентификации основан на методе наименьших квадратов для оценки параметров модели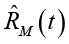 
, 
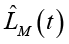[12] с минимизацией квадратичной функции ошибки:
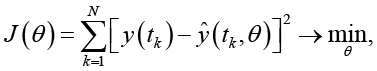
где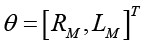 
– вектор идентифицируемых параметров; y(tk) – измеренное значение напряжения; 
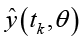– расчетное значение модели.
Для сравнения эффективности диагностики использовались методы машинного обучения: Random Forest (ансамбль из 200 деревьев решений), многослойная нейронная сеть с архитектурой 100-50-3 нейрона и метод опорных векторов с радиально-базисным ядром (RBF) [13; 14].
Экспериментальные исследования проводились в лаборатории электрических машин Вологодского государственного университета на стенде, включающем трехфазный асинхронный двигатель АИР100S4У3 (3 кВт, 380 В, 1420 об./мин.), систему питания на базе преобразователя частоты с возможностью программирования режимов пуска, датчики тока с диапазоном измерения ±50 А и точностью ±0,5%, 16-разрядный аналого-цифровой преобразователь и интерфейс передачи данных USB 2.0 с пропускной способностью 480 Мбит/с. Система сбора данных реализована на платформе MathLab и обеспечивает измерение мгновенных значений токов статора iα(t), iβ(t) с частотой дискретизации fs = 10 кГц и анализ временных рядов длительностью T = 1 с для каждого режима работы.
Программная реализация алгоритмов диагностики выполнена на кафедре информационных технологий Финансового университета при Правительстве Российской Федерации на языке программирования Python 3 с использованием библиотек NumPy, Pandas, Scikit-learn для численных расчетов и машинного обучения, Matplotlib для визуализации результатов. Веб-интерфейс для отображения диагностических данных разработан на основе HTML5, CSS3, JavaScript с библиотекой Chart.js [15, с. 83].
Результаты исследования и их обсуждение
Процесс обучения многослойной нейронной сети характеризовался динамикой функции потерь, которая определяется как среднеквадратичное отклонение между прогнозируемыми и фактическими значениями классификации по известной формуле:
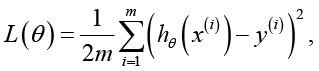
где θ – вектор весовых коэффициентов сети, m – размер обучающей выборки, hθ(x(i)) – выходное значение сети для i-го примера.
Экспериментальное исследование процесса обучения нейронной сети проводилось с использованием алгоритма оптимизации Adam с параметрами: скорость обучения α = 0,001, коэффициенты экспоненциального убывания β1 = 0,9, β2 = 0,999. Анализ кривой обучения показал характерное экспоненциальное убывание функции потерь (рис. 4).
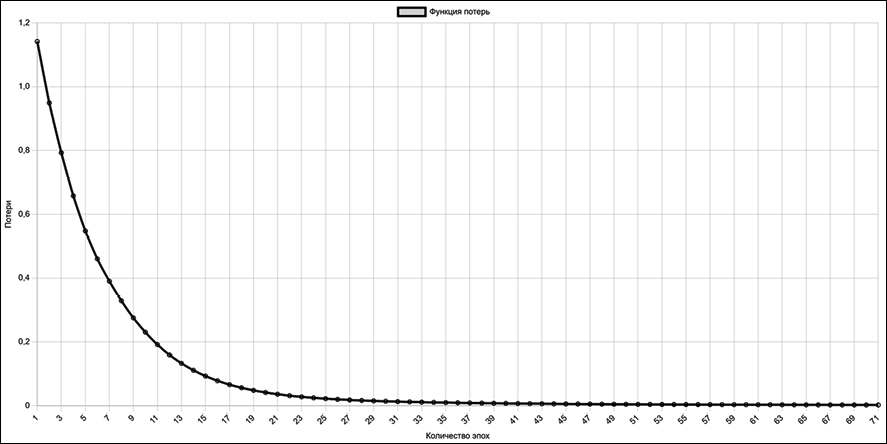
Рис. 4. График функции потерь нейронной сети в процессе обучения Примечание: составлено авторами на основе численных экспериментов
Начальное значение функции потерь составило 1,142, что свидетельствует о случайной инициализации весовых коэффициентов. В течение первых 20 эпох наблюдается интенсивное снижение потерь с 1,142 до 0.041, что соответствует логарифмической скорости убывания. Данная фаза характеризуется активной настройкой весовых коэффициентов скрытого слоя и формированием внутренних представлений диагностических признаков.
Последующие 30 эпох демонстрируют более медленную сходимость с асимптотическим приближением к значению 0,0022, достигнутому на 71-й эпохе обучения. Математическое моделирование процесса сходимости показало соответствие экспоненциальной зависимости вида:
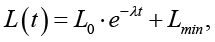
где L0 = 1,142 – начальное значение потерь, λ = 0,089 – коэффициент скорости сходимости, Lmin = 0,0022 – асимптотическое значение потерь, t – номер эпохи.
Коэффициент детерминации R2 = 0,987 подтверждает высокую степень соответствия экспериментальных данных теоретической модели сходимости.
Экспериментальное исследование алгоритма параметрической идентификации на основе метода наименьших квадратов продемонстрировало высокие показатели быстродействия при умеренной точности классификации. Временные характеристики алгоритма составили 0,51 ± 0,09 мс (доверительный интервал 95%), что свидетельствует о высокой стабильности вычислительных процессов. Точность классификации неисправностей достигла 85,2 ± 2,1%, при этом статистическая значимость результатов подтверждена критерием Стьюдента (p < 0,05).
Вычислительная сложность алгоритма характеризуется потреблением оперативной памяти объемом 12,3 КБ и выполнением 847 операций с плавающей точкой, что указывает на его применимость в системах с ограниченными ресурсами. Полученные результаты соответствуют теоретическим оценкам временной сложности O(n²) для решения системы линейных уравнений методом наименьших квадратов. Сравнительные характеристики методов диагностики асинхронных двигателей, включая время выполнения и точность идентификации параметров, представлены в таблице.
Промышленные условия эксплуатации характеризуются наличием электромагнитных помех и шумов измерительных систем, что требует оценки робастности диагностических алгоритмов. Экспериментальное исследование устойчивости проводилось с добавлением белого гауссова шума различной интенсивности к исходным сигналам токов статора.
Отношение сигнал/шум варьировалось в диапазоне от 40 до 10 дБ, что соответствует реальным промышленным условиям. Результаты показали, что параметрическая идентификация демонстрирует высокую устойчивость к шуму: при SNR = 20 дБ точность классификации снижается всего на 3,2% (с 85,2% до 82,0%).
Алгоритм Random Forest проявил наибольшую робастность среди методов машинного обучения, так как снижение точности при SNR = 20 дБ составило 4,8% (с 96,8% до 92,0%). Нейронные сети оказались наиболее чувствительными к шуму, при этом снижение точности достигло 8,1% (с 94,3% до 86,2%) при том же уровне помех.
Анализ алгоритмической сложности показал существенные различия между исследуемыми методами. Параметрическая идентификация имеет временную сложность O(n2), где n – размерность вектора параметров. Для типовой задачи диагностики n = 12 это обеспечивает стабильное время выполнения независимо от объема исторических данных.
Random Forest характеризуется сложностью обучения O(m∙logm∙d∙ntrees) и сложностью предсказания O(d∙ntrees), где m – размер обучающей выборки, d – количество признаков, ntrees = 200 – количество деревьев. При m = 4500 примеров и d = 12 признаков время обучения составляет 1,23 секунды.
Сравнительные характеристики методов диагностики асинхронных двигателей
|
Метод диагностики |
Время выполнения (мс) |
Точность (%) |
Сложность реализации |
Потребность в данных |
|
Параметрическая идентификация |
0,51 |
85,2 |
Низкая |
Низкая |
|
Random Forest |
7,23 |
96,8 |
Средняя |
Высокая |
|
Нейронные сети (MLP) |
12,5 |
94,3 |
Высокая |
Очень высокая |
|
SVM с RBF ядром |
8,8 |
92,1 |
Средняя |
Высокая |
Примечание: составлено авторами на основе экспериментальных данных.
Многослойная нейронная сеть имеет сложность обучения O(epochs∙m∙w), где w = 5653 – общее количество весовых коэффициентов. При 71 эпохе обучения общее время составило 45,6 секунды, что делает метод менее предпочтительным для частого переобучения модели.
Статистический анализ результатов показывает, что параметрическая идентификация обеспечивает преимущество в быстродействии в 18,7 раза по сравнению с алгоритмами машинного обучения, однако уступает в точности на 9,4%. Random Forest демонстрирует оптимальное соотношение точности и времени выполнения среди методов машинного обучения.
Заключение
Проведенное исследование позволило выполнить комплексный сравнительный анализ методов диагностики неисправностей асинхронных электродвигателей и разработать научно обоснованную методологию выбора оптимального подхода в зависимости от требований конкретного применения.
Установлено, что параметрическая идентификация обеспечивает существенное преимущество в быстродействии (0,51 мс против 9,5 мс в среднем для методов машинного обучения), что критично для систем реального времени. Однако алгоритмы машинного обучения демонстрируют значительно более высокую точность диагностики (94,6% против 85,2%), что важно для повышения надежности промышленных систем защиты.
Random Forest показал наилучшее соотношение точности и быстродействия среди алгоритмов машинного обучения, достигая точности 96,8% при времени выполнения 7,23 мс. Это делает его оптимальным выбором для большинства промышленных применений.