Введение
Мир трехмерной графики непрерывно эволюционирует, требуя от создателей контента не только художественного таланта, но и способности эффективно управлять все более сложными проектами. Традиционные подходы к 3D-моделированию, основанные на интуиции и кропотливом ручном труде, сохраняют свою непреходящую ценность, однако перед лицом возрастающих требований к детализации, скорости производства и гибкости внесения изменений возникает насущная потребность в оптимизации [1, с. 100]. 3D-графика является стремительно развивающимся направлением, которое внедряется в большое количество сфер жизни, начиная с рекламы и VFX-эффектов, а заканчивая игровой индустрией [2, с. 96]. При разработке 3D-моделей у художника всегда ограничен ресурс времени, и зачастую бывает, что одна задача накладывается на другую, что ведет к сдвигам общих сроков сдачи проекта, а это дополнительные финансовые расходы. Крайне важно уметь оптимизировать свою работу для увеличения продуктивности рабочего дня.
Цель исследования – разработка метода автоматизации моделирования с использованием математического подхода и скриптования 3D-объектов, а также исследование алгоритма оптимизации процесса 3D-моделирования.
Материал и методы исследования
Исследование проводилось в рамках игровой студии. Подготовительный этап: изучение литературы, выбор методов математического моделирования, формулирование гипотез. Основной этап: проведение экспериментов, создание и тестирование 3D-моделей с использованием выбранных методов. Анализ данных и написание статьи: обработка полученных результатов. Были выбраны следующие методы исследования: математическое моделирование, эксперимент и сравнительный анализ.
Результаты исследования и их обсуждение
Рассмотрим процесс создания 3D-модели параметрической винтовой лестницы. При традиционном подходе моделирования объекта в начале работы необходимо изучить референсы объекта из реальной жизни, можно сфотографировать существующее физическое строение, найти в поиске по картинкам или же обратиться к нейросетям (рис. 1) [3, с. 62].

Рис. 1. Референс винтовой лестницы Источник: составлено авторами на основе источника [4, с. 118]
После найденного подходящего под задачи референса необходимо рассчитать нужную высоту, радиус вращения, параметры ступеней, общий угол поворота лестницы [5, с. 230]. Далее создается черновой вариант модели, этот экземпляр имеет неточности и огрехи в передаче физического размера объекта (рис. 2). Также не стоит забывать про топологию: чем меньше граней, тем более оптимизирована модель и снижается ее итоговый объем, что в свою очередь благоприятно сказывается на работе всего проекта.

Рис. 2. Первичная модель винтовой лестницы Источник: составлено авторами на основе источника [6, с. 260]
Если посчитать затраченное время на создание такого рода модели, то можно получить следующие показатели:
1) поиск референса – в среднем 30 минут;
2) создание одной ступени – в среднем 60 минут;
3) расчет геометрических особенностей объекта – в среднем около 40 минут;
4) настройка и построение модели – в среднем 60 минут;
5) ретопология (упрощение) модели – в среднем 60 минут.
По первичным расчетам создание такого объекта при традиционном подходе моделирования составит свыше 4 часов, это очень затратно, учитывая, что это модель начального уровня [7, с. 138].
Необходимо разработать метод для более продуктивного подхода к работе 3D-художника. Именно здесь на передний план выходят методы математического моделирования, предлагая мощный инструментарий для формализации, автоматизации и повышения предсказуемости результатов. Интеграция математики в процесс создания трехмерных объектов открывает путь к параметрическому дизайну, процедурной генерации контента и прецизионной настройке геометрических характеристик, что находит широкое применение в разработке игр, промышленном дизайне, архитектурной визуализации и научных исследованиях [8, с. 358].
Рассмотрим применение математического моделирования для упрощения создания параметрической винтовой лестницы в Blender. На рынке 3D-пакетов программ есть огромное количество предложений, самые популярные из их Maya, Cinema 4D, 3D Max, Blender и др. Авторы использовали именно Blender, так как он имеет открытый исходный код и открыт для пользовательских модификаций, в то время как аналоги не имеют таких преимуществ. Будет использован Python-скриптинг (bpy), так как он позволяет наиболее прямолинейно работать с формулами со следующими параметрами:
− общая высота лестницы (H_total);
− радиус лестницы (до центральной оси ступеней) (R_staircase);
− количество ступеней (N_steps);
− общий угол поворота лестницы (в градусах) (Angle_total_degrees);
− глубина ступени (по радиусу) (Step_depth);
− ширина ступени (тангенциально) (Step_width);
− толщина ступени (Step_thickness).
Математическая модель представлена ниже:
1) высота одной ступени (h_step): каждая ступень поднимается на одинаковую высоту h_step = H_total / N_steps;
2) вертикальная позиция i-й ступени (z_i): положение i-й ступени по оси Z (где i от 0 до N_steps – 1). Будем считать, что z=0 – это основание первой ступени, z_i = i * h_step;
3) угловой шаг на одну ступень (angle_increment_rad): сначала переведем общий угол поворота из градусов в радианы [9, с. 155], так как тригонометрические функции в Python (и в математике) работают с радианами. Angle_total_rad = Angle_total_degrees * (π / 180). Затем разделим общий угол на количество ступеней, angle_increment_rad = Angle_total_rad / N_steps [10, с. 504].
4) угол поворота для i-й ступени (current_angle_rad_i): угол поворота i-й ступени вокруг вертикальной оси, current_angle_rad_i = i * angle_increment_rad;
5) горизонтальные координаты i-й ступени (x_i, y_i): это переход от полярных координат (радиус R_staircase, угол current_angle_rad_i) к декартовым:
− x_i = R_staircase * cos(current_angle_rad_i);
− y_i = R_staircase * sin(current_angle_rad_i);
6) ориентация ступени: каждая ступень должна быть повернута так, чтобы ее «передняя» часть была направлена тангенциально к спирали. Если авторы создают ступень так, что ее локальная ось X направлена вдоль ее глубины, а локальная ось Y – вдоль ширины, то нужно повернуть ступень вокруг ее локальной оси Z (которая совпадает с глобальной Z перед перемещением) на угол current_angle_rad_i [11, с. 123].
В начале задаются параметры лестницы (табл. 1), при вычислениях используются следующие параметры: общая высота лестницы, радиус лестницы, количество ступеней, общий угол поворота, глубина ступени, ширина ступени, толщина ступени [12, с. 95; 13, с. 35].
Таблица 1
Реализация скрипта для создания каркаса лестницы
|
# --- ПАРАМЕТРЫ ЛЕСТНИЦЫ --- H_total = 5.0 # Общая высота лестницы (в метрах) R_staircase = 1.5 # Радиус лестницы (до центра ступени) N_steps = 20 # Количество ступеней Angle_total_degrees = 360 # Общий угол поворота (например, 360 для полного круга) # Размеры ступени Step_depth = 0.8 # Глубина ступени (вдоль радиуса) Step_width = 0.3 # Ширина ступени (тангенциально) Step_thickness = 0.1 # Толщина ступени # --- ВЫЧИСЛЕНИЯ --- # 1. Высота одной ступени if N_steps == 0: print(«Ошибка: Количество ступеней не может быть равно нулю.») else: h_step = H_total / N_steps print(f”Высота одной ступени (h_step): {h_step:.3f} м”) # 3. Угловой шаг на одну ступень Angle_total_rad = math.radians(Angle_total_degrees) angle_increment_rad = Angle_total_rad / N_steps print(f”Угловой шаг на ступень (angle_increment_rad): {math.degrees(angle_increment_rad):.2f}° ({angle_increment_rad:.3f} рад)») |
Примечание: составлено авторами на основе полученных данных в ходе исследования.
Таблица 2
Реализация скрипта для создания ступеней
|
# --- СОЗДАНИЕ СТУПЕНЕЙ --- # Сначала создадим «прототип» ступени, который будем копировать # Создаем куб, который будет служить основой для ступени. # Его размеры будут (Step_depth, Step_width, Step_thickness) # Blender по умолчанию создает куб с центром в его геометрическом центре. # Авторы хотели, чтобы точка опоры ступени (ее «pivot point») была сзади по центру. # Поэтому создадим куб и затем сместим его в режиме редактирования # относительно его object origin. # Создание коллекции для ступеней (если еще не существует) stair_collection_name = “SpiralStaircase” if stair_collection_name not in bpy.data.collections: stair_collection = bpy.data.collections.new(stair_collection_name) bpy.context.scene.collection.children.link(stair_collection) else: stair_collection = bpy.data.collections[stair_collection_name] # Очистка предыдущих ступеней из коллекции (опционально) for obj in stair_collection.objects: bpy.data.objects.remove(obj, do_unlink=True) for i in range(N_steps): # 2. Вертикальная позиция i-й ступени z_i = i * h_step # Если хотим, чтобы центр ступени был на этой высоте, а не ее низ: # z_i = i * h_step + Step_thickness / 2.0 # Для простоты оставим z_i как низ ступени. # 4. Угол поворота для i-й ступени current_angle_rad_i = i * angle_increment_rad # 5. Горизонтальные координаты i-й ступени x_i = R_staircase * math.cos(current_angle_rad_i) y_i = R_staircase * math.sin(current_angle_rad_i) # Создаем меш для ступени (простой куб) # Размеры: X – глубина, Y – ширина, Z – толщина bpy.ops.mesh.primitive_cube_add( size=1, # Временный размер, изменим ниже enter_editmode=False, align=’WORLD’, location=(0, 0, 0) # Создаем в начале координат ) step_obj = bpy.context.active_object step_obj.name = f”Step_{i:03d}” # Устанавливаем правильные размеры ступени step_obj.dimensions = (Step_depth, Step_width, Step_thickness) bpy.ops.object.transform_apply(location=False, rotation=False, scale=True) # Применяем масштаб # Установка положения и вращения ступени # Положение (x_i, y_i, z_i) относится к центру ступени. # Смещаем на z_i + Step_thickness/2, чтобы низ ступени был на z_i step_obj.location = (x_i, y_i, z_i + Step_thickness / 2.0) # 6. Ориентация ступени # Поворачиваем ступень вокруг глобальной оси Z # Локальная ось X ступени будет направлена радиально от центра лестницы, # а локальная ось Y – тангенциально. # Если хотим, чтобы локальная ось X была тангенциальной (вдоль «ширины» ступени), # а Y – радиальной (вдоль «глубины»), то нужно повернуть еще на 90 градусов вокруг Z. # Допустим, стандартная ориентация куба: X – глубина, Y – ширина. step_obj.rotation_euler = (0, 0, current_angle_rad_i) # Перемещаем объект в коллекцию if step_obj.name in bpy.context.view_layer.objects: # если он в текущей сцене # убираем из основной коллекции сцены, если он там for coll in step_obj.users_collection: if coll == bpy.context.scene.collection: coll.objects.unlink(step_obj) # добавляем в коллекцию if step_obj.name not in stair_collection.objects: stair_collection.objects.link(step_obj) print(f”Создано {N_steps} ступеней в коллекции ‘{stair_collection_name}’.”) # Запуск скрипта: скопируйте этот код в текстовый редактор Blender и нажмите «Run Script». |
Примечание: составлено авторами на основе полученных данных в ходе исследования.

Рис. 3. Сгенерированная винтовая лестница Источник: составлено авторами по результатам данного исследования
Следом введенные данные используются для создания ступеней у лестницы (табл. 2). Учитывается положение объекта в пространстве, угол поворота, шаг поворота, расстояние от одной ступени до другой.
Сгенерированный 3D-объект гибок в изменениях, в пару кликов можно изменить любой параметр, и изменения сразу же отобразятся в программе (рис. 3) [14, с. 1495]. Проведем сравнение традиционного способа моделирования и моделирование с помощью скрипта (рис. 4) [15, с. 35].
Поиск референсов остался неизменным и составляет 30 минут, создание одной ступени сократилось в 4 раза, расчет геометрических особенностей сократился в 3 раза, настройка и построение сократились в 3 раза, а ретопология сократилась в 7,5 раз. При сравнении двух методов можно увидеть резкое сокращение времени у 4 из 5 пунктов, что говорит об успешности скриптового метода.
Проведем сравнительный анализ среди работников одного и того же квалификационного уровня. Рассмотрим двух 3D-художников, которые работают на уровне junior, у которых любительский уровень освоения программы. Опыт работы в трехмерной графике у них около 250 астрономических часов, что примерно составляет 2 года работы.
Перед ними была поставлена задача смоделировать винтовую лестницу по определенным параметрам традиционным методом. Вначале оба разработчика стали искать необходимые для работы референсы, что в среднем заняло около 25 минут.
Второй этап – это создание первой ступени лестницы. Первый разработчик начал свою работу с определения формы модели, размеров и пропорции, на эту задачу он потратил 70 минут. В то же время у второго работника на эти же действия было потрачено 55 минут работы.
Третий шаг – это расчет геометрических особенностей объекта. Первый специалист учёл особенности модели на предыдущем этапе, и этот этап у него занял 20 минут. В то же время у второго на этот этап было затрачено 40 минут работы из-за недостаточной проработки модели на прошлом этапе.
Настройка и построение модели, а также упрощение – у разработчиков заняло 100 и 115 минут соответственно.
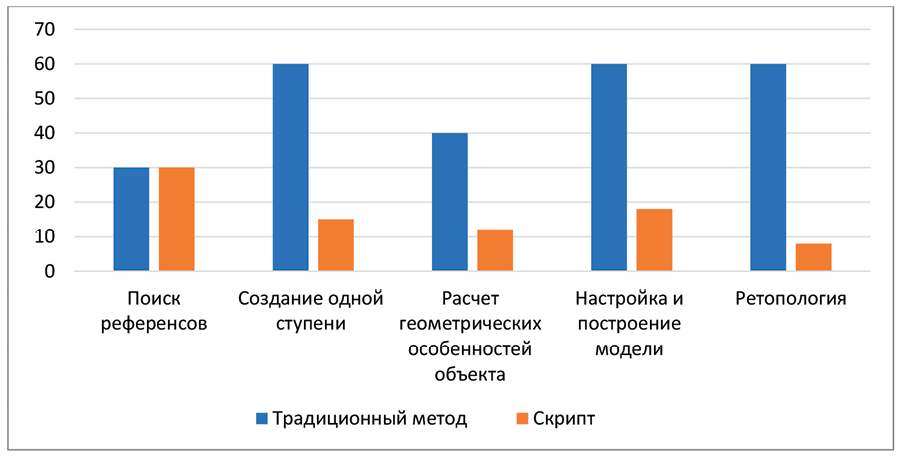
Рис. 4. Сравнительный анализ затраченного времени в минутах
Первый разработчик справился с заданием за 215 минут рабочего времени, в то время как второй решил поставленную задачу за 235 минут. Среднее время работы у разработчиков уровня junior составило 225 минут, а это 3 часа и 45 минут.
После использования традиционного метода работы испытуемым был предложен разработанный метод с использованием программного кода. Полный цикл у первого работника занял 90 минут, а у второго – 85 минут. Время работы при использовании скрипта сократилось на 66 процентов, что доказывает свою эффективность.
Заключение
Создание аддона (скрипт) – это инвестиция времени разработчика в то, чтобы сэкономить огромное количество времени множеству пользователей. Это хороший пример применения математического моделирования для оптимизации: математика не просто используется, а упаковывается в удобный инструмент, делая сложные процедурные техники доступными каждому художнику в Blender.
Результат эксперимента показал, что созданный скрипт уменьшил время работы над созданием и оптимизацией моделей. Математическое моделирование предоставляет мощные инструменты для оптимизации процессов, связанные с 3D-моделированием. Предложенный подход может быть использован для сокращения трудозатрат разработчиков 3D-моделей различных объектов. Дальнейшее развитие данного направления исследований может привести к еще более значительным улучшениям в области трехмерного моделирования.
Таким образом, математическое моделирование позволяет не только ускорить процесс создания 3D-моделей, но и повысить их качество. Используя расчеты для создания базовых форм, оптимизации сетки, художники могут значительно улучшить свои рабочие процессы и создавать более качественные модели.



