Введение
Практически все страны переживали такое явление, как демографический кризис, в разные периоды своей истории, и Российская Федерация, конечно же, не исключение. Последний кризис рождаемости в России происходил в 1991-2008 годах. Подобные явления специалисты связывают с демографическим переходом, то есть переход от традиционного общества (для которого характерна высокая рождаемость и высокая смертность) к индустриальному, а затем к постиндустриальному (для которых характерна низкая рождаемость и низкая смертность). На демографическую ситуацию влияют и уровень образованности населения, и качество жизни, и социально-экономическая ситуация. Для регулирования рождаемости в России вводятся демографические программы поддержки населения. Влияние этих программ на рождаемость может быть разнообразным и зависит от разных факторов, которые можно исследовать с помощью математического моделирования.
Целью исследования являлась разработка детерминированной теоретико-игровой многошаговой модели с конечным числом шагов исследования демографического процесса.
Материалы и методы исследования
Детерминированная теоретико-игровая многошаговая модель с конечным числом шагов строилась на основе методов и алгоритмов теории игр. В работе рассмотрены две поочередные многошаговые антагонистические игры, в которых участники процесса (игроки) на каждом шаге совершают свои выборы решений поочередно. В модели задействованы два участника, один из которых – регулирующий орган, он принимает решения в зависимости от складывающихся внешних и внутренних условий, влияющих на течение демографического процесса, с целью максимизация функции, зависящей от численности населения, вторым участником являются условия среды, цель которых противоположна целям регулирующего органа. Для исследования использовались статистические данные за 2021 год в России.
Результаты исследования и их обсуждение
Постановка задачи
Предполагаем, что руководящему органу требуется определить оптимальное чередование различных программ поддержки населения и многолетних программ в зависимости от ожидаемого характера условий среды каждого года планируемого цикла. Неопределенность долгосрочных прогнозов внешних условий обуславливает целесообразность теоретико-игрового подхода, если принять за агентов Ⅰ и Ⅱ, преследующих прямо противоположные цели, соответственно руководящий орган и условия среды. Тогда для конечного множества альтернатив, имеющихся в распоряжении руководящего органа, и конечного множества прогнозов условий среды на каждый год цикла можно построить позиционные игры, а затем найти оптимальную последовательность чередования [1; 2].
Допустим, что в первый год цикла планируется ввести программу поддержки населения № 1 на один год или многолетнюю программу А и что, согласно долгосрочному прогнозу, ожидается четыре варианта условий состояния среды, включающей в себя экономическое, политическое и социальное состояние среды (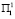 ,
, 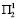 ,
, 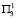 ,
, 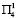 ). Если ввести программу № 1 и состояние среды первого года будут
). Если ввести программу № 1 и состояние среды первого года будут 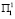 , то программа № 1 успеет положительно подействовать и на следующий год вводим программы № 2 и № 3. При этом программы № 1 и № 2 дают прирост населения для условий
, то программа № 1 успеет положительно подействовать и на следующий год вводим программы № 2 и № 3. При этом программы № 1 и № 2 дают прирост населения для условий 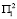 состояния среды второго года, равный t1, а для условий
состояния среды второго года, равный t1, а для условий 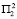 – равный t2. Программы № 1 и № 3 дают прирост, равный t3 и t4 соответственно для условий
– равный t2. Программы № 1 и № 3 дают прирост, равный t3 и t4 соответственно для условий 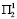 и
и 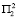 . Если же на первом году ввести программу поддержки № 1, а состояние среды окажется
. Если же на первом году ввести программу поддержки № 1, а состояние среды окажется 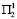 ,
, 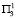 или
или 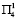 , то на второй год новые программы нельзя вводить, что обеспечивает прирост, равный соответственно t5, t6 и t7. Многолетняя программа А сменяется программой № 4 или № 5, если подтверждается прогноз условий среды
, то на второй год новые программы нельзя вводить, что обеспечивает прирост, равный соответственно t5, t6 и t7. Многолетняя программа А сменяется программой № 4 или № 5, если подтверждается прогноз условий среды 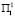 или
или 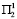 , и программой № 6 или № 7, если подтверждается прогноз условий
, и программой № 6 или № 7, если подтверждается прогноз условий 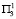 или
или 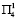 . При этом программа № 4 (№ 5) в условиях
. При этом программа № 4 (№ 5) в условиях 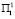 первого года дает прирост t8 или t9 (t10 или t11) в зависимости от условий
первого года дает прирост t8 или t9 (t10 или t11) в зависимости от условий 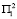 или
или 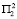 второго года, а в условиях
второго года, а в условиях 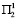 первого года дает прирост t12 (t13) независимо от условий второго года. Программы № 6 и № 7 в условиях
первого года дает прирост t12 (t13) независимо от условий второго года. Программы № 6 и № 7 в условиях 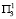 первого года, независимо от условий второго года, дают соответственно прирост t14 и t15, а в условиях
первого года, независимо от условий второго года, дают соответственно прирост t14 и t15, а в условиях 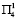 первого года – соответственно прирост t16 и t17.
первого года – соответственно прирост t16 и t17.
Решение поставленной задачи
Рассмотрим решение задачи, считая, что игрок Ⅱ не имеет информации о выбранных альтернативах агентом Ⅰ на каждом ходе. Очевидно, что первый ход делает агент Ⅰ, находясь в информационном множестве 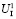 = {q1} и имея две альтернативы (1-я программа № 1, 2-я – многолетняя программа А). Второй ход принадлежит агенту Ⅱ, который находится в информационном множестве
= {q1} и имея две альтернативы (1-я программа № 1, 2-я – многолетняя программа А). Второй ход принадлежит агенту Ⅱ, который находится в информационном множестве 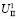 = {q2, q3}, и имеется четыре альтернативы (альтернатива k соответствует условиям среды первого года
= {q2, q3}, и имеется четыре альтернативы (альтернатива k соответствует условиям среды первого года 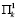 ). Третий ход делает агент Ⅰ, выбирая одну из двух альтернатив: в информационном множестве
). Третий ход делает агент Ⅰ, выбирая одну из двух альтернатив: в информационном множестве 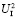 = {q4} альтернатива 1 – программа № 2 и альтернатива 2 – программа № 3; в информационном множестве
= {q4} альтернатива 1 – программа № 2 и альтернатива 2 – программа № 3; в информационном множестве 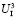 = {q5, q6} альтернатива 1 – программа № 4 и альтернатива 2 – программа № 5; в информационном множестве
= {q5, q6} альтернатива 1 – программа № 4 и альтернатива 2 – программа № 5; в информационном множестве 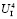 = {q7, q8} альтернатива 1 – программа № 6 и альтернатива 2 – программа № 7. Четвертый ход делает агент Ⅱ, находясь в информационном множестве
= {q7, q8} альтернатива 1 – программа № 6 и альтернатива 2 – программа № 7. Четвертый ход делает агент Ⅱ, находясь в информационном множестве 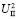 = {q9, q10, q11, q12} и выбирая одну из двух альтернатив (альтернатива 1 – условия среды второго года
= {q9, q10, q11, q12} и выбирая одну из двух альтернатив (альтернатива 1 – условия среды второго года 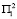 , альтернатива 2 – условия среды второго года
, альтернатива 2 – условия среды второго года 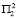 ). Стратегии агента Ⅰ можно записать как следующую систему ||i1||i2||, где i1 – альтернатива, выбираемая на первом ходе (i1 = 1, 2), а i2 – альтернатива, выбираемая на третьем ходе (i2 = 1, 2). Стратегии агента Ⅱ можно записать как следующую систему ||j1||j2||, где j1 – альтернатива, выбираемая на втором ходе (j1 = 1, 2, 3, 4), а j2 – альтернатива, выбираемая на четвертом ходе (j2 = 1, 2) [3-4]. В результате функция выигрыша агента Ⅰ будет представлена таблицей 1.
). Стратегии агента Ⅰ можно записать как следующую систему ||i1||i2||, где i1 – альтернатива, выбираемая на первом ходе (i1 = 1, 2), а i2 – альтернатива, выбираемая на третьем ходе (i2 = 1, 2). Стратегии агента Ⅱ можно записать как следующую систему ||j1||j2||, где j1 – альтернатива, выбираемая на втором ходе (j1 = 1, 2, 3, 4), а j2 – альтернатива, выбираемая на четвертом ходе (j2 = 1, 2) [3-4]. В результате функция выигрыша агента Ⅰ будет представлена таблицей 1.
Таблица 1
Функция выигрыша игрока Ⅰ
|
Стратегия игрока I |
||||||||
|
||1||1|| |
||1||2|| |
||2||1|| |
||2||2|| |
||3||1|| |
||3||2|| |
||4||1|| |
||4||2|| |
|
|
||1||1|| |
t1 |
t2 |
t5 |
t5 |
t6 |
t6 |
t7 |
t7 |
|
||1||2|| |
t3 |
t4 |
t5 |
t5 |
t6 |
t6 |
t7 |
t7 |
|
||2||1|| |
t8 |
t9 |
t12 |
t12 |
t14 |
t14 |
t16 |
t16 |
|
||2||2|| |
t10 |
t11 |
t13 |
t13 |
t15 |
t15 |
t17 |
t17 |
Пусть tk принимает такие значения, что функцией выигрыша агента Ⅰ будет матрица
 .
.
Лемма. Пусть Г = <x, y, H> – конечная антагонистическая игра, Г’ = <x\x0, y, H> – подыгра игры Г, а x0 – чистая стратегия игрока Ⅰ в игре Г, доминируемая некоторой стратегией X0, спектр которой не содержит x0. Тогда всякое решение (X*, Y*, v) игры Г’ является решением игры Г [5, с. 20]. Следовательно, всякое решение игры Г1 является решением игры Г.
Представим игру Г1 (руководящий орган выбирает 1-ю альтернативу на 1-м ходе) матрицей
 .
.
Из анализа матрицы H1 понятно, что при подтверждении прогноза условий среды 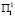 в первый год и
в первый год и 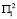 на второй год, либо
на второй год, либо 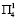 в первый год прирост рождаемости будет составлять 27.3∙104 человек, либо 24.2∙104, что составит максимальный прирост. Если же условия среды будут
в первый год прирост рождаемости будет составлять 27.3∙104 человек, либо 24.2∙104, что составит максимальный прирост. Если же условия среды будут 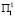 и
и 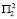 , соответственно в первый и во второй год, то прирост рождаемости составит 29∙104 человек. При условиях
, соответственно в первый и во второй год, то прирост рождаемости составит 29∙104 человек. При условиях 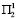 и
и 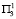 прирост 49∙104 новорожденных и 50∙104 новорожденных соответственно. Далее рассмотрим ситуацию выбора 2-й альтернативы на первом ходе. По лемме решение игры Г2 может быть решением игры Г. Представим игру Г2 матрицей
прирост 49∙104 новорожденных и 50∙104 новорожденных соответственно. Далее рассмотрим ситуацию выбора 2-й альтернативы на первом ходе. По лемме решение игры Г2 может быть решением игры Г. Представим игру Г2 матрицей
 .
.
Сопоставляя матрицу H2, получаем следующие результаты. При условиях 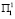 и
и 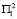 , соответственно в первый и во второй год, либо при
, соответственно в первый и во второй год, либо при 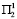 ожидается прирост рождаемости, равный 51.7∙104 человек. Если подтверждается условие
ожидается прирост рождаемости, равный 51.7∙104 человек. Если подтверждается условие 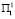 в первый год и
в первый год и 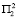 во второй год, либо
во второй год, либо 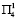 , то прирост рождаемости составит 57.7∙104 человек. При условиях
, то прирост рождаемости составит 57.7∙104 человек. При условиях 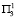 прирост равен 44.7∙104 новорожденных, что составит максимальный прирост.
прирост равен 44.7∙104 новорожденных, что составит максимальный прирост.
Таким образом, агент Ⅰ выбирает альтернативу 1 на первом ходе и альтернативу 2 на третьем ходе, либо альтернативу 2 на первом ходе и альтернативу 1 на третьем ходе, если на втором ходе будет выбрана альтернатива 1 или 2, и альтернатива 2, если на втором ходе будет выбрана альтернатива 3 или 4. В содержательной терминологии задачи необходимо ввести программу поддержки населения № 1 в первый год и программу № 3 во второй год либо ввести многолетнюю программу А в первый год и программу № 4 во второй год, если подтвердится прогноз 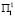 или
или 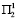 , и программу № 7 – во второй год, если подтвердится прогноз
, и программу № 7 – во второй год, если подтвердится прогноз 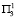 или
или  .
.
Вероятные выигрыши в условиях переменной удельной стоимости
Рассмотрим наиболее вероятные выигрыши из первой части задачи в условиях переменной удельной стоимости, выделяемой на поддержку одной семьи [6-8]. Пусть руководящий орган имеет в своем распоряжении L женщин, находящихся в репродуктивном возрасте, и может ввести m программ поддержки населения. Обозначив через yi прирост рождаемости после введения программы типа i, через ξi – долю населения, на которую направлена i-я программа, а через pi – удельную стоимость, необходимую для поддержки семьи после рождения ребенка, можно выразить общую стоимость формулой
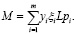 (1)
(1)
Удельная стоимость является функцией от количества новорожденных, родители которых воспользовались i-й программой поддержки населения демографии, то есть
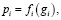 (2)
(2)
где gi – общее количество новорожденных после ввода в действие программы i-го типа.
Можно считать, что
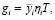 (3)
(3)
где 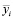 – средний прирост рождаемости после программы i-го типа, T – общая численность женского населения, находящегося в репродуктивном возрасте, а ηi – доля численности населения, на которое направлена программа типа I [9]. Подставляя формулы (2) и (3) в (1),
– средний прирост рождаемости после программы i-го типа, T – общая численность женского населения, находящегося в репродуктивном возрасте, а ηi – доля численности населения, на которое направлена программа типа I [9]. Подставляя формулы (2) и (3) в (1),
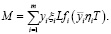 (4)
(4)
Обозначив через агента Ⅰ – руководящий орган, а через агента Ⅱ – условия среды, приходим к антагонистической игре, в которой стратегиями агента Ⅰ будут векторы
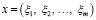 ,
, 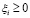 ,
, 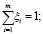
стратегиями агента Ⅱ – векторы
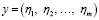 ,
, 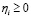 ,
, 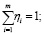
функция выигрыша задается формулой (4). Очевидно, что чем в большей мере население воспользуется одной из программ, тем меньше удельная стоимость затрат на каждую семью. Следовательно, каждая из функций fi монотонно убывает [9]. Будем считать, что это убывание происходит с показательной скоростью, то есть каждая из функций fi имеет вид 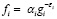 ; для которой коэффициенты αi и показатели εi вычисляются статистическими методами [10, с. 146].
; для которой коэффициенты αi и показатели εi вычисляются статистическими методами [10, с. 146].
После подстановки выражения для fi в формулу (4) получим
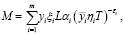
или 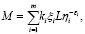 (5)
(5)
где 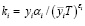 . В этом случае функция выигрыша (5) является линейной по стратегии агента Ⅰ и выпуклой относительно стратегии агента Ⅱ [9]. Следовательно, на основании теорем 1 и 2, каждый из игроков имеет оптимальные чистые стратегии [5, с. 34].
. В этом случае функция выигрыша (5) является линейной по стратегии агента Ⅰ и выпуклой относительно стратегии агента Ⅱ [9]. Следовательно, на основании теорем 1 и 2, каждый из игроков имеет оптимальные чистые стратегии [5, с. 34].
Теорема 1. Если x и y – сепарабельные компакты, множество x выпукло, а функция H непрерывна на x×y и вогнута по x при каждом значении y, то в игре Г = <x, y, H> первый игрок имеет оптимальную чистую стратегию.
Таблица 2
Оптимальные стратегии
|
Вид стратегии |
№ 1 и № 3 |
А и № 4 |
|
Показатели |
1 |
2 |
|
εi αi |
27,3 1,85 (1,52∙109)1,85 = 9,69∙1016 |
51,7 2,63 (3,56∙109)2,63 = 2,05∙1025 |
|
ki |
3,030 |
4,000 |
|
Вид стратегии |
А и № 7 |
№ 1 |
|
Показатели |
3 |
4 |
|
εi αi |
44,7 5,00 (1,20∙109)5 = 2,49∙1045 |
24,2 0,515 (1,47∙109)0,515 = 5,27∙104 |
|
ki |
0,003 |
13,750 |
Примечание: составлено авторами на основе источников: Демографический прогноз населения до 2035 [Электронный ресурс] / Росстат. URL: https://rosstat.gov.ru/folder/12781 (дата обращения: 02.05.2025); Численность постоянного населения на 1 января [Электронный ресурс] / Росстат. URL: https://showdata.gks.ru/report/278928/ (дата обращения: 06.05.2025).
Теорема 2. Если x и y – сепарабельные компакты, множество y выпукло, а функция H непрерывна на x×y и выпукла по y при каждом значении x, то в игре Г = <x, y, H> второй игрок имеет чистую оптимальную стратегию.
Найдем оптимальные стратегии агента Ⅰ (руководящий орган) и агента Ⅱ (внешних и внутренних условий), используя данные из первой части работы по ведению таких стратегий, как ||1||1||, ||1||2||, ||2||1|| и ||2||2|| со стороны руководящего органа и стратегии ||1||1||, ||2||1||, ||3||1|| и ||4||1|| со стороны внешних условий [11]. Иными словами, будем исследовать оптимальность введения программ № 1 и № 3, только № 1, многолетнюю программу А и № 4 или многолетнюю программу А и № 7. Таким образом, T = 7 500 000, а остальные данные приведем в таблице 2.
После подстановки величин T, yi, yi εi, αi в формулу (5) получим [12]
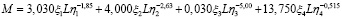 .
.
Тогда
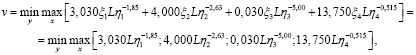
а минимум правой части последнего равенства достигается при соотношении
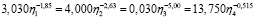 .
.
Отсюда получим систему уравнений [13]
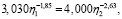
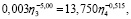
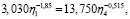
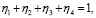
решением которой является вектор y*= (0,262; 0,432; 0,153; 0,153), а v = 36,1∙104 – прирост рождаемости с одной программы [14].
Для вычисления оптимальных стратегий агента Ⅰ найдем частные производные функции 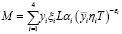 по аргументам ηi (i = 1,2,3) [15].
по аргументам ηi (i = 1,2,3) [15].
Учитывая, что 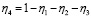 и
и 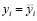 , а затем приравнивая их к нулю, получим
, а затем приравнивая их к нулю, получим
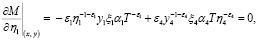
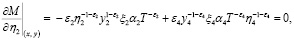
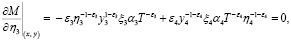
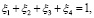
решением будет вектор x*= (0,246; 0,184; 0,053; 0,517).
Таким образом, оптимальная стратегия руководящего органа состоит в выделении под i-ю программу долю ξi населения численности L, а значение игры (ожидаемый доход в наименее благоприятном случае) – прирост с одной программы v = 36,1∙104 новорожденных. При этом наименее благоприятный случай возникает тогда, когда реализуются условия среды согласно y*, что возникает вследствие монотонного убывания каждой из функций fi.
Заключение
В результате были рассмотрены две задачи:
1) при выборе на первом ходе 1-й альтернативы прирост составит 24.2∙104 новорожденных, а 2-й – 44.7∙104 новорожденных;
2) под i-ю программу выделить долю ξi населения численности L, а значение игры (ожидаемый доход в наименее благоприятном случае) равно v = 36,1∙104 новорожденных. Востребованность программы влечет за собой уменьшение удельной стоимости затрат на каждую семью в рамках данной программы.




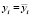 (10 тыс.)
(10 тыс.)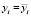 (10 тыс.)
(10 тыс.)