Под безопасностью понимают состояние защищенности человека или инженерно-технической и программной инфраструктуры в различных условиях от возможных опасностей и их сочетания путем установления в отношении системы заданных параметров функционирования, а также минимизации опасностей, исходящих от человека и самой системы.
Составляющие безопасности включают в себя различные виды мероприятий и действий, направленных на обеспечение безопасности. Они могут быть предотвращающими, реактивными или непосредственными действиями, а также могут включать использование различных технологий и методов.
Одной из главных составляющих безопасности является физическая безопасность, которая относится к мерам, направленным на предотвращение угроз физических повреждений людей и ущерба материальным ценностям. Это может включать использование видеонаблюдения, охранной сигнализации, контроля доступа и даже физической охраны.
Еще одной составляющей безопасности является информационная безопасность, которая связана с защитой конфиденциальной, ценной информации от несанкционированного доступа, использования или распространения [1, с. 48]. Для обеспечения информационной безопасности могут применяться меры, такие как шифрование данных, использование паролей и биометрических идентификаторов, межсетевые экраны и антивирусное программное обеспечение [1, с. 61]. Злоумышленники в своей деструктивной деятельности руководствуются собственными целями, как правило, ориентированными на дестабилизацию информационного поля и нанесение репутационных потерь.
Кроме того, безопасность может быть связана с обеспечением безопасности рабочего места или даже с противопожарной безопасностью, которая включает в себя соблюдение требований пожарной безопасности и наличие необходимых систем пожаротушения.
В целом в исследованиях значительное внимание уделяется вопросам информационной безопасности. Так в [2] уделено внимание разработке математического подхода для обеспечения безопасности коалиций микросетей в условиях кибератак. В [3] кооперативное взаимодействие рассматривается как механизм определения дележа денежных сумм. То есть присутствует экономический контекст. В [4] дается анализ и формализация взаимодействия, но без практического применения именно теории кооперативных игр. Также существуют исследования, например [5, 6], в которых рассматриваются направления развития вектора Шепли, но не принципиально меняющие его функционал.
Данное исследование отличается от существующих анализом практических аспектов применения вектора Шепли к оценке безопасности «не информационных систем». Результаты исследования могут быть применены к системам технического и организационного характера. Кроме того, в публикации анализируются различные варианты приложения вектора Шепли.
Целью данной работы является исследование возможности применения теории кооперативных игр и вектора Шепли для нахождения коалиции (сочетания) мероприятия по обеспечению безопасности для максимизации эффективности противодействия деструктивной деятельности, а также исследование применение вектора для оценки степени влияния этой деятельность на безопасность системы.
Материалы и методы исследования
Введем понятие «деструктивная деятельность» (ДД) – планируемое и (или) практически реализуемое воздействие на уровень безопасности системы (охраняемого объекта) с целью понижения этого уровня и (или) создания условий для такого понижения.
Для обеспечения безопасности на охраняемых объектах и в системах применяется ряд мероприятий, которые направлены на предотвращение, пресечение или недопущение ДД от любых источников.
Мероприятие по обеспечению безопасности (МпОБ) – мероприятие, направленное на выявление и предотвращение действий и их последствий, направленных на понижение режима безопасности и связанных в том числе с причинением вреда жизни и здоровью людей, а также нанесением различных видов ущерба на охраняемом объекте (территории).
Сочетание различных мероприятий по обеспечению безопасности позволяет создать комплексную систему защиты, которая обеспечит надежную защиту объекта и его сотрудников от возможных угроз и рисков. Однако важно отметить, что эффективность такой системы будет зависеть от правильного выбора и применения мер, а также от оценки и учета специфики конкретного объекта и его потенциальных уязвимостей.
Степень негативного влияния ДД зависит от МпОБ. Чем меньше эффективность мероприятия, тем выше вероятность того, что любое (даже самое простое) действие будет деструктивным и, наоборот, чем мероприятия эффективнее, тем меньше вероятность, что самая сложная ДД понизит режим безопасности. Обеспечение безопасности является важной задачей, требующей комплексного подхода. ДД злоумышленников представляет серьезную угрозу, однако с помощью соответствующих мероприятий эта угроза может быть полностью нейтрализована или сведена к минимуму.
В данной работе предлагается для определения сочетания МпОБ для нейтрализации ДД и оценки эффективности МпОБ применить вектор Шепли [7, с. 157].
Вектор Шепли – это концепция, разработанная математиком Шепли, которая находит свое применение в игровой теории. В этом поле исследования вектор Шепли играет важную роль в определении справедливого распределения выигрышей в коалиционных играх, где группы игроков объединяются в коалиции для достижения общей цели.
Основная идея метода Шепли заключается в определении вклада каждого игрока в формирование выигрышной коалиции. Для этого учитывается, как бы изменилась ситуация, если бы данный игрок присоединился или покинул текущую коалицию. Таким образом, метод Шепли оценивает значимость каждого игрока и определяет, сколько ему следует получить от общей выгоды.
Вектор Шепли удовлетворяет следующим свойствам [8]. Свойство эффективности показывает, что весь выигрыш большой коалиции должен быть распределен между игроками. Сумма выигрышей игроков равна выигрышу большой коалиции. Свойство симметричности – игроки, которые вносят одинаковый вклад, должны получить одинаковые выигрыши. Болваном в теории кооперативных игр называется бесполезный игрок, не вносящий вклада ни в какую коалицию. Линейность – выигрыш игрока в сумме игр должен равняться сумме его выигрышей в каждой из игр.
В связи с тем, что понятие безопасности является комплексным (ДД и МпОБ формируют систему), для оценки уровня безопасности нужно выполнить формализацию ДД и МпОБ .
При условии, что для нейтрализации ДД могут применяться различные МпОБ, введем обозначение
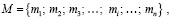(1)
где mi – i-е МпОБ;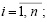 
n – количество МпОБ.
С учетом того, что каждое мероприятие представляет собой комплекс практических действий по обеспечению безопасности, каждое мероприятие можно представить как
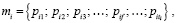(2)
где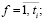 
ti – количество практических действий для i-го МпОБ.
С учетом того, что для понижения уровня безопасности системы может быть реализовано множество ДД, введем обозначение
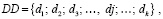(3)
где dj – j-е ДД;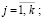 
k – количество деструктивных воздействий.
Таким образом, необходимо найти такое сочетание МпОБ из M, при котором для каждого ДД из DD обеспечивалась бы максимальная эффективность нейтрализации ДД. В связи с тем, что вектор Шепли является важным инструментом в теории кооперативных игр и может быть использован для анализа и оценки различных сценариев кооперации, предлагается рассмотреть возможность его применения для решения задачи оценки соответствия и степени нейтрализации ДД с учетом имеющегося множества МпОБ:
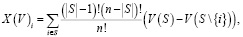(4)
где i= 1,2…n; X – дележ; S – количество игроков; n – количество участников дележа, V – оценка эффективности МпОБ.
Оценку V предлагается осуществлять на основе анализа эффективности действий, составляющих МпОБ. Экспертный вариант оценивания обосновывается тем, что МпОБ носят комплексный характер, и их формализация и аналитическое вычисление V могут быть затруднены.
Результаты исследования и их обсуждение
Рассмотрим возможность достижения поставленной задачи на примере. Предположим, что есть некоторая ДД, которая может негативно отразиться на уровне безопасности системы и есть три МпОБ, способные частично или полностью нейтрализовать ДД
М = {m1; m2; m3}. (5)
Причем каждое из МпОБ состоит из определенных практических действий, эффективность которых по отношению к некоторой ДД может быть экспертно оценена, например, в диапазоне от 0 до 100. При этом шкала может быть любой, но одинаковой для всех действий. Применительно к МпОБ предлагается трактовать оценку как степень эффективности мероприятия для обеспечения безопасности системы (табл. 1).
Таблица 1
Экспертная оценка эффективности практических действий по отношению к ДД
|
Практическое действие |
p1 |
p2 |
p3 |
p4 |
p5 |
|
Экспертная оценка |
10 |
15 |
15 |
25 |
10 |
Следует отметить, что ни одно отдельное практическое действие не обладает высокой эффективностью против ДД, а также суммарная эффективность всех действий менее 100. Следовательно, необходимо определить сочетание МпОБ.
Тогда для множества МпОБ (5) получим оценки эффективности, представленные в табл. 2. В данном случае эффективность определена простым арифметическим суммированием. Однако могут быть применены и другие способы ее вычисления. Требование единообразия для всех МпОБ обязательно.
Как видно из таблицы, МпОБ формируются на основе одинаковых практических действий. Например, m1 и m2 включают действия p1 и p5. В реальных условиях может возникать вопрос целесообразности реализации повторяющихся действий. Кроме того, может быть рассмотрен случай, когда реализация некоторых действий может приводить к синергетическому эффекту из-за чего суммарная эффективность может быть выше.
Таблица 2
Оценка эффективности МпОБ по отношению к ДД
|
p1 |
p2 |
p3 |
p4 |
p5 |
Оценка эффективности МпОБ, V |
|
|
m1 |
10 |
0 |
0 |
25 |
10 |
45 |
|
m2 |
10 |
0 |
15 |
0 |
10 |
35 |
|
m3 |
10 |
15 |
0 |
25 |
10 |
60 |
В соответствии с базовыми положениями теории кооперативных игр на основе МпОБ могут быть сформированы коалиции
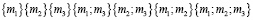. (6)
Для каждой коалиции МпОБ значение характеристической функции V вектора Шепли также определим простым арифметическим суммированием. Результаты представлены в табл. 3. Однако, как и для оценки эффективности МпОБ могут быть применены и другие способы вычисления V. Требование единообразия вычислений также обязательно. Кроме того, может быть рассмотрен случай синергетического эффекта для определенных сочетаний МпОБ, тогда совместная реализация определенных МпОБ может давать дополнительную эффективность.
Таблица 3
Характеристическая функция вектора Шепли для коалиций
|
V({m1}) |
V({m2}) |
V({m3}) |
V({m1; m2}) |
V({m2; m3}) |
V({m1; m3}) |
V({m1; m2; m3}) |
|
|
Повторяемость действий |
45 |
35 |
60 |
80 |
95 |
105 |
140 |
|
Неповторяемость действий |
45 |
35 |
35 |
60 |
50 |
60 |
75 |
|
Синергетический эффект действий |
45 |
45 |
70 |
80 |
90 |
70 |
105 |
Тогда, на основе (4) для всех возможных коалиций и случая повторяемости действий могут быть определены значения компонентов вектора Шепли:
1) для коалиции: {m1; m2; m3}
;
;
;
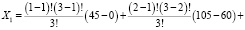
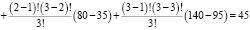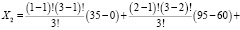
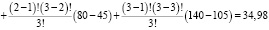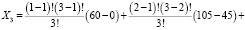
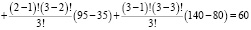2) для коалиции: {m1; m2 }
;
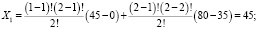
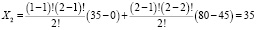3) для коалиции: {m2; m3}
;
;
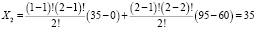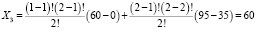4) для коалиции: {m1; m3}
.
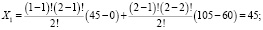
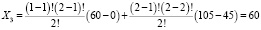Таблица 4
Суммарное значение эффективности для коалиций
|
m1; m2 |
m2; m3 |
m1; m3 |
m1; m2; m3 |
|
|
Значение эффективности для коалиций, E |
80 |
95 |
105 |
139,98 |
В соответствии с тем, что экспертная оценка отражает эффективность МпОБ по отношению к ДД, для анализа результатов и выбора коалиции предлагается использовать условие
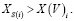(7)
Это связано с тем, что V – это эффективность мероприятия, по постановке задачи требуется выбирать коалицию, максимизирующую эту эффективность. Эффективность коалиции определим как
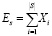. (8)
Теория кооперативных игр допускает введение дополнительных условий и ограничений на выбор оптимальной коалиции. Например, с учетом того, что МпОБ состоит из практических действий, можно учесть невозможность (трудозатратность) реализации всех действий из табл. 1. Значит, при указанных исходных данных требуется выбрать коалицию: {m1; m3}. Это связано с тем, что она имеет максимальное значение Es и не предполагает выполнения всех практических действий из-за чего коалиция {m1; m2; m3} не может быть выбрана.
Аналогичным образом можно воспользоваться теорией кооперативных игр и вектором Шепли для случаев неповторяемости действий и синергетического эффекта действий, а также определить оптимальное сочетание МпОБ и практических действий для всех ДД из (3).
Заключение
Таким образом, теория кооперативных игр и вектор Шепли могут быть использованы для выбора сочетания МпОБ при оценке защищенности системы по отношению к выявленной ДД. Такое применение имеет следующие достоинства:
1) вектор Шепли можно использовать не только для определения справедливого дележа, но и для выбора оптимальной коалиции;
2) возможность учета специфических условий формирования мероприятий (повторяемость и неповторяемость действий);
3) возможность использования различных способов вычисления значений характеристической функции;
4) возможность учета специфических условий оценки эффективности МпОБ (синергетический эффект действий в МпОБ);
5) возможность учета специфических условий формирования коалиций МпОБ (синергетический эффект коалиций);
6) возможность учета различных критериев выбора оптимальной коалиции (максимизация суммарной эффективности коалиции МпОБ, трудозатратность реализации всех действий, выбор коалиции с учетом минимизации избыточности МпОБ по отношению к ДД).