Важную роль выполняет стабилизация качества добытой руды, что влияет на качество товарного концентрата на выходе. Стабилизация качества полезного ископаемого достигается путем усреднения на различных стадиях его добычи, а также в процессе переработки [1, 2]. Построение динамической и непрерывной модели перемешивания, отражающей изменение значения железа и учет временных интервалов, в течение которых поступающая партия полностью вытесняет имеющийся в бункере объем, не проводилось.
После модернизации схемы усреднения на Стойленском ГОК был установлен новый смеситель, при этом объем бункера увеличился в три раза для смешивания трех партий товарного продукта, что позволит получить изменение значения выходного концентрата с меньшей погрешностью, чем при первоначальном объеме бункера. Это связано с тем, что объем потока руды на входе будет вытеснять приблизительно 1/3 объема руды в бункере.
Цель исследования – оценивание эффективности усреднения товарного концентрата руды, базирующегося на применении совокупности предварительно построенных различных математических моделей, позволяющих повысить достоверность результатов и прогнозирования.
Материалы и методы исследования
На Стойленском ГОК для обеспечения однородности химического состава и технологических свойств концентрата в определенном его объеме предусмотрен комплекс технологических и организационных мероприятий, направленных на оценку эффективности усреднения товарного концентрата руды. Был предложен комплексный подход, включающий построение динамической и непрерывной модели перемешивания товарного концентрата, отражающей изменение значения железа и учет временных интервалов, в течение которых поступающая партия полностью вытесняет имеющийся в бункере объем [3].
Для определения «тонких мест» в выполнении процесса стабилизации товарного концентрата и выбора пути решения и прогнозирования процесса усреднения товарного концентрата и поведения системы с помощью компьютерной модели, авторами был использован аппарат системного анализа, включающий принципы: конечной цели, эквифинальности, связности и единства.
Программное обеспечение реализации этого процесса даст возможность сформировать рекомендации по оптимизации параметров процесса усреднения, включающих изменчивость качественных показателей концентрата с не превышающим 0,5 % колебанием массовой доли железа [4] и степенью стабилизации железа на выходе из бункера, которая характеризуется среднеквадратическим отклонением и расходом смеси (коэффициентом вариации).
Авторами предложена комплексная модель процесса механического усреднения, показанная на рис. 1.
До модернизации производственного процесса на Стойленском ГОК применялась одноячеечная модель (идеальная модель в бункере перемешивания). Для идеальной модели перемешивания примем t – идеальное время, при котором новая партия руды вытесняет предыдущую, находящуюся в бункере партию концентрата, при условии, что на выходе получаем показатель концентрата Fe, близкий к значению Fe на входе в бункер на рис. 1. Эти данные влияют на выбор объема бункера перемешивания, что позволит рассчитать средний объем поступающей партии руды.
Одним из условий идеальной модели перемешивания является непрерывность процесса подачи руды в бункер. В середине периода поступления новой партии концентрата значение показателя содержания в руде железа практически не отличается от среднего значения этого показателя на выходе.
Характеристикой идеальной модели является ее дискретность. В связи с требованиями непрерывности к идеальному перемешиванию и допустимо малыми различиями входных и выходных данных поступления железа рассчитывается средневзвешенное значение в бункере в момент завершения поступления новой партии концентрата, что позволило увидеть динамику изменения результирующего значения показателя качества на выходе из смесителя.
Для стабилизации процесса смешивания нужно стремиться к сглаживанию колебаний исследуемого показателя, уменьшению его вариативности, которая характеризуется среднеквадратичным отклонением за конкретный период. Малый объем бункера для смешивания не позволяет оценить точность прогноза. Увеличение же объема бункера позволит повысить эффективность усреднения товарного концентрата руды за счет оценки точности прогноза.
Новая прогнозная модель разрабатывается на основе ячеечной модели, которая состоит из отдельных ячеек, представляющих собой модель идеального перемешивания. В предлагаемой математической модели, включающей совокупности дифференциальных уравнений, описывающих динамическую и непрерывную модели перемешивания товарного концентрата с изменяющимися условиями, применяется процедура расчета скользящего средневзвешенного среднего для сглаживания и оценки точности прогноза.
Набором данных выступает количество железа в руде, загруженное в бункер. В математической модели авторами рассмотрены данные по железу, которые последовательно организованы в ряд через равные промежутки времени, и этот ряд рассматривался как временный. Характеристиками временного ряда выступают средний период и частота колебаний, коэффициент усреднения для идеального аппарата и коэффициент усреднения для многоячеечного аппарата.
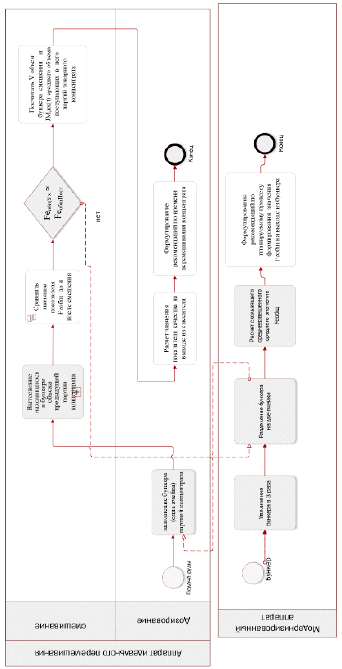
Рис. 1. Комплексная модель процесса механического усреднения
Таким образом, для прогнозной модели моделируются временной ряд и прогноз. На первом этапе определяется обозначение периодов через ti и вводится лаг, равный первым трем поступающим в бункер партиям концентрата. На втором этапе вычисляется средневзвешенное значение выходного железа. Завершается расчет средневзвешенным значением с учетом лага, при этом в качестве предыдущего значения бралось 2/3 от суммарного объема находящейся до момента поступления новой партии в бункере массы концентрата.
Входная ошибка (остаток) влияет на выходной объем железа при условии, что в бункере объемный расход концентрата и объем концентрата постоянный; значения железа на выходе и в самом бункере равны, и таким образом выполняются условия квазистационарности.
Таким образом будет формироваться ряд данных по железу на выходе из бункера.
Для формирования начальных данных определяются на входе и выходе концентрации вещества на основании уравнения материального баланса [5]:
VfM(t) = c × kвх(t), (1)
VgM(t) = c × kвых(t), (2)
где c – расход смеси, м3; M – вес руды; kвх(t) – концентрация железа на входе; kвых(t) – концентрация железа на выходе; VB – объем бункера, м3; Vf (t) – входной объем руды; Vg(t) – выходной объем руды.
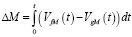, (3)
где ΔM – изменение веса руды в бункере от 0 до t.
Учитывая то, что вес руды в бункере равен на входе и выходе и определяется по формулам (1), (2),
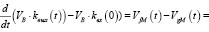
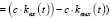, (4)
при t = 0, с = const следует, что
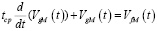, (5)
tcp = VB / v, где tcp – среднее время процесса смешивания в бункере, VB – объем аппарата, v – объемный расход смеси.
Уравнение (5) является математической моделью для идеального аппарата смешивания, при условии VgM(t) = W = const.
В связи с тем, что в аппарате идеального смешивания рассматривается ступенчатое воздействие, в математической модели kвх(t) показывается мгновенное изменение входного значения железа на конечное:
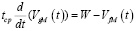. (6)
Данное уравнение решается разделением переменных:
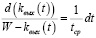. (7)
Проинтегрировав (7) и после этого, определив постоянную интегрирования из начальных условий: при t = 0, kвх(t) = 0 и получив -ln(W) = ln(D). Далее, подставляя в уравнение (7) постоянную интегрирования и проведя потенцирование, получается
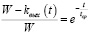. (8)
В результате разработана математическая модель концентрации железа на выходе:
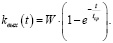(9)
Из (9) следует, что среднее время пребывания массы вещества в бункере является одной из определяющих характеристик аппарата идеального смешивания, которая вычисляется из кривой разгона. Чтобы проанализировать поведение математической модели, (9) следует преобразовать по Лапласу:
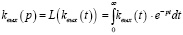,(10)
где e–pt – ядро преобразования; kвых(t) – преобразуемая функция – оригинал; kвых(р) – преобразованная функция – изображение.
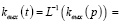
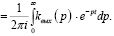(11)
Выразим через передаточную функцию входной параметр концентрации [6]:
kвых(р) = R(р) kвх(р), (12)
где R(р) – передаточная функция.
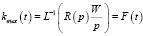, (13)
где F(t) – кривая разгона перемешивания в бункере.
F(t) равна изменению во времени выходной характеристики концентрата при поступлении на вход единичного ступенчатого возмущения: kвх(t) = W = const.
То, что на предприятии проведена модернизация и объем бункера увеличился в три раза, повлияло на эффективность смешивания руды в бункере. Для многоячеечного аппарата предлагается скорректировать математическую модель аппарата идеального смешивания.
При увеличении объема бункера перемешивания в n раз необходима дополнительная корректировка модели. Для нахождения прогнозной модели СКО предлагается использовать ячеечную модель, основанную на предположении об идеальном перемешивании в пределах ячеек, расположенных последовательно, и отсутствии перемешивания между ячейками [6].
Параметром, характеризующим модель, служит количество ячеек n. Если математическое описание модели идеального перемешивания n последовательно поступающих в смеситель партий представляло собой последовательность n линейных дифференциальных уравнений первого порядка, то описание ячеечной модели предполагает разбиение бункера на две одинаковых по объему ячейки и представляет последовательность дифференциальных уравнений. Например, процесс смешивания в двухъячеечном бункере зависит от фиксированного времени при выходе из первой ячейки и входе во вторую ячейку. Значение товарного концентрата железа во второй ячейке будет эквивалентно значению железа после заполнения половины первой ячейки новой массой вещества. При фиксированном времени, при котором каждые четыре часа руда поступает в бункер, для анализа количества железа в массе руды используется ступенчатое воздействие. Но поскольку имеется две ячейки, то изменяется как объем вещества, так и концентрация параметра качества железа в руде.
Начальным условием для этой модели выступает уравнение, показывающее значение концентрации железа на выходе из бункера, равное начальной концентрации железа в общей массе руды:
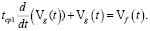(14)
Математическая модель прогноза изменения показателя качества выходного концентрата железа, после смешивания в n партий руды, вычисляется последовательностью дифференциальных уравнений:
, 
;
, 
;…
, 
;
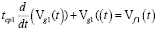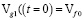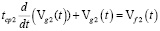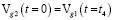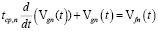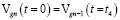где t4 – конечное время.
Ряд данных состоял из 40 значений концентрации железа на входе во вторую ячейку Vn,2. Далее для каждой концентрации получаем
; 
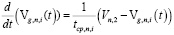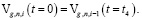(15)
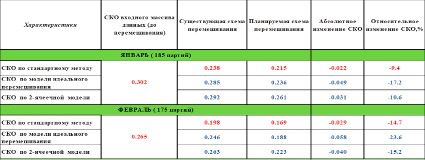
Рис. 2. Среднеквадратичное отклонение по стандартному методу, моделям идеального перемешивания и двухъячеечной модели
Для решения дифференциальных уравнений в прикладном пакете Matlab R21b была составлена программа, которая формирует выходные данные концентрации железа с шагом 0,1 ч и статистические характеристики временного ряда. С помощью этой компьютерной модели рассчитаны и показаны дополнительные оценки прогнозного значения среднеквадратичного отклонения в бункере. Предлагаемая подсистема позволила дополнительно оценить абсолютные и относительные изменения значения среднеквадратичного отклонения данных в бункере. Прогнозная оценка различных характеристик массива данных формируется за весь исследуемый период. Фрагмент за январь и февраль приведен на рис. 2.
Для существующей схемы смешения в двухъячеечной модели среднеквадратическое отклонение в среднем выше на 6 %, чем с использованием модели идеального перемешивания, а для схемы, планируемой к внедрению, в среднем на 15 %.
Таким образом, прогнозные показатели качества товарного концентрата двухъячеечной модели наиболее точно отражают реальный характер процесса перемешивания в результирующей смеси бункера.
С помощью разработанных имитационных моделей был спрогнозирован оптимальный объем бункера и предложены рекомендации по подбору параметров и характеристик системы перемешивания для достижения оптимальной экономической обоснованности.