Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Одним из приоритетных направлений федерального стандарта основного общего образования является формирование функциональной грамотности обучающихся. В состав функциональной грамотности входит математическая грамотность. Проблема формирования математической грамотности рассматривается в работах Л.О. Рословой, Е.С. Квитко, И.И. Карамовой [1], И.И. Валеева [2], Н.В. Дударевой и Е.А. Утюмовой [3] и др. В настоящее время, как показывает практика обучения в школе, обучающиеся основной школы испытывают трудности в изучении математики и применении полученных знаний на практике, тогда как математические знания, умения и навыки необходимы в различных сферах человеческой деятельности, в том числе в научно-технических исследованиях прикладной направленности в цифровом пространстве и приоритетных направлениях социально-экономического развития. Поэтому проблема формирования математической грамотности обучающихся является особенно актуальной. При ее реализации особую роль играет применение практико-ориентированных задач, которые нацелены на формирование у учащихся практических навыков использования математических знаний и умений, необходимых в повседневной жизни. Включение практико-ориентированных задач при изучении разных тем школьного курса математики не является совершенно новым. Из опыта таких исследователей, как Г.А. Пожарова [4], А.Д. Нахман [5], А.И. Мингулова [6] и др., следует, что такой подход помогает обучающимся осознать реальные практические задачи, решение которых требует математических знаний и навыков.

Цель исследования – теоретически обосновать и экспериментально проверить влияние разработанного комплекса практико-ориентированных задач с этнокультурным содержанием в школьный курс математики на уровень сформированности математической грамотности обучающихся 8 класса.

Материалы и методы исследования

В данном исследовании, прежде всего, проясним значения таких понятий, как «грамотность» и «функциональная грамотность». Понятие «грамотность» исторически менялось в зависимости от базовых показателей социально-культурного развития общества, от умения только писать, читать и считать до владения минимумом общественно необходимых знаний и навыков, которые впоследствии были названы функциональной грамотностью. Н.Н. Сметанникова, исследуя данное понятие, пишет, что «грамотность – это базовая учебная компетенция, позволяющая человеку непрерывно учиться и осваивать новое, получать доступ к богатствам мировой и национальной культуры и тем самым расширить свой внутренний мир. Способность и готовность человека к активному усвоению знаний и их применению в каждодневной жизни» [7]. На данном этапе развития российского образования формирование функциональной грамотности обучающихся основной школы определяется как формирование «способности решать учебные задачи и жизненные проблемные ситуации на основе сформированных предметных, метапредметных и универсальных способов деятельности» [8, с. 29]. В нашем исследовании будем считать понятия «математическая грамотность» и «функциональная математическая грамотность» эквивалентными.

В исследованиях Л.О. Рослова, Е.С. Квитко, И.И. Карамова [1] понятие «математическая грамотность» рассматривается как «способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира». В своей работе Н.В. Дударева, Е.А. Утюмова [3] при создании структурно-логической модели как основы для разработки методики обучения математике, способствующей формированию математической грамотности обучающихся, выделили компоненты математической грамотности (когнитивный, деятельностный, прогностический и рефлексивный). В настоящем исследовании условимся исходить из мнения И.И. Валеева [2, с. 355], что математическая грамотность – это «способность человека выявлять и понимать роль математики в окружающем мире, высказывать математические суждения и использовать математику так, чтобы удовлетворить потребности, свойственные созидательному и мыслящему гражданину».

Анализ научно-методической литературы позволяет выделить различные методы формирования математической грамотности, основанные на применении устных упражнений высокого уровня сложности или многотипных разноуровневых заданий, построенных на одном жизненном сюжете, учебно-исследовательской или проектной деятельности и т.д. При всем разнообразии методов их формирования многие исследователи [4–6; 9] обосновывают роль практико-ориентированных задач формированием умения решать реальные жизненные и практические задачи с помощью математических знаний, выражением связи математики с реальностью и в демонстрации ее применения в повседневной жизни.

В исследовании использованы такие методы, как теоретический анализ научно-методической литературы, эмпирический анализ собственного педагогического опыта, педагогический эксперимент.

Результаты исследования и их обсуждение

Математика является языком современной науки, поэтому роль математического образования в современном мире очень велика. Работа с практико-ориентированными задачами помогает обучающимся лучше усваивать материал и получать первичный опыт использования математических знаний в повседневной жизни, что способствует повышению их уровня математической грамотности. Практико-ориентированные задачи могут включать в себя задачи на покупки, расчеты по строительству дома или сада, определение расходов на топливо и т.д. Они позволяют ученикам проявлять свои знания в реальных ситуациях и научиться применять их для решения конкретных задач. Стоит отметить, что примером для формирования математической грамотности также служат задачи с этнокультурным содержанием, которые помогут обучающимся не только применять свой жизненный опыт, но и усваивать духовные, нравственно-этнические ценности, которые были накоплены веками.

В рамках исследования разработан комплекс практико-ориентированных задач с этнокультурным содержанием для обучающихся 8 класса. Задачи классифицированы по всем темам учебника С.М. Никольского. Приведем примеры разработанных заданий по двум темам: «Числовые неравенства», «Решение задач с помощью рациональных уравнений» и «Равномерное движение».

При изучении первой темы на разных этапах урока предлагались обучающимся следующие задачи:

1. Жители Якутии живут в суровых условиях, и, чтобы сохранять свое здоровье, они придерживаются здорового образа жизни, включая активность и правильное питание. Для того чтобы сохранить здоровье, обычным людям необходимо проходить в среднем не менее 10 тыс. шагов в день. Профессиональным охотникам или рыбакам, которые постоянно находятся на улице, рекомендуется делать не менее 20 тыс. шагов в день. Пусть X – количество шагов, которое делает рыбак ежедневно, Y – количество шагов, которое делает обычный житель Якутии. Необходимо написать и решить числовое неравенство, которое будет учитывать наши условия: обычный житель Якутии должен делать не менее 10 тыс. шагов в день, а если житель является профессиональным рыбаком, то он должен делать не менее 20 тыс. шагов в день. Найдите интервалы, в которых могут находиться значения X и Y. Если рыбак сделал 18 тыс. шагов в день, а обычный житель – 12 тыс. шагов, то кто из них ведет более активный образ жизни?

2. В Якутии часто проводятся соревнования на метание якутского ножа. Одна из традиционных дисциплин – это метание ножа на определенное расстояние. Предположим, что опытные метатели якутского ножа могут попасть в цель на расстоянии до 15 м, начинающие – на расстоянии до 10 м. Чтобы считаться профессионалом в метании якутского ножа, необходимо попадать в цель не менее чем на расстоянии 12 м. Напишите числовое неравенство, которое отражает данную ситуацию. Найдите интервалы, в которых могут находиться значения расстояния, на которое могут бросать якутский нож опытные и начинающие метатели. Если один из участников соревнования метнул нож на расстояние 13 м, то является ли он профессионалом?

3. Жители Якутии очень любят традиционные зимние виды спорта, такие как коньки, лыжи и сноубординг. Однако, чтобы пойти на каток или лыжню, нужно учитывать погодные условия. Для безопасного катания на коньках или лыжах температура на улице должна быть выше -30 °C. При этом, если ребята надевают теплую одежду и катаются не более часа, оптимальная температура для катания не должна превышать -5 °C. В Якутске на улице сегодня утром было -30 °C. Школьники хотят пойти кататься на коньках на каток, но некоторые родители считают, что это слишком холодно. Какие температуры на улице будут безопасны для катания на коньках, если ребята надевают теплую одежду и катаются максимум час? Напишите числовое неравенство для решения этой задачи.

На уроке при изучении темы «Решение задач с помощью рациональных уравнений» обучающимся была предложена следующая задачная ситуация:

Отель представляет разные программы экскурсий для своих посетителей. Одна из программ предполагает посещение трех музеев в разных частях города за один день. Для того, чтобы охватить все музеи, группа экскурсантов должна перемещаться на общественном транспорте. Ресурсом таксопарка является система электронных браслетов, которую можно использовать для оплаты поездок. Стоимость поездки на такси зависит от расстояния и времени в пути. Программа экскурсии предполагает следующие маршруты:

− Музей изобразительных искусств, который находится на расстоянии 10 км от отеля. Стоимость поездки на такси до него составляет 500 руб., если на маршруте будет 4 пассажира, и 600 руб., если будет 5 пассажиров.

− Археологический музей, который находится на расстоянии 7 км от первого музея и 6 км от отеля. Стоимость поездки на такси в любом случае составит 400 руб., если на маршруте будет 4 пассажира, и 500 руб., если будет 5 пассажиров.

− Музей истории, который находится на расстоянии 9 км от второго музея и 8 км от отеля. Стоимость поездки на такси в любом случае составляет 450 руб., если будет 4 пассажира, и 550 руб., если будет 5 пассажиров.

Определите, какое количество пассажиров должно быть в группе экскурсантов, чтобы минимизировать затраты на поездки на такси. Составьте рациональную функцию, которая определяет стоимость проезда в зависимости от количества пассажиров. Решите уравнение и найдите количество пассажиров, при котором стоимость поездок будет минимальной.

При изучении темы «Равномерное движение» предлагались следующие задачи:

1. В Северной Якутии на протяжении зимнего периода перемещаются на собаках-хаски для охоты и сбора необходимых ресурсов. Регулярные вылазки на собачьих упряжках требуют знания расстояний и времени движения. Алексей отправляется на собачьей упряжке к стоянке. Он движется равномерно со скоростью 15 км/час. Постройте график пути равномерного прямолинейного движения. Сколько минут ему потребуется на дорогу в одну сторону, если путь составляет 24 км?

2. У каждого охотника-промысловика есть свои охотничьи угодья, и в их пределах он имеет несколько избушек-стоянок. Охотник-промысловик едет на собачьей упряжке от одной стоянки до другой, которая находится в 28 км от первой. Первые 5 км едет со скоростью 5 км/ч, в последующем (кроме последнего отрезка пути) каждые 5 км едет со скоростью на 5 км/ч больше предыдущей. И максимальная скорость на последнем отрезке пути 25 км/ч. Найдите среднюю скорость движения на протяжении всего маршрута.

Экспериментальная работа проведена в МОБУ «Тулагинская СОШ им. П.И. Кочнева» г. Якутска РС (Я). В 2022–2023 учебном году в 8 «а» класса 24 обучающихся, а в 8 «в» 25 обучающихся. На констатирующем этапе эксперимента проводилась диагностическая работа из открытого банка заданий [10]. В табл. 1 представлены результаты сформированности математической грамотности обучающихся 8 класса.

Анализ результатов диагностической работы позволяет сделать следующие выводы: 1) более 85 % испытуемых показали средний уровень сформированности математической грамотности; 2) участники диагностической работы лучше всего справляются с заданиями, связанными с чтением и интерпретацией данных; 3) отмечается недостаточность знаний обучающихся в выполнении заданий, связанных с применением математических формул, с распознаванием и интерпретацией зависимостей; 4) у обучающихся есть затруднения в выделении главного вопроса в задаче и записи ответа.

По результатам диагностической работы в качестве экспериментальной группы был избран 8 «в» класс, в качестве контрольной – 8 «а».

Таблица 1

Результаты диагностической работы на констатирующем этапе

Таблица 2

Результаты диагностической работы на контрольном этапе

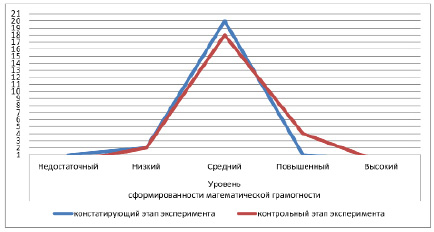
Сравнительный анализ сформированности математической грамотности обучающихся экспериментального класса

На формирующем этапе исследования в экспериментальной группе была проведена целенаправленная работа с применением составленного комплекса заданий. В табл. 2 представлены результаты второй диагностической работы [10], проведенной на контрольном этапе экспериментальной работы.

Достоверный рост сформированности математической грамотности обучающихся был подтвержден с помощью Т-критерия Вилкоксона. «Типичный» сдвиг является достоверно преобладающим по интенсивности, так как Tэмп = 21 ниже T0,01 = 43 при n = 20.

Анализ результатов исследования показал, что решение практико-ориентированных задач с этнокультурным содержанием повышает уровень сформированности математической грамотности обучающихся.

Заключение

В ходе исследования изучены теоретические основы формирования математической грамотности обучающихся основной школы, разработан комплекс практико-ориентированных задач для обучающихся 8 класса, которые классифицированы по темам учебника С.М. Никольского, и проведена апробация составленного комплекса задач. Проведенное исследование, теория и практика, запросы и вызовы реальной жизни показывают, что центральную роль в успешности формирования математической грамотности играют практико-ориентированные задачи.