Не секрет, что у современного школьника изучение геометрии вызывает значительные трудности. Учащиеся не любят и не понимают этот предмет, что подтверждает хотя бы то, что средние баллы за геометрические задания выпускных экзаменов последних лет традиционно оказываются самыми низкими среди всех баллов ОГЭ и ЕГЭ по математике. Причин этому может быть несколько, одна из которых – недостаточная эффективность современных методик и технологий обучения. В условиях сегодняшней загрузки учителей и учеников, приводящей к дефициту учебного времени, для повышения качества геометрического образования учащихся, на наш взгляд, имеет смысл обратиться к технологии укрупнения дидактических единиц (УДЕ) [1; 2]. Эта технология предполагает переструктурирование изучаемого материала и его группирование в крупные блоки, что способствует более прочному, осознанному и качественному восприятию обучаемыми содержания учебного предмета при меньших временных затратах. Значит, зародившись в 1960-х гг. эта технология не потеряла актуальности и сегодня.
В практике обучения в российских школах технология УДЕ до сих пор многими учителями нередко воспринимается как новаторская, инновационная технология обучения, так как они в лучшем случае слышали о ней, но не владеют достаточными навыками использования ее приемов и средств обучения. В связи с этим уже на этапе подготовки будущих учителей-предметников в педвузах необходимо организовывать специальную методическую подготовку слушателей к обучению учащихся геометрии в контексте УДЕ.
Целью исследования стал поиск и разработка средств методической подготовки студентов-математиков педвуза к обучению учащихся геометрии в контексте укрупнения дидактических единиц.
Материалы и методы исследования
Методами исследования явились: изучение научной и учебно-математической литературы, педагогическое моделирование, анализ и обобщение педагогического опыта преподавателей геометрии, обработка результатов исследования. Материалы исследования могут быть интересны как преподавателям педагогических вузов, так и учителям математики.
Результаты исследования и их обсуждение
Основным видом деятельности в изучении математики выступает решение задач. Через него учащийся познает изучаемый предмет, а учитель осуществляет достижение образовательных целей. В нашем исследовании задача должна не только быть носителем предметного содержания математики, но отражать методический характер подготовки студентов педвуза к будущей профессии. Поэтому, на наш взгляд, основным средством подготовки студентов-математиков педвуза к обучению учащихся геометрии в контексте УДЕ будет выступать методическая задача. Методическая задача есть предметно-содержательная модель деятельности учителя и/или учащихся, построенная для достижения конкретных учебных целей, обусловленных предметным содержанием. Данная модель представляет собой систему М = {A; B}, где А – предметная составляющая содержания частных учебных задач, В – методическая составляющая решения частных учебных задач. Компоненты А и В данной системы М представляют собой множество элементов, также взаимосвязанных между собой через некоторые свойства и отношения так, что образуется система. В частности, в обучении геометрии:
− компонент А включает в себя элементы предметного математического содержания, связи и отношения между ними (математические понятия, теоремы, задачи, методы решения задач и т.д.);
− компонент В включает в себя дидактические приемы преподавателя (предъявление плана, демонстрацию образца, постановку вопросов и др.), действия учащихся по решению частных учебных задач, а также различные методические понятия и термины (интеграция, деятельностный подход, методика решения задачи, формирования понятия, работы с теоремой и т.д.).
В подготовке будущих учителей геометрии к обучению учащихся в контексте УДЕ можно использовать разные виды соответствующих методических задач [3]. В частности, это зависит от того, какое из двух основных направлений такой подготовки реализуется в практике обучения студентов:
1) фрагментарная методическая подготовка при изучении математических дисциплин в педвузе;
2) целенаправленная систематическая методическая подготовка при изучении специального курса.
Наибольшими возможностями для реализации первого направления на математических факультетах педвуза, на наш взгляд, обладает курс элементарной математики [4]. Он является хорошей площадкой для интеграции школьных и вузовских математических дисциплин в педвузе, а также вузовских дисциплин методической направленности.
Например, после решения студентами на занятиях по элементарной математике нескольких геометрических задач с помощью метода поворота им можно предложить следующие методические задачи 1.1–1.4.
1.1. На основе анализа решенных Вами математических задач, перечислите действия дi (i∈N), адекватные методу поворота.
1.2. Укажите алгоритм решения задач с помощью метода поворота. Обобщите его до алгоритма решения задач методом геометрических преобразований.
1.3. На основе одной из решенных Вами задач составьте систему задач зi (i∈N) для обучения учащихся методу поворота в соответствии со следующими принципами:
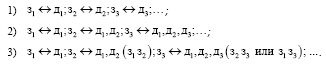
Учитываются ли какие-либо из данных принципов взаимосоответствия между задачей и действиями, адекватными методу ее решения, авторами школьных учебников при разработке последних?
1.4. Подберите задачи, направленные на обучение учащихся интеграции метода поворота и других методов (одного или нескольких) решения задач по геометрии. Ответ поясните.
Выполнение студентами приведенной серии методических задач 1.1–1.4 способствует видению ими деятельностной основы обучения учащихся в контексте технологии УДЕ, восприятию ими средств и методов соответствующего обучения учащихся, осознанию методической составляющей школьного курса геометрии и т.д.
Также при формировании у студентов-математиков методических умений по обучению учащихся геометрии в контексте УДЕ большими возможностями обладают не только серии методических задач, но и блоки укрупненных математических задач, интегрированные с методическими заданиями. Такие блоки направлены на понимание студентами предметного содержания решаемой математической задачи, воспринимаемого сквозь призму методического содержания. Для демонстрации сказанного обратимся к блоку взаимосвязанных задач 2.1–2.4.
2.1 В прямоугольник АВСD вписаны два квадрата EFGM и MGNK так, как показано на рис. 1, А. Докажите, что точки A, E, G и K лежат на одной окружности. Представьте ваши рассуждения по решению данной задачи в виде граф-схемы.
2.2 Квадраты EFGM и MGNK расположены внутри прямоугольника ABCD так, как показано на рис. 1, А. Вычислите угол АРВ. Поясните эстетический компонент выбранного вами способа решения.
2.3 На рис. 1, А, ABCD – прямоугольник, EFGM и MGNK – квадраты. Определите, в каком отношении АР делит площадь прямоугольника ABCD, если АВ = 6, AD = 8. Перечислите общие действия, адекватные решению данной задачи. Установите зависимость между данной задачей и решенными ранее задачами 2.1 и 2.2. Выделите прием, с помощью которого составлены задачи 2.2 и 2.3 на основе предыдущей.
2.4 Составьте и решите задачу, обратную к задаче 2.3.
При решении задачи 2.1 в процессе математических рассуждений (развитии математической компоненты методической подготовки обучаемых) у студентов одновременно происходит и развитие методической компоненты их подготовки (табл. 1).
Развивая математическую компоненту в контексте выбранного второго направления решения задачи 2.1, нетрудно заметить, что если EM = МK, то М – середина гипотенузы прямоугольного DАЕК, значит, АМ = ЕМ = КМ как радиусы описанной около него окружности. Тогда АМ = ЕМ = GM = КМ, то есть точки A, E, G и K действительно лежат на одной окружности, центр которой расположен в точке М.
Развивая методическую компоненту, студенты, выполняя явное задание методического характера (сформулированное в тексте задачи 2.1 и направленное на формирование у будущих учителей математики умений составлять и использовать в обучении учащихся одного из средств обучения в контексте УДЕ – граф-схем [5]), могут представить наглядную схему (рис. 2), на основании которой также становится очевидным план решения задачи 2.1.
При решении задачи 2.2 студенты первоначально могут обосновать, что точки A, E, G и K лежат на одной окружности. То есть фактически выполнить те же действия (повторить проведенные ранее рассуждения), что и при решении задачи 2.1. Далее, учитывая, что центр этой окружности – точка М, можно сделать вывод, что ∠GМK – центральный, причем опирается на ту же дугу GК, что и вписанный ∠GАK. Значит,
∠GAK = 1/2 ∙ ∠GМK = 1/2 ∙ 90° = 45°.
Отсюда ∠ВРА = 45° как накрест лежащий с ∠GAK.
При работе с задачей 2.2 студенты, раскрывая ее методическую сторону через выполнение соответствующего методического задания, приходят к выводу, что эстетичность задачи 2.2 может быть обоснована появлением в решении окружности, о которой первоначально в ней ничего не говорилось. Эффект неожиданности, а также краткость решения демонстрируют красоту геометрических объектов и геометрии в целом [6].
Таблица 1
Математические и методические компоненты методической подготовки студентов при решении задачи 2.1
|
Компонент А (предметное содержание) |
Компонент В (методическое содержание) |
|
Пусть точки A, E, G и K лежат на одной окружности (рис. 1, Б). Следовательно: 1) эта окружность описана около четырехугольника AEGK; 2) точки A, E, G и K расположены на одном расстоянии от некоторой точки – центра этой окружности |
Получение предварительной информации об объекте, выведение следствий из факта принадлежности объекта понятию |
|
Если около четырехугольника AEGK описана окружность, то ∠EAK + ∠EGK = 180° (или ∠AEG + ∠AKG = 180°). Значит, надо найти градусные меры двух противоположных углов четырехугольника AEGK и сложить их. Если точки A, E, G и K расположены на одном расстоянии от некоторой точки (которая будет центром окружности), то они будут концами четырех равных отрезков с общим концом, который в этом случае совпадет с центром этой окружности, а сами отрезки будут ее радиусами. Значит, надо искать равные отрезки, расположенные соответствующим образом |
Планирование будущей деятельности, выдвижение гипотезы |
|
По условию задачи очевидно, что ∠EAK = 90° и EM = GM = KM как стороны квадратов EFGM и MGNK. То есть, двигаясь в первом направлении, нам достаточно найти ∠EGK. А двигаясь во втором направлении, доказать, что хотя бы один из отрезков EM, GM или KM равен отрезку АМ. Отсюда оба обозначенных направления равновозможные. Но так как второе направление дает нам больше оснований для развития темы задачи 4.1 (информации о задачной ситуации), позволяя увидеть еще и центр исследуемой окружности, то мы остановимся на этом направлении |
Направленность на поиск нового, более информативного способа решения, объяснение выбора направления решения задачи, выбор основания прогнозирования |
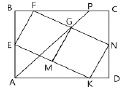
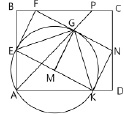
А) Иллюстрация к условию задачи 2.1 Б) Иллюстрация к решению задачи 2.1
Рис. 1. Иллюстрации к задаче 2.1
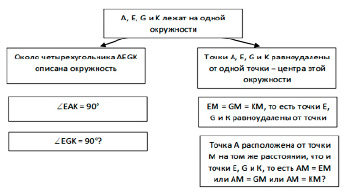
Рис. 2. Граф-схема, иллюстрирующая анализ задачи 2.1
Таблица 2
Действия, адекватные решениям задач 2.1–2.3
|
Задача 2.1 |
Задача 2.2 |
Задача 2.3 |
|
Докажем, что около четырехугольника AEGK можно описать окружность |
||
|
Докажем, что ∠ВРА = 45° |
||
|
Вычислим площадь равнобедренного и прямоугольного DАВР как половину произведения его катетов Вычислим площадь прямоугольника ABCD как произведение его смежных сторон Найдем отношение площади DАВР к площади прямоугольника ABCD |
||
Задача 2.3, в свою очередь, укрупняет решение задачи 2.2, как можно видеть из табл. 2. На основании этой таблицы можно утверждать, что з4.1 → з4.2 → з4.3. При этом задача 2.2 получена на основе задачи 2.1 посредством замены требования последней при сохранении условия. Задача 2.3 получена из задачи 2.2 также посредством постановки нового требования, но при одновременном сохранении и расширении исходного условия. Осознание данных взаимосвязей между задачами способствует пониманию студентами оснований конструирования таких средств обучения учащихся в контексте технологии УДЕ как блоков взаимосвязанных задач [5].
При решении задачи 2.4 студенты знакомятся с таким приемом методической деятельности по обучению учащихся геометрии в контексте УДЕ как преобразование математической конструкции (задачи) посредством ее обращения.
Некоторые методические задачи, аналогичные приведенным выше, использовались нами в собственной практике обучения студентов-математиков педвузов. Как показывали текущие занятия со студентами и результаты контролирующих мероприятий, работа с такими задачами достаточно эффективно способствовала пониманию обучаемыми изучаемого предметного математического содержания (что также важно для учителя), а также – понимания специфики методики обучения учащихся предметному содержанию в контексте УДЕ [7].
Заключение
Итак, на основании проведенного исследования можно утверждать, что основным средством методической подготовки студентов-математиков педвуза к обучению учащихся геометрии в контексте укрупнения дидактических единиц выступают методические задачи. Через работу с ними будущие учителя математики приходят к пониманию возможностей разных средств обучения учащихся в контексте УДЕ: граф-схем, блоков укрупненных задач и др. При работе с такими задачами можно использовать разные специальные приемы обучения (исследования выполненных решений задач, поиска векторов развития темы задачи, установления связей между компонентами предметного содержания и др.) и формы обучения студентов (организации самостоятельного решения блоков задач студентами, составления новых задачных блоков, граф-схем и др.). Все это вкупе эффективно способствует становлению будущих учителей математики как активного пользователя технологии укрупнения дидактических единиц.
Исследование проведено в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов-партнеров ФГБОУ ВО «Мордовский государственный педагогический университет им. М.Е. Eвсевьева» и ФГБОУ ВО «Чувашский государственный педагогический университет им. И.Я. Яковлева» по теме «Обучение геометрии учащихся общеобразовательных учреждений в контексте укрупнения дидактических единиц».



