Инвариантность в математике – это свойство математического объекта оставаться неизменным после операции или трансформации определенного типа. Теория инвариантов может быть использована как удобный язык для решения задач, связанных с алгебраическими преобразованиями. Один из первых алгебраических инвариантов Лагранжа – дискриминант квадратичной формы. В случае бинарной формы 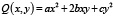 он вычисляется по формуле
он вычисляется по формуле 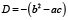 и используется при нахождении корней квадратных уравнений. В информатике – это логические утверждения, которые считаются истинными на определенном этапе исполнения программы. Они эффективны, например, при решении задачи об эквивалентности объектов, описанных графами [1].
и используется при нахождении корней квадратных уравнений. В информатике – это логические утверждения, которые считаются истинными на определенном этапе исполнения программы. Они эффективны, например, при решении задачи об эквивалентности объектов, описанных графами [1].
Представляют интерес вопросы применения инвариантов в задачах контроля работоспособности технических систем. В качестве инвариантов здесь могут выступать устойчивые корреляционные связи между показаниями датчиков. Они помогают проводить восстановление и эмуляцию данных [2]. В свою очередь, отсутствие подобной корреляции в процессе функционирования свидетельствует о сбое или выходе датчика из строя.
В диагностике технических систем нашли применение сети инвариантов [3]. Их объединение по наблюдаемым компонентам и проведение корреляционного анализа позволяет обнаруживать аномальное поведение системы по отклонениям. Аналогичный подход, но применительно к анализу программного обеспечения рассмотрен в работах [4, 5]. В качестве недостатка этого направления можно назвать сложность определения инвариантов, фильтрации данных и обнаружения ложных срабатываний. Большую практическую значимость имеют алгебраические инварианты. Примером служат такие инвариантные моменты, как преобразователи «изображение – код» для бинарных и полутоновых изображений, выражаемые полиномами. На основе комбинации алгебраических инвариантов, составляющих определенный базис, можно строить другие инварианты в виде некоторых многочленов [6]. В теории систем управления инварианты активно применяют для анализа динамических систем и синтеза систем управления с заданными характеристиками. Так, например, в качестве инвариантов часто выделяют эллипсоиды, связанные с функциями Ляпунова [7].
Таким образом, понятие инвариантов широко используется в различных областях математики, техники, информатики и автоматического управления. Следует отметить, что представленный обзор может быть дополнен и другими примерами выявления устойчивых свойств объектов, называемых инвариантами или субинвариантами, которые могут быть успешно применены, например, в задачах распознавания образов и выявления состояний объектов различной природы [8].
Работа направлена на исследование характеристик различных динамических систем, остающихся неизменными, т.е. инвариантов к определенным преобразованиям. Целью работы является применение теории инвариантов в некоторых задачах управления техническими системами. В качестве практических примеров предлагается исследовать инварианты передаточных функций замкнутой системы автоматического управления и рассмотреть решение задачи преследования-убегания, для которой поставлено условие встречи игроков на заданном эллипсе, являющимся в свою очередь геометрическим инвариантом.
Материалы и методы исследования
Пусть задано множество М, на котором определены преобразования G. Исходя из свойств инвариантности, можно записать: 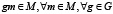 [9]. Представляет интерес вопрос о полноте набора независимых инвариантов для множества M и их количестве. Введем некоторые определения, связанные со свойствами инвариантности.
[9]. Представляет интерес вопрос о полноте набора независимых инвариантов для множества M и их количестве. Введем некоторые определения, связанные со свойствами инвариантности.
Определение 1. Набор инвариантов φ1,…,φN называется полным, если из равенства инвариантов двух произвольных элементов множества M следует их эквивалентность 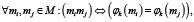
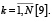
Определение 2. Полная система инвариантов называется минимальной, если из нее нельзя удалить ни одного инварианта, не нарушая полноты.
Инварианты передаточных функций (инварианты статической обратной связи)
Рассмотрим устойчивость параметров управления к действию статической обратной связи на основе анализа передаточной функции замкнутой системы. Пусть задан объект управления с передаточной функцией вида
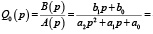
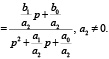 (1)
(1)
Передаточная функция замкнутой системы (1) определяется в соответствии с поясняющей схемой, представленной на рис. 1.
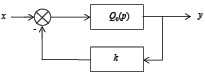
Рис. 1. Замкнутая система управления
В соответствии с рисунком получаем
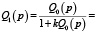
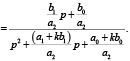 (2)
(2)
Матрицы коэффициентов передаточных функций Q0(p) и Q1(p) имеют вид
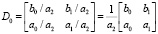 . (3)
. (3)
Коэффициенты числителя передаточной функции замкнутой системы в количестве n не изменили своего значения. Корни полинома B(p) (нули системы) также не изменились, т.е. являются инвариантами.
Задача поиска дополнительных инвариантов сводится к анализу унипотентного преобразования. В нашем случае применяя матрицу преобразования
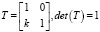 , (4)
, (4)
получим матрицу D1 = TD0,
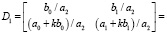
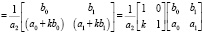 .
.
Инвариантами, кроме элементов первой строки матриц D, являются её миноры второго порядка
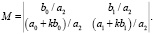 (5)
(5)
Таким образом, имеем характеристики динамических систем, остающиеся неизменными, т.е. инварианты к рассмотренному преобразованию Q1(p).
Рассмотренный подход является демонстрацией успешного выявления инвариантных особенностей системы управления, определяющих ее устойчивость к изменениям выхода.
Эллипсы как инварианты в системах управления
Рассмотрим один из вариантов решения задачи преследования-убегания. Известные задачи преследования, когда скорость преследователя больше скорости убегающего, приводят к встрече убегающего и преследователя на границе окружности или поверхности сферы Аполлония [10].
В нашем случае задача заключается в подборе управления таким образом, чтобы встреча с убегающим происходила на эллипсе. Убегающий (цель) стартует из точки с координатами (0,0) и движется с постоянной скоростью ve под выбранным углом α. Преследователь двигается из точки (0,–m) и может управлять как углом направления перемещения β, так и скоростью vp > ve в пределах заданных ограничений, так, чтобы встреча состоялась на границе эллипса (рис. 2).
Расстояние от преследователя и убегающего до точки встречи 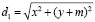 ,
, 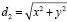 .
.
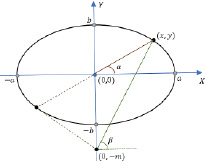
Рис. 2. Пример задачи преследования-убегания при встрече игроков на эллипсе
Преследователь осуществляет управление скоростью и углом, таким образом, имеем следующую систему уравнений:
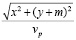 =
= 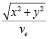 – время до встречи преследователя и убегающего,
– время до встречи преследователя и убегающего,
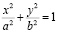 – уравнение эллипса с центром в точке (0,0),
– уравнение эллипса с центром в точке (0,0),
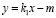 – уравнение линии, по которой происходит преследование,
– уравнение линии, по которой происходит преследование,
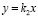 – уравнение линии, по которой происходит преследование.
– уравнение линии, по которой происходит преследование.
При этом коэффициент k2 задается самим убегающим, a,b считаются известными на момент решения задачи. Неизвестными являются k1 и vp, т.е. параметры преследователя.
Решение разобьем на следующие этапы:
1. Найдем пересечение линии убегания с эллипсом из указанной системы уравнений. После подстановки y = k2x получим
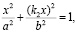 (6)
(6)
откуда
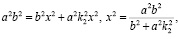
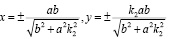
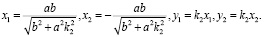
2. Найдем время пересечения убегающим границы эллипса и направление движения преследователя.
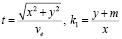 (7)
(7)
3. Найдем скорость, которой должен обладать преследователь при найденном месте встречи и известной скорости убегающего.
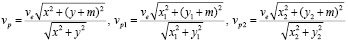 (8)
(8)
Соотношение скоростей в задаче преследования-убегания должно составлять
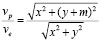 (9)
(9)
Таким образом, найдены все необходимые параметры задачи преследования. Динамическая задача, связанная с варьированием направления движения убегающим, решается на практике применением стратегии параллельного сближения.
Результаты исследования и их обсуждение
Пример 1. Рассмотрим в качестве примера передаточную функцию продольного движения летательного аппарата (ЛА)
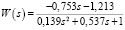 (10)
(10)
Для замкнутой системы:
Wз(S)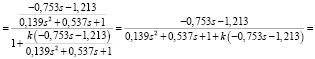
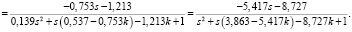
Покажем наличие инвариантов по отношению к статической обратной связи. Запишем коэффициенты передаточных функций Q0(p) и Q1(p) в виде матриц
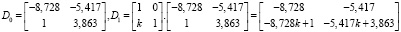 .
.
Таким образом, имеем инварианты:
1) элементы первых строк матриц D0 и D1: –8,728, –5,417;
2) матрица 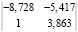 .
.
Указанные характеристики динамических систем остаются неизменными, т.е. являются инвариантами к рассмотренному преобразованию Q1(p). Все остальные инварианты статической обратной связи могут быть выражены через эти величины.
Пример 2. В качестве второго примера рассмотрим решение задачи преследования-убегания при указанной ранее постановке. Введем отношение осей эллипса как n = b / a, 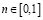 и примем без потери общности, что a = 1,
и примем без потери общности, что a = 1, 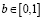 ,тогда получим
,тогда получим
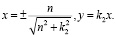 (11)
(11)
При этом 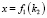 ,
, 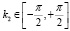 .
.
Построим график зависимости (рис. 3) скорости преследователя c начальным положением (0, –0,5) при фиксированной скорости ve = 5 и направлении k2 = π / 4 убегающего от параметров эллипса vp = f2(n).
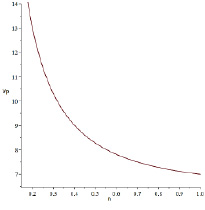
Рис. 3. Зависимость скорости преследователя от параметров эллипса
Таким образом, полученное решение позволяет, управляя скоростью преследователя, приводить к встрече на границе эллипса с заранее заданными коэффициентами при движении убегающего игрока с постоянной скоростью в произвольном направлении. Это в некотором смысле обратная задача управления, у которой все решения лежат на границе эллипса, который служит инвариантом при фиксированных параметрах движения убегающего.
Результаты проведенных исследований могут быть использованы при решении ряда задач, связанных с управлением движения летательных аппаратов (ЛА). В том числе:
1. Результаты в части выявления инвариантных показателей передаточных функций замкнутых систем управления ЛА могут быть использованы для обеспечения устойчивости широкого класса устройств.
2. Результаты в части построения устойчивых эллиптических границ встречи двух ЛА имеют прикладное значение для решения задач стыковки объектов на эллиптической орбите и решения дифференциальной игры преследования-уклонения в задачах двойного назначения в условиях территориальных ограничений.
На рис. 4 показан пример иллюстрации двух задач, когда убегающий движется из точки (0,0) под углами α и α*, а преследователь движется из точки (0, –m), так чтобы встреча состоялась в первом варианте на границе эллипса, а во втором варианте на границе окружности. Площадь, охватываемая окружностью So = πr2, площадь эллипса Sэ = πab, где a и b соответственно, длина большой и малой полуоси, a ≥ b.
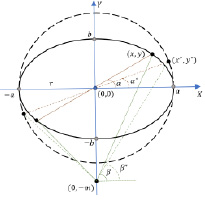
Рис. 4. Пример задачи преследования-убегания при встрече игроков на эллипсе и на окружности
Положим a = r, тогда соотношение площадей, охватываемых кругом и эллипсом, составляет
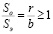 ,
,
что определяет поиск решения в ограниченной области возможной встречи ЛА.
Заключение
В настоящей работе рассмотрены некоторые способы применения инвариантов в технических системах. Показаны инварианты передаточных функций для систем автоматического управления. В качестве геометрического инварианта для расчета места встречи преследователя и убегающего рассмотрен эллипс. Эллиптическая форма границы встречи преследователя и убегающего является более общей по отношению к окружности. Возможным преимуществом предлагаемого подхода является сужение области решения задачи преследования-убегания в случае, например, наличия естественного территориального ограничения. В дальнейшем задача поиска инвариантов в системах управления может иметь расширение. Так, например, планируется рассмотреть передаточные функции более высоких порядков. Для трехмерного случая дифференциальной игры преследования-убегания в качестве инварианта предлагается рассмотреть эллипсоид, который ограничивает область реализуемых значений управления.
Работа выполнена при финансовой поддержке проекта РФФИ № 20-07-00022 А «Разработка и исследование методов распознавания образов на основе инвариантов к яркостным и геометрическим преобразованиям в системах технического зрения беспилотных летательных аппаратов».



